Решение прикладных задач методом дихотомии
СОДЕРЖАНИЕ: Кафедра информатики и вычислительной информатики Дисциплина «ИНФОРМАТИКА» ОТЧЕТ по курсовой работе Тема: «Решение прикладных задач методом дихотомии »Кафедра
информатики и вычислительной информатики
Дисциплина «ИНФОРМАТИКА»
ОТЧЕТ
по курсовой работе
Тема: «Решение прикладных задач методом дихотомии »
Москва 2009 г.
ЗАДАНИЕ НА КУРСОВУЮ РАБОТУ
Вариант № 11.
Часть 1
Использование численных методов решения нелинейных уравнений , используемых в прикладных задачах.
Для выполнения 1 части необходимо:
· Составить программу и рассчитать значение функции в левой части нелинейного уравнения для решения задачи отделения корней;
· Составить логическую схему алгоритма, таблицу идентификаторов и программу нахождения корня уравнения методом дихотомии и методом Ньютона ;
· Ввести программу в компьютер ,отладить, решить задачу с точностью =0.0001 и вывести результат;
· Предусмотреть в программе вывод на экран дисплея процесса получения корня.
Уравнение: 
, [1,2];
Метод численного решения: метод дихотомии,метод хорд.
Решение.
Метод дихотомии
1.
Этот метод позволяет отыскать корень уравнения f(
)=0 с любой наперед заданной точностью .
Предполагается,что искомый корень уравнения уже отделен,т.е. указан отрезок [ a ; b ] непрерывности функции f(x) такой,что на концах этого отрезка функция принимает различные значения.
Суть метода в том, что [ a ;b ] делится пополам.Половина, где нет корня отбрасывается, а другая делиться на два.
1-й Шаг. Вычисление середины отрезка
Если
f(
)=0, то мы нашли точный корень уравнения.
Если
f(
) · f(x0)0, то находится в интервале [
] следовательно 
; 
Иначе
2-й Шаг. Вычисление середины отрезка
Если
f(
)=0, то мы нашли точный корень уравнения.
Если
f(
· f(x1
)0 , то 
; 
Иначе
n -ый Шаг. Вычисление середины отрезка
Если
f(
)=0, то мы нашли точный корень уравнения.
Если
f(
·f(xn
)0 , то 
; 
Иначе
Условием нахождения корня является:
2. Нелинейное уравнение и условие его решения:
, [1,2], = 0,0001;
3. График функции:
4. Схема алгоритма:
 |
||||
 |
||||
 |
||||
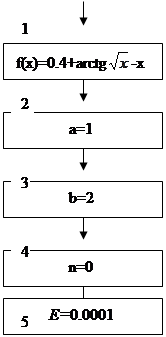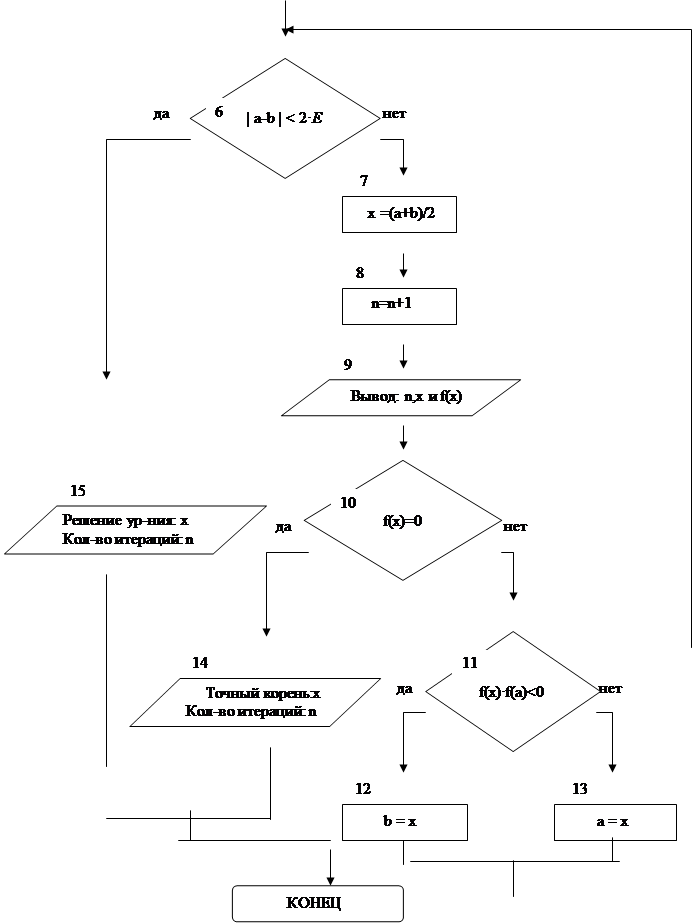5. Таблица идентификаторов:
| Обозначение | Идентификатор | Тип |
| n | n | int |
 |
a | double |
 |
b | double |
 |
eps | double |
| x | x | double |
| f(x) | f(x) | double |
6. Листинг программы :
#includestdio.h
#includemath.h
double f(double x)
{
return 0.25*(pow(x,3))+x-1.2502;
}
int main(void)
{
int n=0;
double x,a=0.,b=2.,eps=0.0001;
while (fabs(a-b)2*eps)
{
x=(a+b)/2,
n++;
printf(step=%3i x=%11.8lf f(x)=%11.8lf\n,n,x,f(x));
if (f(x)==0)
{
printf(Tothnii koreni x=%lf\nkolithestvo iteratsii n=%i\n,x,n);
return 0;
}
else if (f(a)*f(x)0) b=x;
else a=x;
}
printf(Reshenie x=%11.8lf pri Eps=%lf\nkolithestvo iteratsii n=%i\n,x,eps,n);
return 0;
}
7. Листинг решения:
step= 1x= 1.50000000f(x)=-0.21392288
step= 2x= 1.25000000f(x)=-0.00893133
step= 3x= 1.12500000f(x)= 0.08982692
step= 4x= 1.18750000f(x)= 0.04080796
step= 5x= 1.21875000f(x)= 0.01602415
step= 6x= 1.23437500f(x)= 0.00356738
step= 7x= 1.24218750f(x)=-0.00267680
step= 8x= 1.23828125f(x)= 0.00044659
step= 9x= 1.24023438f(x)=-0.00111478
step= 10 x= 1.23925781f(x)=-0.00033401
step= 11 x= 1.23876953f(x)= 0.00005631
step= 12 x= 1.23901367f(x)=-0.00013885
step= 13 x= 1.23889160f(x)=-0.00004127
Reshenie x= 1.23889160 pri Eps=0.0001
kolithestvo iteratsii n=13
Метод хорд:
1. Этот метод заключается в том, что к графику функции проводится хорда. Находим точку пересечения с осью OX и опускаем из этой точки прямую параллельную OY. Из точки пе-ресечения прямой и графика проводим хорду и операция повторяется до тех пор, пока точка пересечения хорды с осью OX не приблизиться к корню функции до заданной погрешности.
Шаг первый:
Нас интересует точка пересечения с осью ОХ.
Сделаем допущение: х=x1
y=0
Введем обозначение
x0
f()=f(x0
)
Подставим в уравнение
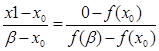
Отсюда
x1=x0
-
Шаг второй:
x2=x1-
Для n -го шага:
xn
=xn
-1
-
Условием нахождения корня является:
2. Нелинейное уравнение и условие его решения:
, [1,2], = 0,0001;
3. График функции:
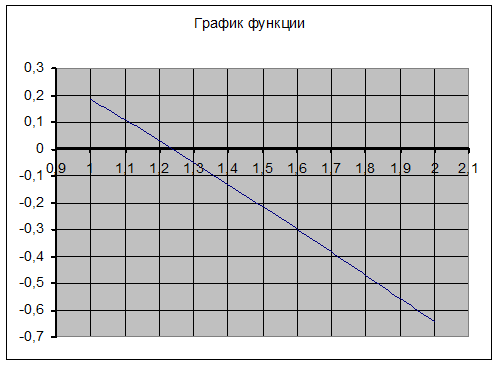
Таблица идетификаторов:
| Обозначение | Идентификатор | Тип |
| n | n | int |
|
a | double |
|
b | double |
|
eps | double |
| x | x | double |
| f(x) | f(x) | double |
6. Листинг программы :
#includestdio.h
#includemath.h
double f(double x)
{
return (0.25*(pow(x,3)))+x-1.2502;
}
int main(void)
{
int n=0;
double x,a=1.,b=2.,eps=0.0001,xn;
xn=a;
while (fabs(xn-x)eps)
{
x=xn;
n++;
xn=x-f(x)*(b-x)/(f(b)-f(x));
printf(step=%3i x=%11.8lf f(x)=%11.8lf\n,n,xn,f(xn));
}
printf(pribligennoe znathenie x=%lf pri Eps=%lf\nkolithestvo iterasii n=%i\n,xn,eps,n);
return 0;
}
7. Листинг решения:
step= 1 x= 1.22334934 f(x)= 0.01236182
step= 2 x= 1.23796144 f(x)= 0.00070219
step= 3 x= 1.23879055 f(x)= 0.00003951
step= 4 x= 1.23883720 f(x)= 0.00000222
pribligennoe znathenie x=1.238837 pri Eps=0.0001
kolithestvo iterasii n=4
Анализ результатов:
| метод дихотомии | метод хорд | |
| значение корня | 1.23889160 | 1.23883720 |
| значение функции | -0.00004127 | 0.00000222 |
| количество итераций | 13 | 4 |
Вывод: Метод дихотомии прост в реализации, но обладает малой скоростью сходимости по сравнению с методом хорд, что выражается в количестве шагов. Метод хорд к тому же обладает большей точностью.
Часть 2
Решение дифференциального уравнения.
Вариант №11.
Метод Эйлера
1.Математическое описание
Геометрический смысл метода Эйлера состоит в следующем: дифференциальное уравнение определяет в точке (x0 ,y0 ) направление касательной к искомой интегральной кривой
k 0 = y ( x 0 )= f ( x 0 , y 0 )
Отрезок интегральной кривой, соответствующий x
(
x
0
,
x
1
)
, x
1
=
x
0
+
h
заменяется участком касательной с угловым коэффициентом k
. Найденная точка (
x
1
,
y
1
)
используется в качестве нового начального условия для уравнения y
(
x
1
)=
y
1
,
в ней вновь вычисляется угловой коэффициент поля направлений и процедура повторяется.
На n-ом шаге имеем точку (xn -1 ,yn -1 ), задающую начальное условие для уравнения:
y ( xn -1 )= yn -1
Уравнение определяет угловой коэффициент касательной к интегральной кривой в этой точке
Соответствующее уравнение касательной:y - yn -1 = k ( x - xn -1 )
Отсюда получаем значение х=хn , соответствующее точке: х n =х n -1 + h ,
А именно: yn - yn -1 = kn -1 ( xn -1 + h - xn -1 ), или
yn =yn-1 +h·kn-1
yn =yn-1 +h·f(xn-1, yn-1 )
Полученная формула является основной расчетной формулой метода Эйлера.
Процесс вычислений заканчивается, когда аргумент после очередного приращения выйдет за пределы исследуемого отрезка 
.
2. Дифференциальное уравнение:
x0
= 0 , y0
= 1, xmax
=1, x = 0.01; 0.005; 0.001
3. Схема алгоритма:
 |
|||||||
 |
|||||||
 |
|||||||
 |
|||||||
 |
|||||||
 |
|||||||
5. Таблица идентификаторов:
| Обозначение | Идентификатор | Тип |
| s | s | int |
| i | i | int |
| x | x | double |
| xmax | x_max | double |
| x1 | x1 | double |
x |
h[i] | double |
| y | y | double |
| d | d | double |
| f(x) | f(x) | double |
| k | k(x,y) | double |
6. Листинг программы:
#includestdio.h
#includemath.h
double k(double x,double y )
{
return ((x/exp(x*x))-2.*x*y);
}
double f(double x)
{
return ((1./exp(x*x))*(1+x*x/2.));
}
int main(void)
{
int s,i;
double x,x1,x_max=1,y,d;
double h[3]={0.01,0.005,0.001};
FILE*file;
file=fopen(result.txt,w+);
for (i=0;i=2;i++)
{ s=0;y=1;
fprintf(file,h(%i)=%lf\n,i,h[i]);
for(x=0;x=x_max;x+=h[i])
{
s++;
x1=x+h[i];
y=y+k(x,y)*h[i];
d=y-f(x1);// y- pribl. f(x)- tochnoe
printf( step =%4.i x=%6.4lf y=%6.4lf yt=%6.4lf d=%10.8lf\n,s,x1,y,f(x1),d);
fprintf(file, step =%4.i x=%10.8lf y=%10.8lf yt=%10.8lf d=%10.8lf\n,s,x1,y,f(x1),d);
}
}
fclose(file);
return 0;
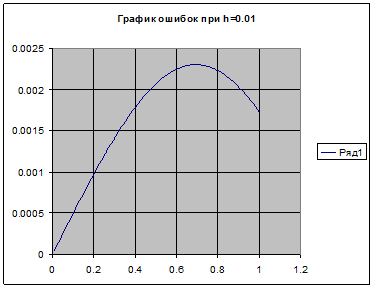
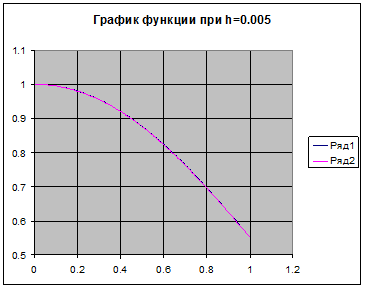
Вывод: Интегрированная среда Visual С позволяет обрабатывать программы ,записанные на языке С++ .Для программирования циклических алгоритмов были использованы операторы организации циклов с параметрами, решение использует форматируемый вывод и оператор присваивания, а также использовались операторы вызова функций. Чем больше шаг, тем точнее вычисления.