Решение вариационной задачи путем сведения к задаче нелинейного программирования
СОДЕРЖАНИЕ: Домашнее задание по курсу Статистические методы обработки информации на тему: Решение вариационной задачи путем сведения к задаче нелинейного программированияДомашнее задание
по курсу Статистические методы обработки информации на тему:
Решение вариационной задачи путем сведения к задаче нелинейного программирования
Выполнила студентка
Преподаватель
Москва, 2006
Вариант № 7 .
Уравнение объекта имеет вид: ![]() .
.
Модель объекта: ![]()
Шум измерений принадлежит классу, удовлетворяющему условию:
![]() .
.
Распределение ![]() является нормальным распределением :
является нормальным распределением :
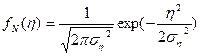 .
.
Распределение ![]() тоже является нормальным распределением с произвольной дисперсией
тоже является нормальным распределением с произвольной дисперсией ![]() :
:
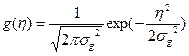 .
.
1. Получить нормированную информационную матрицу, соответствующую данному объекту.
2. Допуская, что оптимальная на классе плотность распределения существует, разработать алгоритм определения оптимальной на классе плотности распределения ![]() (функции потерь). Для определения оптимальной на классе плотности распределения используется N измерений «входов» и «выходов».
(функции потерь). Для определения оптимальной на классе плотности распределения используется N измерений «входов» и «выходов».
3. Записать рекуррентный алгоритм с использованием оптимальной на классе функции потерь.
В дальнейшем будем использовать запись объекта в виде:
![]() .
.
Модель выглядит следующим образом:
![]() ,
,
где ![]() ,
, ![]() .
.
Тогда:
![]()
1. Определение нормированной информационной матрицы
Уравнение объекта: ![]() .
.
Уравнение модели: ![]() ,
, ![]()
Нормированной информационной матрицей называется матрица вида:
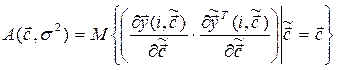 , где
, где
![]() .
.
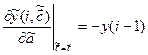
![]()
Три последних слагаемых равны нулю, так как фигурирующие в них величины не коррелированны. Кроме того, матрицу вычисляем для стационарного процесса, значит, значения выхода в каждый момент времени одинаковы, поэтому индексы при у опустим. Следовательно, наша формула примет вид:
![]() , откуда
, откуда
![]() .
.
Перейдем ко второй компоненте вектора параметров объекта:
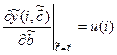 .
.
Значит, для стационарного процесса ![]() .
.
Заметим также, что
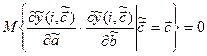 .
.
Тогда нормированная информационная матрица:
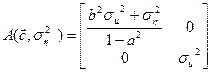 ,
,
Обратная ей:
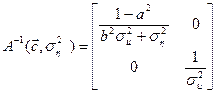 ,
,
а след обратной матрицы вычисляется по формуле:
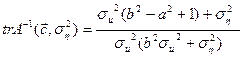 .
.
2. Поиск оптимальной на классе функции потерь
Теоретические сведения
Как правило, при неполной информации о помехе можно выделить тот или иной класс распределений, которому принадлежит распределение помехи ![]() . При этом можно сформировать соответствующий класс функций потерь Q
:
. При этом можно сформировать соответствующий класс функций потерь Q
:
![]() , где
, где ![]() .
.
При нахождении требуемой функции потерь используется игровой подход. Причем в качестве «платы» рассматривается АМКО.
В общем случае, искомая функция потерь, гарантирующая некоторую максимальную АМКО, является решением задачи:
![]() , (1)
, (1)
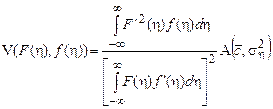 , (2)
, (2)
![]() ,
, ![]() . (3)
. (3)
Данная задача является сложной вариационной задачей с ограничениями (3). В настоящее время не существует каких-либо разработанных методов решения поставленной задачи в явном виде. Можно представить только численное решение.
Существенное упрощение задачи достигается, если существует оптимальная функция потерь:
![]() ,
, ![]() .
.
Определение.
Функция потерь ![]() , где
, где ![]() , существует и называется оптимальной на классе F, если для нее выполняется условие:
, существует и называется оптимальной на классе F, если для нее выполняется условие:
![]() ,
,
![]() ;
;
для ![]() ,
, ![]() .
.
Оптимальная на классе функция потерь обладает двумя свойствами.
Свойство 1.
Оптимальная на классе плотность распределения ![]() и соответствующая ей функция потерь
и соответствующая ей функция потерь ![]() определяют седловую точку.
определяют седловую точку.
Свойство 2. Оптимальная на классе плотность распределения является наименее благоприятной плотностью распределения.
Таким образом, если заранее известно, что оптимальная функция потерь существует, то на основании свойства 1 можно записать:
![]() ,
,
где, на основании свойства 2,
![]() .
.
Таким образом, задача (1) эквивалентна задаче:
![]() ;
;
![]() , (4)
, (4)
где
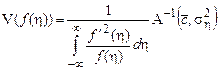 . (5)
. (5)
Последнюю задачу можно упростить, если принять во внимание, что для целей идентификации важна не сама АМКО, а ее диагональные элементы. Учитывая это, рационально перейти к рассмотрению следа АМКО. Тогда задача (4) примет вид:
![]()
или, подставляя выражение для ![]() ,
,
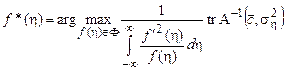 . (6)
. (6)
Переходя от задачи максимизации к более привычной задаче минимизации, окончательно получим:
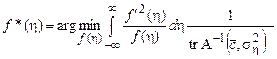 ,
, ![]() . (7)
. (7)
Несмотря на существенное упрощение, задача (7) является сложной вариационной задачей с нелинейными ограничениями, которая имеет явное решение только в частных случаях. В общем виде эта задача может быть решена только численно путем сведения ее к многомерной задаче нелинейного математического программирования.
Преобразование задачи (7) к задаче нелинейного программирования осуществляется за счет аппроксимации непрерывной ![]() кусочно-постоянной финитной функцией
кусочно-постоянной финитной функцией ![]() .
.
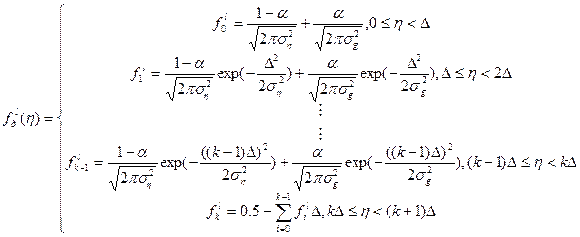 (8)
(8)
Причем, так как ![]() - четная, то можно проводит аппроксимацию только для положительных
- четная, то можно проводит аппроксимацию только для положительных ![]() , при этом интегралы заменяются суммами, а производные – разностями.
, при этом интегралы заменяются суммами, а производные – разностями.
Минимизируемая функция принимет вид:
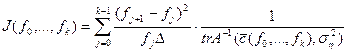 , (9)
, (9)
![]() ,
,
где - интервал разбиения.
Ограничения, накладываемые на ![]() определяются классом
определяются классом ![]() , обязательным же ограничением является условие:
, обязательным же ограничением является условие:
![]() ,
,
которое является дискретным аналогом условия:
![]()
Характерной особенностью задачи минимизации функции (7) является необходимость определения ![]() на каждом шаге итерационного процесса минимизации.
на каждом шаге итерационного процесса минимизации.
Но можно преобразовать задачу (7) к задаче нелинейного программирования и за счет вариации неизвестных параметров. Так как плотность распределения должна удовлетворять требованию:
![]() ,
,
то в ходе поиска оптимальной на классе функции потерь будем минимизировать функцию ![]() по
по ![]() при соблюдении ограничения.
при соблюдении ограничения.
Приведем постановку задачи минимизации к общему виду.
Найти минимум функции: ![]()
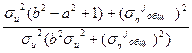
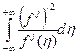
при ограничениях: ![]()
![]() ,
,
причем ![]() , а
, а
![]()
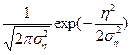 +
+ ![]()
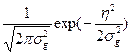 .
.
Общая схема процесса нахождения оптимальной на классе плотности распределения (функции потерь) может быть представлена блок-схемой.
Минимизация критерия J1 (f) решается одномерным методом «золотого» сечения. Критерий J1 (f) содержит в себе исходный критерий и дополнительное слагаемое, которое обращается в нуль при выполнении ограничения:
![]()
3. Рекуррентный алгоритм с использованием оптимальной на классе функции потерь
Так как пункт 2 был реализован в предположении, что оптимальная на классе функция потерь существует, то результатом работы описанных алгоритмов будет функция ![]() , соответствующая оптимальной
, соответствующая оптимальной ![]() .
.
Запишем для этой функции рекуррентный алгоритм.
Функция потерь: ![]() .
.
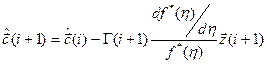 при условии, что
при условии, что ![]() ;
;
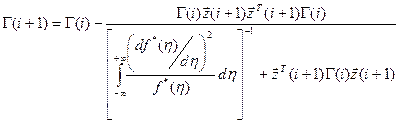 .
.
Заключение
В данной работе проводилась разработка алгоритма определения оптимальной на классе плотности распределения (функции потерь) при допущении, что она существует.
В ходе выполнения работы была рассчитана нормированная информационная матрица для заданного вида объекта. Разработанный алгоритм основан на сведении вариационной задачи к задаче нелинейного программирования. Задача нелинейного программирования решалась методом «золотого» сечения.