Решение задач по курсу теории вероятности и математической статистики
СОДЕРЖАНИЕ: Определение вероятности наступления определенного события по законам теории вероятности. Вычисление математического ожидания, дисперсии и среднего квадратичного отклонения. Нахождение выборочного уравнения регрессии по данным корреляционной таблицы.Вариант 1
№ 1
Три стрелка делают по одному выстрелу по одной и той же цели. Вероятности поражения целей равны соответственно р1 = 0,9, р2 = 0,8, р3 = 0,7.
Найти вероятности того, что:
а) все три стрелка попадают в цель;
б) только один из них попадает в цель;
в) хотя бы один стрелок попадает в цель.
Обозначим события: А – все 3 стрелка попадают в цель; В – только один стрелок попадает в цель; С – хотя бы один стрелок попадает в цель.
Вероятности промахов равны соответственно: q1 = 0,1, q2 = 0,2, q3 = 0,3.
а) Р(А) = р1 р2 р3 = 0,90,80,7 = 0,504.
б) Р(В) = p1 q2 q3 + q1 p2 q3 + q1 q2 p3 = 0,90,20,3 + 0,10,80,3 + 0,10,20,7 = 0,092.
в) Событие ![]() – все три стрелка промахиваются. Тогда
– все три стрелка промахиваются. Тогда
Р(С) = 1 – Р(![]() ) = 1 – 0,10,20,3 = 1 – 0,006 = 0,994.
) = 1 – 0,10,20,3 = 1 – 0,006 = 0,994.
№ 11
Вероятность наступления события в каждом из одинаковых независимых испытаний равна 0,02. Найти вероятность того, что в 150 испытаниях событие наступит ровно 5 раз
У нас nдостаточно велик, р мал, = np = 150 0,02 = 3 9, k = 5. Справедливо равенство Пуассона: ![]() . Таким образом,
. Таким образом, ![]()
№ 21
По данному закону распределения дискретной случайной величины Х определить математическое ожидание М(Х), дисперсию D(X) и среднее квадратическое отклонение (Х).
| хі | 1 | 2 | 3 | 4 | 5 |
| рі | 0,05 | 0,18 | 0,23 | 0,41 | 0,13 |
Последовательно получаем:
5
М(Х) = хі рі = 0,05 + 20,18 + 30,23 + 40,41 + 50,13 = 3,39.
i=1
5
D(X) = xi pi – M = 0,05 + 20,18 + 30,23 + 40,41 + 50,13 – 3,39 = i=1
1,1579.
![]()
![]() (Х) = D(X) = 1,1579 = 1,076.
(Х) = D(X) = 1,1579 = 1,076.
№ 31
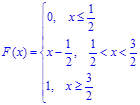
Случайная величина Х задана интегральной функцией
а) дифференциальную функцию f(x) (плотность вероятности);
б) математическое ожидание и дисперсию величины х;
в) вероятность того, что X примет значение, принадлежащее интервалу
![]() ;
;
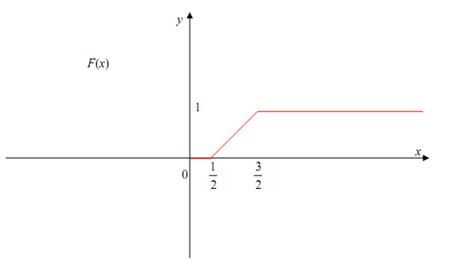
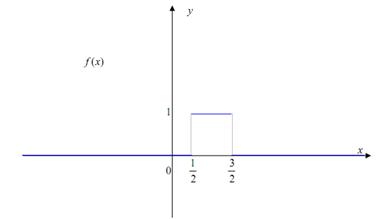
г) построить графики функций F(x) и f(x).
Последовательно получаем:
а)  ;
;
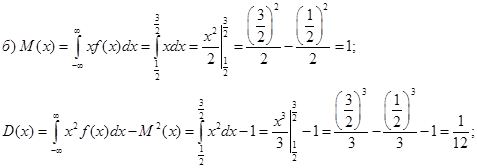
в) Р(a x b) = F(b) – F(a) P![]() = F(1) – F
= F(1) – F![]() =
= ![]() – 0 =
– 0 = ![]() .
.
Графики функций поданы далее.
№ 41
Определить вероятность того, что нормально распределённая величина Х примет значение, принадлежащее интервалу (; ) если известны математическое ожидание а и среднее квадратическое отклонение . Данные: = 2; = 13; а = 10; = 4.
Используем формулу Р( x ) = ![]()
Имеем: Р(2 x 13) =![]() = Ф
= Ф![]() – Ф(–2).
– Ф(–2).
Поскольку функция Лапласа есть нечетная, можем записать:
Ф![]() – Ф(–2) = Ф
– Ф(–2) = Ф![]() + Ф(2) = 0,2734 + 0,4772 = 0,7506.
+ Ф(2) = 0,2734 + 0,4772 = 0,7506.
№ 51
Поданному статистическому распределению выборки
| хі | 4 | 5,8 | 7,6 | 9,4 | 11,2 | 13 | 14,8 | 16,6 |
| mі | 5 | 8 | 12 | 25 | 30 | 20 | 18 | 6 |
Определить: а) выборочную среднюю; б) выборочную дисперсию;в) выборочное среднее квадратическое отклонение.
Для решения задачи введём условную переменную
![]() , где С – одно из значений хі
, как правило, соответствующее наибольшему значению mі
, а h– это шаг (у нас h = 1,8).
, где С – одно из значений хі
, как правило, соответствующее наибольшему значению mі
, а h– это шаг (у нас h = 1,8).
Пусть С = 11,2. Тогда ![]() .
.
Заполним таблицу:
| xi | mi | xi | xi mi | (xi )mi |
| 4 | 5 | – 4 | – 20 | 80 |
| 5,8 | 8 | – 3 | – 24 | 72 |
| 7,6 | 12 | – 2 | – 24 | 48 |
| 9,4 | 25 | – 1 | – 25 | 25 |
| 11,2 | 30 | 0 | 0 | 0 |
| 13 | 20 | 1 | 20 | 20 |
| 14,8 | 18 | 2 | 36 | 72 |
| 16,6 | 6 | 3 | 18 | 54 |
| = 124 | = – 19 | = 371 |
Используя таблицу, найдём  ;
;
![]() D(x) = (xi
)mi
– (xi
) =
D(x) = (xi
)mi
– (xi
) = ![]() – (– 0,1532) = 2,9685.
– (– 0,1532) = 2,9685.
Теперь перейдем к фактическим значениям х и D(x):
_
x = xh + C = – 0,15321,8 + 11,2 = 10,9242;D(x) =D(x)h = 2,96851,8 = 9,6178;
![]()
![]() (x) = D(x) = 9,6178 = 3,1013.
(x) = D(x) = 9,6178 = 3,1013.
№ 61
По данной корреляционной таблиценайти выборочное уравнение регрессии.
| у х | 6 | 9 | 12 | 15 | 18 | 21 | ny |
| 5 | 4 | 2 | 6 | ||||
| 15 | 5 | 23 | 28 | ||||
| 25 | 18 | 44 | 5 | 67 | |||
| 35 | 1 | 8 | 4 | 13 | |||
| 45 | 4 | 2 | 6 | ||||
| nx | 4 | 7 | 42 | 52 | 13 | 2 | n= 120 |
Для упрощения расчетов введем условные переменные
u = ![]() , v =
, v = ![]() .Составим таблицу:
.Составим таблицу:
| vu | – 3 | – 2 | – 1 | 0 | 1 | 2 | nv | nuv uv |
| – 2 | 4 6 | 2 4 | 6 | 32 | ||||
| – 1 | 5 2 | 23 1 | 28 | 33 | ||||
| 0 | 18 0 | 44 0 | 5 0 | 67 | 0 | |||
| 1 | 1–1 | 8 0 | 4 1 | 13 | 3 | |||
| 2 | 4 2 | 2 4 | 6 | 16 | ||||
| nu | 4 | 7 | 42 | 52 | 13 | 2 | n = 120 | = 84 |
Последовательно получаем:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]()
![]() u
=
u
= ![]() – (u) = 1,058 – (– 0,425) = 0,878; u
= 0,878= 0,937;
– (u) = 1,058 – (– 0,425) = 0,878; u
= 0,878= 0,937;
![]()
![]() v
=
v
= ![]() – (v) = 0,742 – (– 0,125) = 0,726; v
= 0,726 = 0,8521;
– (v) = 0,742 – (– 0,125) = 0,726; v
= 0,726 = 0,8521;
По таблице, приведённой выше, получаем nuv uv = 84.
Находим выборочный коэффициент корреляции:
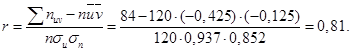
Далее последовательно находим:
x= uh1 + C1 = – 0,4253 + 15 = 13,725; y = vh2 + C2 = – 0,12510 + 25 = 23,75;
x = u h1 = 0,9373 = 2,811; y = v h2 = 0,852110 = 8,521.
Уравнение регрессии в общем виде:  Таким образом,
Таким образом,
![]() упрощая, окончательно получим искомое уравнение регрессии:
упрощая, окончательно получим искомое уравнение регрессии: ![]()
Необходимо произвести проверку полученного уравнения регрессии при, по крайней мере, двух значениях х.
1) при х = 12 по таблице имеем
![]()
по уравнению:
ух=12 = 2,45712 – 9,968 = 19,516; 1 = 19,762 – 19,516 = 0,246;
2) при х = 18 по таблице имеем
![]()
по уравнению:
ух=18 = 2,45718 – 9,968 = 34,258; 2 = 34,258 – 34,231 = 0,027.
Отмечаем хорошее совпадение эмпирических и теоретических данных.
Вариант 2
№ 2
Для сигнализации об аварии установлены 3 независимо работающие устройства. Вероятности их срабатывания равны соответственно р1 = 0,9, р2 = 0,95, р3 = 0,85. Найти вероятности срабатывания при аварии:
а) только одного устройства;
б только двух устройств;
в) всех трёх устройств.
Обозначим события: А – срабатывает только одно устройство; В – срабатывают 2 устройства; С – срабатывают все 3 устройства. Вероятности противоположных событий (не срабатывания) соответственно равны q1 = 0,1, q2 = 0,05, q3 = 0,15. Тогда
а) Р(А) = p1 q2 q3 + q1 p2 q3 + q1 q2 p3 = 0,90,05 0,15 + 0,10,950,15 + 0,10,050,85 = 0,02525.
б) Р(В) = p1 p2 q3 + p1 q2 p3 + q1 p2 p3 = 0,90,950,15 + 0,90,050,85 + 0,10,950,85 = 0,24725.
в) Р(С) = р1 р2 р3 = 0,90,950,85 = 0,72675.
№ 12
В партии из 1000 изделий имеется 10 дефектных. Найти вероятность того, что из взятых наудачу из этой партии 50 изделий ровно 3 окажутся дефектными.
По условию ![]() n = 50, k = 3. Поскольку р мал, n достаточно большое, в то же время nр = 0,5 9, справедлива формула Пуассона:
n = 50, k = 3. Поскольку р мал, n достаточно большое, в то же время nр = 0,5 9, справедлива формула Пуассона:![]() .
.
Таким образом, ![]()
№ 22
По данному закону распределения дискретной случайной величины Х определить математическое ожидание М(Х), дисперсию D(X) и среднее квадратическое отклонение (Х).
| хі | 2 | 3 | 4 | 5 | 8 |
| рі | 0,25 | 0,15 | 0,27 | 0,08 | 0,25 |
Последовательно получаем:
5
М(Х) = хі рі = 20,25 + 30,15 + 40,27 + 50,08 + 80,25 = 4,43.
i=1
5
D(X) = xi
pi
– M = 20,25 + 30,15 + 40,27 +50,08 + 80,25 – 4,43 ![]() і=1
і=1
= 5,0451.
![]() (Х) = D(X) = 5,0451= 2,246.
(Х) = D(X) = 5,0451= 2,246.
№ 32
Случайная величина Х задана интегральной функцией
а) дифференциальную функцию f(x) (плотность вероятности);
б) математическое ожидание и дисперсию величины х;
в) вероятность того, что X примет значение, принадлежащее интервалу
![]() ;
;
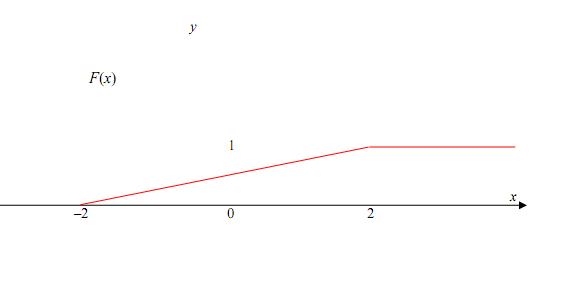
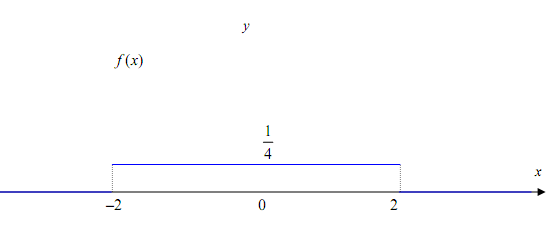
г) построить графики функций F(x) и f(x).
Последовательно получаем:
а)  ;
;

в) Р(a x b) = F(b) – F(a) P![]() = F(1) – F
= F(1) – F![]() =
= 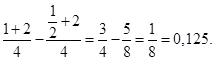
Графики функций приводятся далее.
![]()
![]()
№ 42
Определить вероятность того, что нормально распределённая величина Х примет значение, принадлежащее интервалу (;) если известны математическое ожидание а и среднее квадратическое отклонение . Данные: = 5; = 14; а = 9; = 5.
Используя формулу ![]() имеем
имеем
![]()
Поскольку функция Лапласа есть нечетная, можем записать:
![]()
№ 52
По данному статистическому распределению выборки
| хі | 7,6 | 8 | 8,4 | 8,8 | 9,2 | 9,6 | 10 | 10,4 |
| mі | 6 | 8 | 16 | 50 | 30 | 15 | 7 | 5 |
Определить: а) выборочную среднюю; б) выборочную дисперсию;в) выборочное среднее квадратическое отклонение.
Для решения задачи введём условную переменную ![]()
где С – одно из значений хі , как правило, соответствующее наибольшему значению mі , а h – это шаг (у нас h = 0,4).
Пусть С = 8,8. Тогда ![]()
Заполним таблицу:
| xi | mi | xi | xi mi | (xi )mi |
| 7,6 | 6 | – 3 | – 18 | 54 |
| 8 | 8 | – 2 | – 16 | 32 |
| 8,4 | 16 | – 1 | – 16 | 16 |
| 8,8 | 50 | 0 | 0 | 0 |
| 9,2 | 30 | 1 | 30 | 30 |
| 9,6 | 15 | 2 | 30 | 60 |
| 10 | 7 | 3 | 21 | 63 |
| 10,4 | 5 | 4 | 20 | 80 |
| = 137 | = 51 | = 335 |
Используя таблицу, найдём
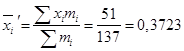 ;
;
![]() D(x) = (xi
)mi
– (xi
) =
D(x) = (xi
)mi
– (xi
) = ![]() – 0,3723 = 2,3067.
– 0,3723 = 2,3067.
Теперь перейдем к фактическим значениям х и D(x):
x = xh + C = 0,37230,4 + 8,8 = 8,9489; D(x) = D(x)h = 2,30670,4 = 0,3961;
![]()
![]() (x) = D(x) = 0,3961 = 0,6075.
(x) = D(x) = 0,3961 = 0,6075.
№ 62
По данной корреляционной таблице
| у х | 4 | 8 | 12 | 16 | 20 | 24 | ny |
| 10 | 2 | 5 | 7 | ||||
| 20 | 6 | 8 | 4 | 18 | |||
| 30 | 8 | 46 | 10 | 64 | |||
| 40 | 5 | 20 | 4 | 29 | |||
| 50 | 3 | 14 | 2 | 5 | 22 | ||
| nx | 2 | 19 | 62 | 48 | 6 | 3 | n = 140 |
найти выборочное уравнение регрессии.
Для упрощения расчетов введём условные переменные
![]() Составим таблицу.
Составим таблицу.
| – 2 | – 1 | 0 | 1 | 2 | 3 | nv | nuv uv | |
| – 2 | 2 4 | 5 2 | 7 | 18 | ||||
| – 1 | 6 1 | 8 0 | 4 –1 | 18 | 2 | |||
| 0 | 8 0 | 46 0 | 10 0 | 64 | 0 | |||
| 1 | 5 0 | 20 1 | 4 2 | 29 | 28 | |||
| 2 | 3 0 | 14 2 | 2 4 | 5 6 | 22 | 66 | ||
| nu | 2 | 19 | 62 | 48 | 6 | 3 | n = 140 | = 114 |
Последовательно получаем:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]()
![]() u
=
u
= ![]() – (u) = 0,9 – 0,329 = 0,792; u
= 0,792 = 0,89;
– (u) = 0,9 – 0,329 = 0,792; u
= 0,792 = 0,89;
![]()
![]() v
=
v
= ![]() – (v) = 1,164 – 0,293 = 1,079; v
= 1,079 = 1,0385;
– (v) = 1,164 – 0,293 = 1,079; v
= 1,079 = 1,0385;
По таблице, приведённой выше, получаем nuv uv = 114.
Находим выборочный коэффициент корреляции:
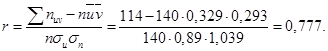
Далее последовательно находим:
x = uh1 + C1 = 0,3294 + 12 = 13,314; y = vh2 + C2 =0,29310 + 30 = 32,929;
x = u h1 = 0,894 = 3,56; y = v h2 = 1,038510 = 10,385.
Уравнение регрессии в общем виде:  Таким образом,
Таким образом,
![]() упрощая, окончательно получим искомое уравнение регрессии:
упрощая, окончательно получим искомое уравнение регрессии: ![]()
Необходимо произвести проверку полученного уравнения регрессии при, по крайней мере, двух значениях х.
1) при х = 12 по таблице имеем ![]()
по уравнению: ух=12 = 2,26612 + 2,752 = 29,944; 1 = 30,484 – 29,944 = 0,54;
2) при х = 16 по таблице имеем ![]()
по уравнению: ух=16 = 2,26616 + 2,752 = 39,008; 2 = 39,167 – 39,008 = 0,159.
Отмечаем хорошее совпадение эмпирических и теоретических данных.