Резисторы и конденсаторы в «полупроводниковом» исполнении. Топологические решения и методы расчета

СОДЕРЖАНИЕ: Резисторы, конденсаторы их суть понятие и характеристика. Полупроводниковое соединение резисторов и конденсаторов. Топологическое решение и методы расчета. Емкость конденсаторов типа металл — диэлектрик — полупроводник. Коэффициент паразитной емкости.

БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ

Кафедра ЭТТ

РЕФЕРАТ

На тему:

«Резисторы и конденсаторы в «полупроводниковом» исполнении. Топологические решения и методы расчета»

МИНСК, 2008

1. Конденсаторы

В качестве конденсаторов, т. е. пассивных элементов полупро­водниковых ИМС, предназначенных для использования их .емкос­ти, чаще всего находят применение обратно-смещенные р — п- gt реходы Кроме того, применяются структуры типа металл —ди­электрик .— полупроводник (МДП) (в том числе в биполярных микросхемах). Реже используются структуры типа металл — ди­электрик — металл (МДМ).

На рисунке 1.1 изображены структуры конденсаторов полупровод­никовых микросхем, а В таблице 1.1 представлены ориентировочныезначения их параметров

.

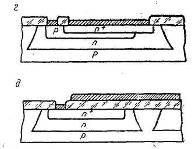
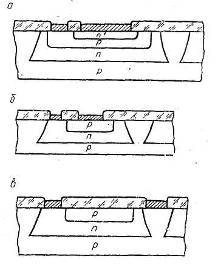
Рисунок 1.1. Структуры конденсаторов

полупроводниковых микросхем: а—на основе эмиттерного р—п -перехода транзистора; б—на основе коллекторного перехода: в - на основе р-n перехода кол­лектор—подложка; г-на основе парал­лельно включенных емкостей эмиттерного и коллекторного р— n-переходов; д— типа металл—диэлектрик—полупроводник.

Поскольку профиль распределения концентрации примесей в вертикальных (боковых) плоскостях пленарных р — n-переходов, полученных диффузией, значительно отличается от профиля рас­пределения в горизонтальной части р — n -переходов и аналитичес­кий расчет его затруднителен, В таблице приводятся ориентиро­вочные значения параметров для обоих случаев. Полная емкость.

Таблица 1.1

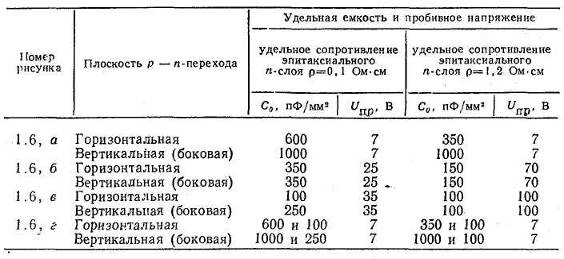
конденсатора при использовании данных Таблица рассчитывается в соответствии с соотношением

(1.1)

где С_огор , С_оверт и S_гор S_верт — удельные емкости и площади гори­зонтальных и вертикальных плоскостей р — «-переходов.

Температурный коэффициент емкости (ТКЕ) конденсатора оп­ределяется выражением

(1.2)

где Т — температура.

Если в интервале температур (Т₂ —Т₁ ) изменение емкости (С₂ — С₁ )связано с изменением температуры линейной зависи­мостью, то ТКЕ описывается формулой

(1.3)

Для конденсаторов на основе р—переходов при обратных на­пряжениях порядка нескольких вольт ТКЕ составляет величину а_с = (2—5) 10⁴ 1/град.

Емкость конденсаторов типа металл — диэлектрик — полупро­водник рассчитывается следующим образом. Поскольку полная удельная емкость структуры типа МДП С_о состоит из последова­тельно включенных удельных емкостей диэлектрика С_Од и прост­ранственного заряда в полупроводнике С_0П) она может быть опре­делена согласно соотношению:

(1.4)

Удельная емкость диэлектрика является величиной постоянной, определяет максимальную удельную емкость всей структуры и рассчитывается по формуле

(1.5)

Где и — диэлектрическая проницаемость и толщина диэлект­рической пленки.

Емкость области пространственного заряда в поверхностном слое полупроводника зависит от приложенного к МДП-конденсатору напряжения.

Если знак и величина приложенного напряжения таковы, что на поверхности полупроводника образуется слой, обогащенный ос­новными носителями заряда, полная удельная емкость определяет­ся удельной емкостью диэлектрика, т. е. С₀ =С_0я . (Для структуры, изображенной на рисунке 1.1, д, это равенство будет выполняться при приложении к металлическому электроду, расположенному над окислом, достаточно большого по величине напряжения положи­тельного знака.)

При соответствующих знаке и достаточно большой величине при­ложенного напряжения в приповерхностном слое полупроводника под окислом может образоваться инверсионный слой, т. е. слой с обратной по отношению к нейтральному состоянию полупроводни­ка проводимостью. В условиях сильной инверсии удельная емкость пространственного заряда С_ов постоянна и может быть рассчитана так же, как емкость p—n перехода.

В условиях, промежуточных по отношению к описанным двум экстремальным случаям, полная удельная емкость МДП-конденсатора рассчитывается согласно соотношению

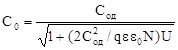(1.6)

где N — концентрация примесей в полупроводнике; U — приложен­ное напряжение.

Рассмотренная зависимость емкости МДП-конденсатора на частотах выше 100 Гц от напряжения (вольт-фарадная характерис­тика) иллюстрируется Рисунок 3.1.2. Как видно из рисунка, при отрица­тельных напряжениях на металлическом электроде (для полупро­водника р-типа) удельная емкость определяется емкостью окисла, при значительных положительных на­пряжениях — емкостью простран­ственного заряда инверсионного слоя в полупроводнике, при проме­жуточных значениях напряжения она изменяется согласно соотношению (1.5).

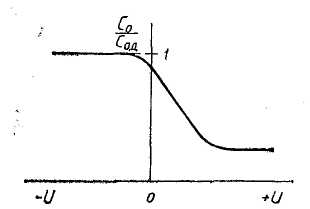
Рисунок 1.2 Зависимость нормализо­ванной удельной емкости МДП-конденсатора от величины и зна­ка приложенного напряжения.

Ориентировочно структура типа МДП- (см. Рисунок 1.1, д) обладает ванной удельной емкости С₀ =400 — 600 пФ/мм² и пробивным напряжением U_пр =10—50 В. ТКЕ составляет величину около а_с =10^-4 1/град. Конденсаторы, как правило, не применяются в современных логических ИМС. В аналоговых микросхемах находят применение конденсаторы на основе р —«-переходов и иногда — в виде структур типов МДП или МДМ. В запоминающих устройствах (ЗУ) широко используются емкости р—n-переходов и МДП-структур.

2. Резисторы

В качестве резисторов, т. е. пассивных элементов ИМС, пред­назначенных для использования их электрического сопротивления, применяются обычно слои полупроводника, создаваемые с помощью диффузии примесей одновременно с коллекторными или базовыми областями транзисторов. Области, создаваемые вместе с эмиттера­ми транзисторов, применяются для этой цели реже, так как они имеют слишком малое удельное сопротивление.

При использовании в технологическом процессе производства ИМС ионной имплантации примесей резисторы могут создаваться как одновременно с изготовлением областей транзистора, так и независимо. Кроме того, возможно применение резисторов, полу­ченных путем вакуумного напыления на поверхность полупровод­никового кристалла тонких пленок металлов или сплавов (в этом случае микросхемы называются совмещенными). В последнее вре­мя получили развитие резисторы из поликристаллического крем­ния, нанесенного на поверхность кристалла.

Структуры резисторов, получаемых путем диффузии примесей, показаны на рисунке 1.1. Там же схематично показано распределение концентрации примесей в слоях полупровоадниковых структур, об­разующих резистор.

Если микросхема должна содержать резисторы с достаточно высоким сопротивлением (порядка нескольких десятков килоом и более), то изготовляются так называемые сжатые резисторы (пинч-резисторы). В варианте пинч-резистора, изображенного на рисунке 1.1, г, в качестве резистивного слоя используется базовый, а эмит-терный слой полностью перекрывает резистивную полоску и в полупроводниковой структуре непосредственно контактирует с кол­лекторным слоем. Соединенные таким образом коллекторный и эмиттерный слои могут играть роль полевых затворов, если на них подавать обратное по отношению к резистивному слою смещение. Аналогичную конструкцию имеет пинч-резистор, в котором резис-тивным слоем является коллекторная область транзистора (Рисунок 1.3 б).бОдним из основных параметров, характеризующих резистор, является сопротивление квадрата площади резистивного слоя ркв. Поясним смысл этого параметра, используя известную формулу для расчета электрического сопротивления R :

R = pl/(bd) (2.1)

где р — объемное удельное сопротивление, Ом-см; l — длина, см;

bud — размеры поперечного сечения (ширина и толщина) резистивного слоя, см.

Обозначим отношение p/d = p_KB , получив таким образом указанный параметр, измеряемый в Ом/кв. Формула примет вид,

R=p_кв l/b (2.2)

Использование параметра удельного сопротивления р_кв предполагает, что толщина d тонкого слоя или пленки фиксирована. Другими словами, сравнение удельных сопротивлений тонких слоев ] пленок может производиться по данному параметру исключительно при фиксированной (но не обязательно одинаковой) их толщин?

Введем понятие коэффициента формы резистора k _ф — 1/ b , с учетом которого формула преобразуется к виду

(2.3)

Другим важным параметром резистора является температурный коэффициент сопротивления (ТКС):

(2.4)

где Т — температура.

Если в интервале температур (T₂ —T₁ ) изменение сопротивле­ния ( R ₂ — R ₁ ) связано с изменением температуры линейной зави­симостью, то ТКС описывается формулой

(2.5)

Таблица 2.1

Nbg Тип резистора	Номинальные значения сопротивления, Ом	Погрешность, %	Удельное сопротивление, ркв , Ом/кв	ТКС, 1/град
Эмиттерный слой	2,5-103	+ 10	2-6	2*10-3
Базовый слой	150 – 20*103	+ 10	50-250	2*10-3
Коллекторный слой	250 – 10*103	+ 10	200-300	5*10-3
Сжатые резисторы	(5 – 500)*103	+ 20	(2-10)*103	5*10-3

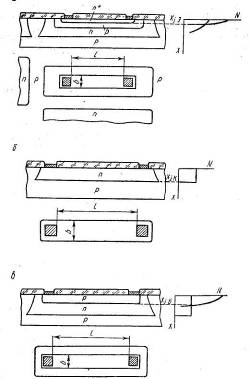
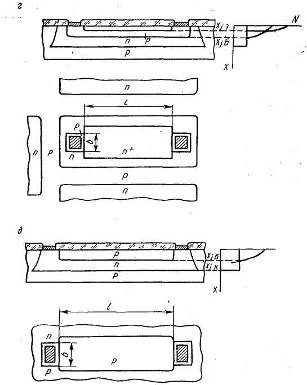
Рисунок 2.1 Структуры резисторов полупроводниковых микросхем: а —на основе эмиттерного слоя; 6 —на основе базового слоя; в —на основе коллекторного слоя; г—сжатый резистор на основе базового слоя; д— сжатый резистор на основе коллекторного слоя.

Полупроводниковые резисторы обладают паразитной распре­деленной емкостью, что является их недостатком. Паразитная ем­кость может быть охарактеризована коэффициентом

(2.6)

где С_кв — удельная паразитная распределенная емкость квадрата резистивной полоски, пФ/кв; ,р_кв — сопротивление квадрата резистивной полоски, кОм/кв; b — ширина резистора, мкм. :

Значения коэффициента Кн для некоторых вариантов резисто­ров приведены В таблице.

К недостаткам полупроводниковых резисторов относятся так­же сравнительно высокий ТКС и зависимость номинального сопро­тивления от величины приложенного к резистору напряжения, которое может модулировать площадь поперечного сечения резистивной полоски вследствие полевого эффекта. Кроме того, в резисто­рах, изолированных р- n-переходом, может проявляться паразит­ный транзисторный эффект. Максимально допустимое напряжение зависит от характеристики слоя, образующего резистор, и опреде­ляется пробивным напряжением р — л-перехода, отделяющего резистивный слой от остальных областей структуры.

Использование ионной имплантации примесей позволяет полу­чать тонкие резистивные слои с высоким удельным сопротивлени­ем р_кв , а также ТКС, слабо изменяющимся в достаточно широком интервале температур. Применяя дополнительную селективную обработку резистивного слоя лучом лазера, можно корректировать сопротивление резистора за счет изменения профиля распределе­ния примесей в данной части слоя.

Достоинствами резисторов, изготовленных нанесением на по­верхность кристалла ИМС металлических или поликристалличес­ких кремниевых пленок, являются независимость их сопротивления от величины напряжения, поданного на резистор, а также меньшие паразитные емкости и ТКС по сравнению с диффузионными или имплантированными резисторами. Металлические и поликремние­вые резисторы также поддаются корректировке путем пропускания через них электрического тока (плотность тока в импульсе не ме­нее 10⁶ А/см² ) или обработки лучом лазера. Изменение сопротив­ления при этом происходит вследствие изменений кристаллической: структуры пленок (размеров зерен, перераспределения примесей и т. п.).

Коэффициент паразитной емкости резисторов Таблица 2.2

Тип резисторов	Коэффициент К R (пФ/(кОм-мкм2 )) при удельном сопротивлении эпитаксиального коллекторного слоя р
р=1 Ом-см	р=6 Ом-см	р=10 Ом-см
Базовый слой Сжатые резисторы на основе: базового слоя коллекторного слоя	1*10-3 2,7*10-5 8*10-5	5*10—4 1,6*10-3 4*10-5	4,5*10-4 1,1*10-5 2,8*10-5

Расчет диффузионных и имплантированных резисторов заклю­чается в определении их геометрических размеров с учетом профи­ля распределения примесей в полупроводниковых слоях. Основны­ми условиями, принимаемыми во внимание при расчете, являются обеспечение необходимой мощности рассеяния резистора и задан­ной погрешности номинального сопротивления. С одной стороны, исходя из условия заданной мощности рассе­яния Р и допустимой удельной мощности Р_о , можно выразить пло­щадь, занимаемую резистивным слоем, как S = P / P ₀ . С другой стороны, площадь определяется геометрическими размерами S = = l / b . Поскольку длина резистивной полоски равна l = bk _ф , то пло­щадь может быть выражена соотношением S = b ² k _ф . Таким обра­зом, минимальная ширина резистивной полоски, найденная из ус­ловия рассеиваемой мощности, определяется выражением

(2.7)

Максимально допустимая удельная рассеиваемая мощность со­ставляет Ро=8 Вт/мм² для диффузионных и имплантированных ре­зисторов. Номинальная рассеиваемая мощность полупроводнико­вых резисторов обычно не превышает 10 мВт.

Требования, предъявляемые к допустимой погрешности номи­нального значения сопротивления резистора, также ограничивают номинальную ширину резистивной полоски. Если задана допусти­мая относительная погрешность сопротивления резистора уя — = AR / R , которая должна обеспечиваться в интервале рабочих темпе­ратур микросхемы в течение всего периода эксплуатации (в том числе без электрической нагрузки), то расчет резистора ведется с учетом ТКС и изменения сопротивления вследствие процессов вре­менного старения.

Относительное отклонение сопротивления вследствие измене­ния температуры определяется как

(2.8)

Относительное изменение сопротивления из-за процессов ста­рения -улт целесообразно учитывать только для поликремниевых и металлических резисторов, поскольку их пленочная поликристал­лическая структура более чувствительна к воздействию окружаю­щей среды, чем монокристаллические слои диффузионных или им­плантированных резисторов. Данные о величинах y_Rc ? являются эмпирическими справочными параметрами.

Кроме того, систематическое отклонение от номинального со­противления резистора вносится сопротивлениями контактов. Сопротивление контакта зависит от удельного сопротивления материа­ла резистивного слоя и условий растекания тока в приконтактной области: R_конт = р_кв k _раст , где коэффициент растекания k_раст = 0,14 для резистора с топологией, изображенной на рисунке 2.2, а, и К_{р аст} = 0,65 — на рисунке 2.2, б.

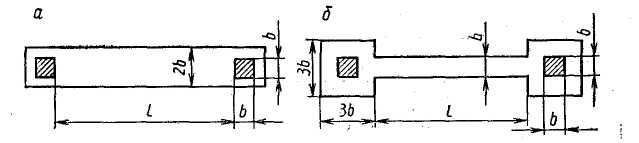
Рисунок 2.2. Топологические конфигурации полупроводниковых рези­сторов: а— низкоомный резистор; б— высокоомный резистор.

Относительное изменение сопротивления резистора вследствие наличия двух контактов составит

(2.9)

Принимая во внимание указанные систематические отклонения сопротивления резистора от заданного, найдем расчетное значение допустимой относительной погрешности:

(2.10)

Полученное значение _{R расч} может быть положено в основу дальнейшего расчета резистора с учетом случайных отклонений сопротивления, возникающих в процессе изготовления. Исходя из формулы выразим относительную технологическую погреш­ность (среднеквадратичное отклонение при. нормальном законе статистического распределения) следующим образом:

(2.11)

Где , , - относительные и абсолютные СКО соответствующих величин.

Полагая, что абсолютные среднеквадратичные отклонения гео­метрических размеров длины и ширины равны, т. е. l~b, и учитывая равенство l = bk _ф , преобразуем формулу к виду

(2.12)

Из последнего соотношения может быть определена минималь­ная ширина резистивной полоски:

(2.13)

Для типовых технологических процессов изготовления полу­проводниковых ИМС можно принимать АЬ = 0,5 мкм и yp_kb =005.

Полученные в результате расчета по формулам значения ширины резистивной полоски должны быть сопоставлены с минимальной шириной линии, обеспечиваемой принятой техноло­гией, т. е. с разрешающей способностью технологии, бтехн. Прини­мается максимальное из трех полученных значений

(2.14)

которое окончательно округляется в большую сторону.

Удельное сопротивление квадрата площади резистивиого слоя зависит от толщины слоя и структуры резистора. Резистивный слой может быть ограничен одним (Рисунок 2.1, а — в) или двумя р — n-переходами. Поскольку примесь в полученном диффузией резистивном слое распределена неравномерно, расчет удельного объемного сопротивления материала слоя трудо­емок.

Номограммы позволяют найти усредненную удельную объем­ную проводимость о резистивного слоя в зависимости от поверхно­стной концентрации акцепторных примесей Ns _а , концентрации донорных примесей в исходном материале (эпитаксиальном слое) N_{d 0} и отношения текущей координаты х р —n -перехода (если он имеется), ограничивающего резистивный слой сверху, к глубине р — n -перехода Xj , ограничивающего резистивный слой снизу. Например, для резистора, изображенного на рисунке 2.1, а, это отно­шение x|x_j = 0, поскольку резистивный слой начинается непосред­ственно на поверхности кристалла.

Таким образом, удельное сопротивление квадрата резистивного слоя

(2.15)

где d _рез = x_j — х — толщина резистивного слоя.

Типичные значения р_кв для резисторов на основе различных слоев полупроводниковой транзисторной структуры приведены В таблице.

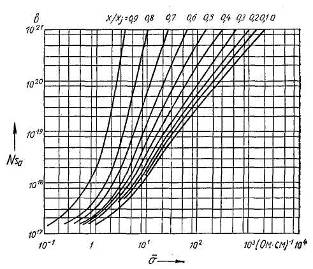
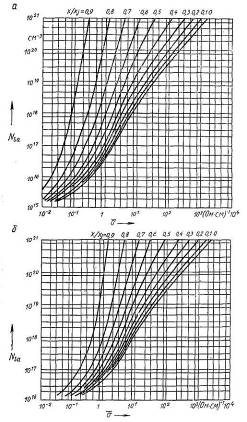
Рисунок 2.3. Номограммы для определения проводимости полупроводниковых областей, полученных диффузией акцепторной примеси, в материал с различной исходной концентрацией донорной примеси N_d :

а) N_do =10¹⁵ см^-3 ; б) N_do =10¹⁶ см^-3 в) N_do =10¹⁷ см^-3 (3.2.16)

Резисторы широко используются в аналоговых полупроводниковых ИМС, а также в аналоговых подсистемах БИС и СБИС В логических ИМС и ИМС для запоминающих устройств примене­ние резисторов постоянно сокращается. Это объясняется переходом к снижению рабочих токов и напряжений, что ведет к необходимо­сти увеличения размеров резисторов (длины, занимаемой площа­ди), т. е. к увеличению размеров ИМС. В микросхемах с инжекционным питанием, в частности, резисторы как элементы ИМС исключены почти полностью.

С помощью низкоомных резистивных слоев в полупроводнико­вых ИМС выполняются пересечения токопроводящих дорожек межсоединений (Рисунок 2.2). При этом металлическая или поликремние­вая дорожка проходит поверх окисла, в то время как низкоомная резистивная дорожка — под окислом.

ЛИТЕРАТУРА

1. Черняев В.Н. Технология производства интегральных микросхем и микропроцессоров. Учебник для ВУЗов - М; Радио и связь, 2007 - 464 с: ил.

2. Технология СБИС. В 2 кн. Пер. с англ./Под ред. С.Зи,- М.: Мир, 2006.-786 с.

3. Готра З.Ю. Технология микроэлектронных устройств. Справочник. - М.: Радио и связь, 2001.-528 с.

4. Достанко А.П., Баранов В.В., Шаталов В.В. Пленочные токопроводящие системы СБИС.-Мн.: Выш.шк., 2003.-238 с.

5. Таруи Я. Основы технологии СБИС Пер. с англ. - М.: Радио и связь, 2005-480 с.

Скачать архив с текстом документа