Розвязок задачі лінійного програмування

СОДЕРЖАНИЕ: Послідовність графічного розвязання задачі лінійного програмування. Сумісна система лінійних нерівностей, умови невідємності, визначення півплощини з граничними прямими. Графічний метод для визначення оптимального плану задачі лінійного програмування.

Задача 1

Розв’язати графічно задачу лінійного програмування

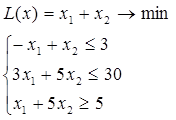
Розв’язання:

Розглянемо на площині х1Оx2 сумісну систему лінійних нерівностей

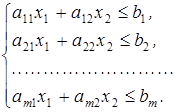(1)

Кожна нерівність цієї системи геометрично визначає півплощину з граничною прямою (i = 1, 2,...,т). Умови невід’ємності визначають півплощини відповідно з граничними прямими . Система сумісна, тому півплощини, як опуклі множини, перетинаючись, утворюють спільну частину, що є опуклою множиною і являє собою сукупність точок, координати кожній із який є розв’язком даної системи (рис. 1.).


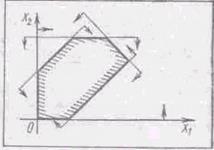
Рис. 1.

Сукупність цих точок (розв’язків) називають багатокутником розв’язків Він може бути точкою, відрізком, променем, багатокутником, необмеженою багатокутною областю.

Якщо в системі обмежень (1) п = 3, то кожна нерівність геометрично представляє півпростір тривимірного простору, гранична площина котрого (i = 1, 2,...,т), а умови невід’ємності – півпростори з граничними площинами відповідно хі = 0 (і = 1,2,3). Якщо система обмежень сумісна, то ці півпростори, як опуклі множини, перетинаючись, утворять у тривимірному просторі спільну частину, що називається багатогранником розв’язків. Багатогранник розв’язків може бути точкою, відрізком, променем, багатокутником, багатогранником, багатогранною необмеженою областю.

Нехай у системі обмежень (1) п 3; тоді кожна нерівність визначає півпростір n-вимірного простору з граничною гіперплощиною (i = 1, 2,...,т),. Кожному обмеженню виду (3.7) відповідають гіперплощина та напівпростір, який лежить по один бік цієї гіперплощини, а умови невід’ємності – півпростори з граничними гіперплощинами хі = 0 (і = 1,2,3,...,n).

Якщо система обмежень сумісна, то по аналогії з тривимірним простором вона утворює спільну частину в n-вимірному просторі – опуклий багатогранник допустимих розв’язків.

Таким чином, геометрично задача лінійного програмування являє собою відшукання такої точки багатогранника розв’язків, координати, якої надають лінійній функції максимальне (мінімальне) значення, причому допустимими розв’язками є усі точки багатогранника розв’язків.

Цільову функцію в п-вимірному просторі основних змінних можна геометрично інтерпретувати як сім’ю паралельних гіперплощин, положення кожної з яких визначається значенням параметра Z.

Запишемо систему нерівностей у вигляді:

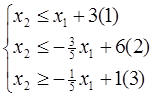
Розв’яжемо задачу графічно.

Побудуємо систему обмежень (1), (2), (3).

Побудуємо також лінії рівня: х1 + х2 = С. С = const.

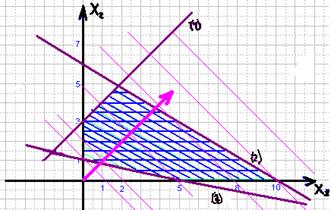
Розв’язок на перетині Ох2 та (3):

Отже, розв’язок є точка , причому .


Задача 2

Розв’язати симплекс методом:

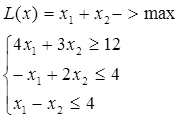
Розв’язання:

Графічний метод для визначення оптимального плану задачі лінійного програмування доцільно застосовувати лише для задач із двома змінними. За більшої кількості необхідно застосовувати загальний метод розв’язування задач лінійного програмування. З властивостей розв’язків задачі лінійного програмування відомо: оптимальний розв’язок задачі має знаходитись в одній з кутових точок багатогранника допустимих розв’язків. Тому найпростіший спосіб відшукання оптимального плану потребує перебору всіх кутових точок (можливих допустимих планів задачі). Кожний опорний план визначається системою m лінійно незалежних векторів, які містяться в системі обмежень задачі з n векторів , отже загальна кількість опорних планів визначається кількістю комбінацій

.

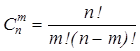Задачі, що описують реальні економічні процеси мають значну розмірність і простий перебір всіх можливих опорних планів таких задач є дуже складним, навіть за умови застосування сучасних ЕОМ. Отже необхідне використання методу, який дає можливість скоротити кількість обчислень. Такий метод запропоновано американським вченим Дж. Данцігом у 1949 році – так званий симплекс-метод.

Ідея методу полягає в здійсненні направленого перебору допустимих планів, таким чином, що на кожному кроці здійснюється перехід від одного опорного плану до наступного, який є хоча б не гіршим за попередній. Значення функціоналу при переході змінюється в потрібному напрямку: збільшується (для задачі на максимум) чи зменшується (для задачі на мінімум).

Процес розв’язування задачі симплекс-методом має ітераційний характер: однотипові обчислювальні процедури (ітерації) повторюються у певній послідовності доти, доки не буде отримано оптимальний план задачі або з’ясовано, що його не існує.

Отже, симплекс-метод — це поетапна обчислювальна процедура, яка дозволяє починаючи з відомого опорного плану за скінчену кількість кроків отримати оптимальний план задачі лінійного програмування.

Розглянемо задачу лінійного програмування подану в канонічній формі:

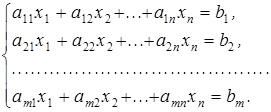
Не втрачаючи загальності припустимо, що система містить перші m одиничних векторів:


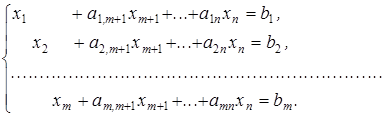(1)

(2)

(3)

Система (1) у векторній формі матиме вигляд:

(4)

де

, ,..., ,

, ,..., ,

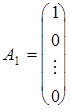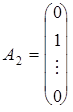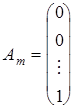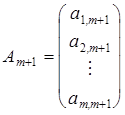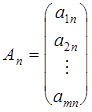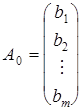– лінійно незалежні одиничні вектори m-вимірного простору, що утворюють одиничну матрицю і складають базис цього простору. Тому в розкладі (4) базисними змінними будуть , інші – вільні змінні. Покладемо всі вільні змінні рівними нулю . Оскільки , а вектори – одиничні, отримаємо один із розв’язків системи (4), тобто допустимий план.

(5)

Такому плану відповідає розклад

(6)

де – лінійно незалежні і за властивістю 3 розв’язків задачі лінійного програмування план є кутовою точкою багатогранника розв’язків, а отже може бути початковим опорним планом.

Розглянемо, як виходячи з початкового опорного плану (5) перейти до наступного опорного плану, що відповідає процесу перебору кутових точок багатогранника розв’язків.

Оскільки є базисом m-вимірного простору, то кожен з векторів співвідношення (5) може бути розкладений за векторами базису причому єдиним чином:

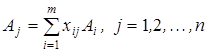
Розглянемо такий розклад для довільного не базисного вектора, наприклад, для :

(7)


Припустимо, що у виразі (7) існує хоча б один додатній коефіцієнт .

Введемо до розгляду деяку поки що невідому величину , помножимо на неї обидві частини рівності (3.34) і віднімемо результат з рівності (3.33), маємо:

(8)

Таким чином вектор

є планом у тому випадку, коли його компоненти невід’ємні. За припущенням , отже ті компоненти вектора в які входять будуть невід’ємними, тому необхідно розглядати лише ті компоненти, які містять додатні . Отже необхідно знайти таке значення , при якому для всіх буде виконуватися умова невід’ємності плану задачі:

(9)

З (3.36) отримуємо, що для шуканого має виконуватися умова 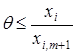. Отже вектор буде планом задачі для будь-якого q, що задовольняє умову


,

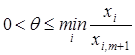де мінімум знаходимо по тих i, для яких .

Опорний план не може містити більш ніж m додатних компонент, тому в плані необхідно перетворити в нуль хоча б одну з компонент. Припустимо, що

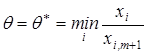
для деякого значення і, тоді відповідна компонента плану перетвориться в нуль. Нехай це буде перша компонента плану, тобто

.

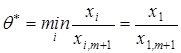Підставимо значення у вираз:

,

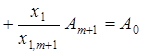якщо позначити

, ,


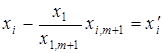
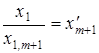то рівняння можна подати у вигляді розкладу:

,

якому відповідає наступний опорний план:

.

Для визначення наступного плану необхідно аналогічно продовжити процес: будь-який вектор, що не входить в базис розкласти за базисними векторами, а потім визначити таке , для якого один з векторів виключається з базису.

Узагальнюючи розглянутий процес, маємо – визначення нових опорних планів полягає у виборі вектора, який має ввійти в базис і вектора, що має вийти з базису. Така процедура відповідає переходу від одного базису до іншого за допомогою методу Жордана-Гауса.

Необхідно відмітити, що для випадку коли вектор підлягає включенню в базис, а в його розкладі всі , то, очевидно, не існує такого , який виключав би один з векторів розкладу (3.35). В такому випадку план містить m+1 додатних компонент, отже система векторів буде лінійно залежною і визначає не кутову точку багатогранника розв’язків, а функціонал не може в ній досягати свого максимального значення. Це означає, що функціонал є необмеженим на багатограннику розв’язків.

Симплексний метод здійснює направлений перебір опорних планів, що дозволяє переходити від одного плану до іншого, який є хоча б не гіршим від попереднього за значенням, що він надає функціоналу. Отже окремим питанням постає вибір вектору, який необхідно вводити в базис при здійсненні ітераційної процедури симплексного методу.

Теорема 1. Якщо для деякого вектора виконується умова , то план не є оптимальним і можливо побудувати такий план Х, для якого виконуватиметься нерівність .

Доведення. Помножимо (3.39) і (3.40) на і віднімемо результати відповідно з (3.37) та (3.38), отримаємо:

(*)

У співвідношенні до обох частин додається величина для , додатні, тому завжди можливо знайти таке , що всі коефіцієнти при векторах були невід’ємними, іншими словами отримати новий план задачі виду:

,

якому згідно відповідає значення функціоналу

Так як за умовою теореми

і , то .


Що і потрібно було довести.

Теорема 2. Якщо для деякого вектора виконується умова , то план не є оптимальним і можливо побудувати такий план Х, для якого виконуватиметься нерівність .

Запишемо канонічну задачу:

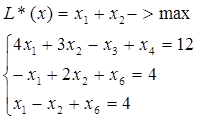
Розв’яжемо симплекс-методом:

1 1 0 -M 0 0
x1 x2 x3 x4 x5 x6 B T
x4 4 3 -1 1 0 0 12 3 **
x5 -1 2 0 0 1 0 4 –
x6 1 -1 0 0 0 1 4 4
F -1 -1 0 0 0 0 0 0
Mf -4 -3 1 0 0 0 -12 0
**
1 1 0 -M 0 0
x1 x2 x3 x4 x5 x6 B T
x1 1 0,75 -0,25 0,25 0 0 3 4
x5 0 2,75 -0,25 0,25 1 0 7 2,545 **
x6 0 -1,75 0,25 -0,25 0 1 1 –
F 0 -0,25 -0,25 0,25 0 0 3 0
Mf 0 0 0 1 0 0 0 0
**
1 1 0 -M 0 0
x1 x2 x3 x4 x5 x6 B T
x1 1 0 -0,1818 0,1818 -0,2727 0 1,091 –
x2 0 1 -0,09091 0,09091 0,3636 0 2,545 –
x6 0 0 0,09091 -0,09091 0,6364 1 5,455 60 **
F 0 0 -0,2727 0,2727 0,09091 0 3,636 0
Mf 0 0 0 1 0 0 0 0
**
1 1 0 -M 0 0
x1 x2 x3 x4 x5 x6 B T
x1 1 0 0 0 1 2 12 –
x2 0 1 0 0 1 1 8 –
x3 0 0 1 -1 7 11 60 60
F 0 0 0 0 2 3 20 0
Mf 0 0 0 1 0 0 0 0

Отже, х* = (12, 8, 60), L(x*)max = 20.

Задача 3

Для задачі побудувати двоїсту, розв’язати і за розв’язком знайти розв’язок двоїстої:

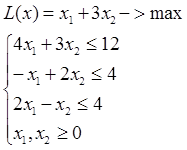
Розв’язання:

Кожна задача лінійного програмування пов’язана з іншою, так званою двоїстою задачею.

Економічну інтерпретацію кожної з пари задач розглянемо на прикладі виробничої задачі.

Початкова задача:


max z = c1x1 + c2x2 + … + cnxn

,

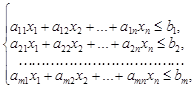
Визначити, яку кількість продукції кожного j-го виду необхідно виготовляти в процесі виробництва, щоб максимізувати загальну виручку від реалізації продукції підприємства. Причому відомі: загальна кількість ресурсів – , нормативи використання кожного і-го виду ресурсу на кожен j-ий вид продукції – , а також – ціна реалізації одиниці продукції.

Розглянемо тепер ту саму задачу з іншої точки зору. Припустимо, що за певних умов доцільно продавати деяку частину чи всі наявні в господарстві ресурси. Необхідно визначити цінність ресурсів. Кожному ресурсу поставимо у відповідність його оцінку . Умовно вважатимемо, що – ціна одиниці і-го ресурсу.

На виготовлення одиниці j-го виду продукції витрачається згідно моделі всі m видів ресурсів у кількості відповідно . Оскільки ціни одиниці кожного виду ресурсів за припущенням дорівнюють , то загальна вартість ресурсів, що витрачені на виробництво одиниці j-го виду продукції обчислюється як


Продавати ресурси доцільно лише за умови, що кошти отримані в результаті продажу ресурсів будуть дорівнювати або перевищуватимуть суму, яку можливо було б отримати за реалізацію продукції виготовленої з тієї самої кількості ресурсів, тобто

.

Зрозуміло, що покупці ресурсів прагнуть здійснити операцію якнайдешевше, отже необхідно визначити мінімальну вартість одиниці кожного виду ресурсів за якої їх продаж є більш доцільним ніж виготовлення продукції. Загальна вартість ресурсів виражається величиною

.

Отже в результаті маємо двоїсту задачу:

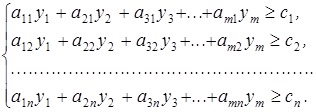
Визначити, які мінімальні ціни можливо встановити для одиниці кожного і-го виду ресурсу , щоб продаж ресурсів був більш доцільним ніж виробництво продукції. Причому відомі: загальна кількість ресурсів – , нормативи використання кожного і-го виду ресурсу на кожен j-ий вид продукції – , а також – ціна реалізації одиниці продукції.

Для побудови двоїстої задачі необхідно звести початкову до стандартного виду. Задача лінійного програмування подана у стандартному вигляді, якщо для відшукання максимального значення цільової функції всі нерівності системи обмежень приведені до вигляду «», а для задачі відшукання мінімального значення – до вигляду «».

Якщо пряма задача лінійного програмування подана в стандартному вигляді, то двоїста задача утворюється за такими правилами:

1. Кожному обмеженню прямої задачі відповідає змінна двоїстої задачі. Кількість невідомих двоїстої задачі дорівнює кількості обмежень прямої задачі.

2. Кожній змінній прямої задачі відповідає обмеження двоїстої задачі, причому кількість обмежень дорівнює кількості невідомих прямої задачі.

3. Якщо цільова функція прямої задачі задається на пошук найбільшого значення (max), то цільова функція двоїстої задачі — на визначення найменшого значення (min), і навпаки.

4. Коефіцієнтами при змінних в цільовій функції двоїстої задачі є вільні члени системи обмежень прямої задачі.

5. Правими частинами системи обмежень двоїстої задачі є коефіцієнти при змінних в цільовій функції прямої задачі.

6. Матриця

,


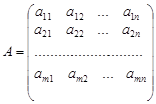що складається з коефіцієнтів при змінних у системі обмежень прямої задачі, і матриця коефіцієнтів в системі обмежень двоїстої задачі

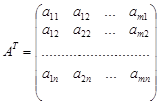
утворюються одна з одної транспонуванням, тобто заміною рядків стовпчиками, а стовпчиків — рядками.

Теорема (перша теорема двоїстості). Якщо одна з пари спряжених задач має оптимальний план, то і інша також має розв’язок, причому для оптимальних розв’язків значення цільових функцій співпадають .

Якщо цільова функція однієї із задач не обмежена, то інша задача також не має розв’язку.

Між розв’язками спряжених задач крім рівності значень цільових функцій, існує більш тісний взаємозв’язок. Для його дослідження розглянемо дві симетричні задачі лінійного програмування.

Пряма задача: Двоїста задача:


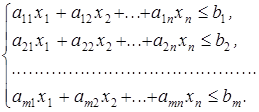
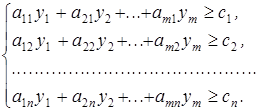
Для розв’язування задач симплексним методом необхідно привести їх до канонічної форми, для чого в систему обмежень задачі необхідно ввести m невід’ємних змінних, а в систему обмежень – n невід’ємних змінних. Поставимо обмеженням кожної задачі у відповідність змінні двоїстої.

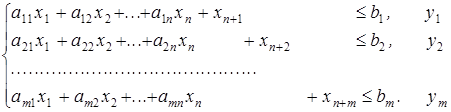
Аналогічно:

Отримали наступну відповідність між змінними спряжених задач:

Основні змінні прямої задачі Додаткові змінні прямої задачі



Додаткові змінні двоїстої задачі Основні змінні двоїстої задачі

Наступна теорема в літературі як правило має назву теореми про доповнюючу нежорсткість.

Теорема (друга теорема двоїстості для симетричних задач). Для того, щоб плани та відповідних спряжених задач були оптимальними, необхідно і достатньо щоб виконувалися умови доповнюючої нежорсткості:

.

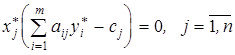
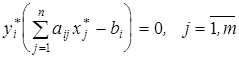Більш очевидно взаємозв’язок між оптимальними планами прямої та двоїстої задач встановлює наслідок другої теореми двоїстості.

Наслідок. Якщо в результаті підстановки оптимального плану однієї із задач (прямої чи двоїстої) в систему обмежень цієї задачі і-те обмеження виконується як строга нерівність, то відповідний і-ий компонент оптимального плану спряженої задачі дорівнює нулю.

Якщо і-ий компонент оптимального плану однієї із задач додатний, то відповідне і-те обмеження спряженої задачі виконується для оптимального плану як рівняння.

Побудуємо двоїсту:

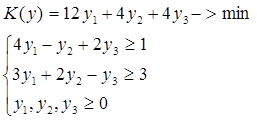
Побудуємо симплекс таблиці для прямої задачі:

1 3 0 0 0
x1 x2 x3 x4 x5 B T
x3 4 3 1 0 0 12 4
x4 -1 2 0 1 0 4 2 **
x5 2 -1 0 0 1 4 ###
F -1 -3 0 0 0 0 0
**
1 3 0 0 0
x1 x2 x3 x4 x5 B T
x3 5,5 0 1 -1,5 0 6 1,09 **
x2 -0,5 1 0 0,5 0 2 ###
x5 1,5 0 0 0,5 1 6 4
F -2,5 0 0 1,5 0 6 0
**
1 3 0 0 0
x1 x2 x3 x4 x5 B T
x1 1 0 0,18 -0,27 0 1,09 1,09
x2 0 1 0,09 0,36 0 2,55 ###
x5 0 0 -0,27 0,91 1 4,36 4
F 0 0 0,45 0,82 0 8,73 0

Отже, максимум F дорівнює 8,73 в точці (1,09, 2,55).

Тоді мінімум К(у) дорівнює також 8,73. у* = (0, 2,33, 1,67)Т.

Задача 4

Методом потенціалів розв’язати ТЗ.

Розв’язання:

Q1 Q2 Q3 Q4 Q5 a
P1 7 3 1 5 4 30
P2 7 5 8 3 2 25
P3 6 4 8 3 2 45
P4 3 1 7 6 2 20
b 10 35 15 25 35

10 +35+15+25+35 = 120

30+ 25+ 45+ 20 = 120.

Отже, ТЗ є закритою.

Знайдемо початковий план методом пн-зх кута.

Q1 Q2 Q3 Q4 Q5 a
P1 7 3 1 5 4 5
10 20
P2 7 5 8 2 2 25
15 10
P3 6 4 8 2 2 10
5 25 15
P4 3 1 7 2 2 20
20
b 10 10 15 25 10

Поетапно проведемо методом потенціалів розв’язок задачі:

Q1 Q2 Q3 Q4 Q5 u
P1 7 3 - 1 + 5 4 4
10 20 -5 5 4
P2 7 5 + 8 - 2 2 6
-2 15 10 0 0
P3 6 4 8 2 2 6
-3 -1 5 25 15
P4 3 1 7 2 2
0 2 5 6 20
v 3 -1 2 -4 -4
Q1 Q2 Q3 Q4 Q5 u
P1 7 - 3 1 + 5 4 4
10 10 10 10 9
P2 7 5 8 2 2 6
-2 25 5 5 5
P3 6 4 8 - 2 2 + 11
-8 -6 5 25 15
P4 3 + 1 7 2 2 - 11
-11 -9 -1 0 20
v 3 -1 -3 -9 -9
Q1 Q2 Q3 Q4 Q5 u
P1 7 3 1 5 4 5
5 10 15 7 7
P2 7 5 8 2 2 7
2 25 7 7 7
P3 6 4 8 2 2 1
7 7 7 25 20
P4 3 1 7 2 2 1
5 7 7 7 15
v 2 -2 -4 1 1

Всі оцінки Сij – vi – uj на 3 етапі невід’ємні, тому оптимальний розв’язок знайдено.

5 10 15 0 0
X = 0 25 0 0 0
0 0 0 25 20
5 0 0 0 15

Вартість перевезень дорівнює: 7 * 5 + 3 * 10 + 1 * 15 + 5 * 25 + 3 * 5 + 2 * 25 + 2 * 20 + 2 * 15 = 340.


Список використаних джерел

1. Бурий В.В., Шевченко І.В. Математичне програмування. — К.: НАУ, 2007. — 168с.

2. Єгоршин О.О., Малярець Л.М. Математичне програмування. — Х.: ВД ІНЖЕК, 2006. — 383с.

3. Жильцов О.Б., Кулян В.Р., Юнькова О.О. Математичне програмування (з елементами інформаційних технологій) / Міжрегіональна академія управління персоналом / Олена Олександрівна Юнькова (ред.). — К.: МАУП, 2006. — 184с.

4. Зеленський К.Х. Математичне програмування. — К.: Університет Україна, 2007. — 241c.

5. Лебідь М.Т., Синявіна ЮВ. Математичне програмування. — Х., 2007. — 72с.

Скачать архив с текстом документа