Застосування клина та важеля в техніці
СОДЕРЖАНИЕ: Золоте правило механіки, плоскість похилої, важіль і їх використання в машинах. Застосування клина для зєднання окремих деталей і частин механізму в єдине ціле. Коефіцієнт корисної дії. Опір жорсткості канатів і ланцюгів в передачах з гнучкими ланками.План
1.Плоскість похилої, важіль, клин і їх вживання в машинах
2. Рівновага сил на похилій плоскості
3. Золоте правило механіка
4. Важіль, його рівноваги і різновиди
5. Клин і застосування клина в техніці
6. К. К. Д. ворота, блока і поліспасту
Список використаної літератури
1 . Плоскість похилої, важіль, клин і їх вживання в машинах
На кордоні піщаної пустелі в Єгипті височіє ступінчаста піраміда Хеопса заввишки 146 м. Вона побудована з плит вагою по 2,5 т кожна. Очевидно, що люди, що зводили подібні споруди, не могли піднімати на висоту такі плити і глиби без елементарних механічних пристосувань, так званих простих механізмів.Одним з цих механізмів є плоскість похилої. Плоскість похилої дозволяє, користуючись малою силою, підняти або опустити великий вантаж. Тому принципи роботи похилої плоскості використовуються в багатьох конструкціях сучасних машин і механізмів, наприклад ланцюгові, стрічкові і канатні транспортери; гвинтове різьблення.
2. Рівновага сил на похилій плоскості
Розглянемо, які сили діють на тіло, поміщене на похилу плоскість АВ, підняту на висоту ВС (мал. 1). Позначимо: 
G
— вага тіла; P
— тягове зусилля; a
— кут нахилу плоскості до горизонту; в — кут, утворений тяговим зусиллям з похилою плоскістю; ѓ — коефіцієнт тертя; l
— довжина похилої плоскості АВ; h
— висота похилої плоскості ВС.
Власна вага тіла G , направлений вертикально вниз, розкладемо на дві складові: G 1 , паралельну похилій плоскості АВ , і G 2 , перпендикулярну до неї. Силу G 1 знаходимо з подібності трикутників АБС і OG 1 G :
тобто при користуванні похилою плоскістю ми отримуємо виграш в силі в стільки раз, в скільки разів довжина похилої плоскості більше її висоти. Але відношення
Розглянемо випадок, коли тіло рухається вгору по похилій плоскості. Щоб рівномірно піднімати тіло вгору по похилій плоскості з врахуванням тертя, необхідно прикласти до нього силу, великуG 1 на величину сили тертя, тобто має бути дотримане умова
Де F
–
сила тертя, викликана нормальним тиском N
оскільки 
то:
.
отже:
Підставляючи в це рівняння значення сил, отримуємо
.і 
Звідси: 
При русі тіла вниз по похилій плоскості напрям сили тертя буде протилежним вказаному на мал. 1, а отже, знак у формулі перед f має бути змінений на зворотний
4 . Золоте правило механіка
Якщо не враховувати силу тертя і опір середовища, то при підйомі тіла вагою G на висоту h здійснюється робота
при підйомі ж тіла по похилій плоскості здійснюється роботатобто користування похилою п плоскість не дає виграшу в роботі, оскільки в скільки разів ми виграємо в силі, в стільки ж раз програємо у відстані. Це правило справедливо для всіх машин. Воно отримало назву золотого правила механіки.
5. Важіль, його рівноваги і різновиди
Важіль , так само як і плоскість похилої, є простим механізмом, користуючись яким людина з малою силою може зробити велику роботу. Кліщі для витягування цвяхів, тачка, залізничний шлагбаум, підіймальний кран — все це приклади важеля.
У загальному вигляді важіль можна представити як стрижень, що має вісь обертання або точку опори, довкола якої він може обертатися під дією сил.
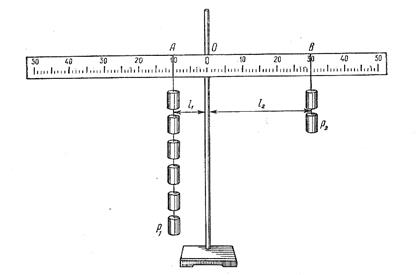
Рівновага вантажів, підвішених по кінцях стрижня, залежить як від їх ваги, так і від відстані до крапки опори стрижня. Очевидно, що два рівні вантажіпідвішених на різних відстанях від точки опори, врівноважують одне одного. У тих же умовах більший вантаж переважить менший. Якщо відсовувати менший вантаж вправо (мал. 2), то можна добитися того, що менший вантаж переважить більший.
За яких умов ми добємося виграшу з силі? Позначимо точку опори важеля буквою О , а крапки додатку сил — буквами .А і В. Прямі АР1 і ВР2 — лінії, уздовж яких діють сили Р1 і Р2 .
Перпендикуляр, опущений з точки опори важеля на лінію, вздовж якої діє сила, називається плечем сили, або плече сили є найкоротший шлях від точки опори до лінії дії сили . Відстань l 1 іl 2 – плечі сил Р1 і Р2 . Робота сили на плече дає момент сили:
M 1 = P 2 l 2 ; M 2 P 2 l 2
(мал. 1)
Важіль буде находитись в рівновазі , коли M 1 = M 2 момент сили ,обертаючи важіль за часовою стрілкою дорівнює моменту сили, обертів важеля проти стрілки P 1 l 1 = P 2 l 2 .
Користуючись важелем, ми виграємо в силі в стільки раз, в скільки одне плече більше іншого. Ми розглянули важіль, в якого точки додатка сил розташовані: по різні сторони від точки опори. Важелі такого типа прийнято називати важелями першого роду (залізничний шлагбаум). Часто використовуються важелі у яких точки прилягання сил лужать на одну сторону точки опори. Такі важелі називаються важелями другого роду
6. Клин і застосування клина в техніці
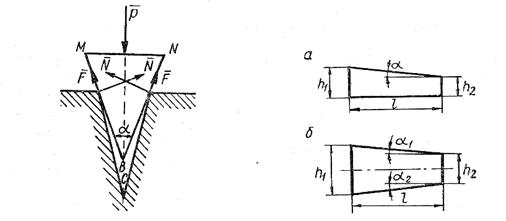
Клином є різновид похилої плоскості і має найрізноманітніше вживання. Він: наприклад, складає основну частину інструментів, що колють, ріжучих, стругаючих: сокири, колуна, стамески, ножиць, токарних і стругальних різців. Наприклад, при коління деревини (мал. 3) отримуємо виграш в силі в стільки раз, в скільки довжина щоки МБ ,більше обуха сокири MN.
В техніці клином називають стержень, застосовується для з’єднання окремих деталей і частин механізму в єдине ціле.
(мал. 2 а)и (мал. 2 б)
Він встановлюється в спеціальний отвір – і утримує в ньому силами тертя. Найбільш характерними сферами застосування клину є зєднання тяги, поршневих штоків з крейцкопфами (повзунами) парових машин і насосів, половинок маховиків, валу і маточини (клиновими шпонками), пристосуванні для обробки деталей на верстатах.
Залежно від напряму дії сил на клин клинові зєднання бувають подовжні і поперечні. До поперечних відносяться клини, до подовжніх — шпонки.Клин може мати ухил з однією (мал. 3, а) або з двох (мал. 3, б) сторін.
Для однобічного клину нахил:
Для двохстороннього клина нахилу:
Поперечний клин з паралельними сторонами і виступами, перешкоджаючи його випаданню, називають чекою. Основна умова, якій повинно задовольняти клинове зєднання, полягає в тому, щоб при навантаженні деталей, що скріпляються, клин не видавлювався з гнізда.
7 . К. К. Д. ворота, блока і поліспасту
важіль клин застосування
Енергія, споживана машиною, витрачається на подолання корисних і шкідливих опорів. До перших відносять так звані сили виробничих опорів, для подолання яких побудована та або інша машина, наприклад опір матеріалу зміні форми в робочих машинах, вага вантажу у вантажопідйомних пристроях.
До других відносяться сили шкідливих опорів, що виникають в самій машині в процесі її роботи. Це сили тертя в кінематичних парах, опір жорсткості канатів і ланцюгів в передачах з гнучкими ланками, опір змащувального шару і ін. Робота рушійних сил за повний цикл при сталому русі витрачається на подолання виробничих і шкідливих опорів.
Машина є тим більше здійсненою, ніж більша частина споживаної нею енергії витрачається на подолання корисних опорів. Міра досконалості машини характеризується відношенням, що виражає коефіцієнт корисної дії.
Коефіцієнтом корисної дії (К. К. Д.) машини називають відношення роботи сил корисних опорів до роботи сил рушійних.
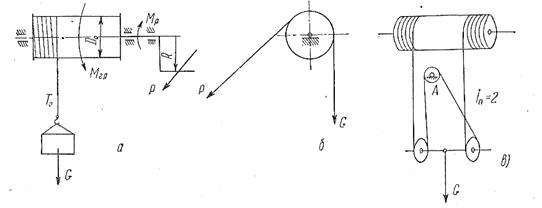
Коефіцієнтом корисної дії можна оцінювати міру досконалості не лише машини, але і будь-якого, простого, такого, що не є машиною пристосування, що сприймає і віддає енергію. Розглянемо К. К. Д. коміра (мал. 79, а), блоку (мал.4) і поліспасту (мал. 4, в).
Всі ці механізми використовуються для підйому вантажу за допомогою канатів або ланцюгів, причому блоки застосовуються в підіймальному механізмі для зміни напряму гнучкого органу, або є ланками поліспасту. Поліспаст вводиться в підіймальний механізм для зменшення натягнення
(мал.2)
гнучкого органу і вантажного моменту на барабані. Економічною метою введення поліспасту є зменшення передавального відношення передавального механізму, а отже, його розмірів, ваги і вартості. Комір складається з циліндрового барабана, на який навивається канат (або ланцюг) з підвішеним до нього вантажем, і валу з рукояткою. Натягнення каната То , рівне в даному випадку вазі вантажу G , створює на валу барабана вантажний момент
При підйомі або опусканні вантажу вантажний момент Мгр повинен врівноважуватися моментом Мр :
Або
Звідси
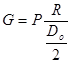
(Рівність (5) справедлива, якщо не враховувати втрат на тертя в підшипниках і витрат на подолання жорсткості каната.)
Оскільки зусилля людини навіть при короткочасній роботі рекомендується приймати не більш Pmax =30 кГ , збільшується радіусу рукоятки R обмежується довжиною рук люди ни, а зменшення діаметру барабана жорсткістю каната, то за допомогою такого коміра можна підняти не дуже великий вантаж. Коефіцієнт корисної дії ворота.
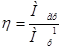
де
— момент для подолання Мгр
, жорсткості каната і тертя на осі барабана.
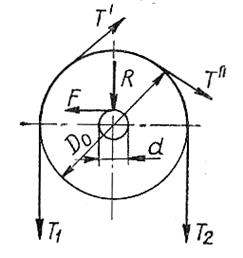
Розглянемо блок на мал. 5. При абсолютно гнучкому канаті і відсутності тертя на осі блоку натягнення Т1
і Т2
в набігаючій і збігаючій гілках каната мають бути рівні. Насправді ж для подолання жорсткості каната, тобто для його згинання і розгинання, потрібне деяке зусилля Т
, величина якого залежить від діаметру каната, діаметру Do
блоку , що огинається, натягнення каната Т
і його структури.Для практичних розрахунків можна приймати: для прядивних канатів Т
(0,04 
0,07) Т1
для дротяних канатів 
(0,010,02)Т1
, причому великі значення беруть для товстих канатів
мал. 5
Крім того, при обертанні блоку доводиться долати тертя на його осі. Тиск R блоку на вісь, якщо нехтувати власною вагою його, рівне Т1 + Т2 .
Сила тертя на осі F = Rf
, де f
— коефіцієнт тертя на осі. Для опор ковзання f
зазвичай приймають 0,08 0,1, а для підшипників кочення — 0,01 0,02.
Момент сили тертя :
Зусилля, необхідне для подолання цього моменту, віднесене до осі каната:
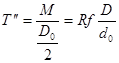
Внаслідок наявності опорів Т і Т натягнення в тій, що збігає з блоку гілки каната завжди більше натягнення набігаючої його гілки:
Т2
Т1
або Т2
= Т1
+ Т + Т
К.К. Д. всієї поліспастній системи визначається відношенням ідеальної величини натягнення до дійсної
В загальному виді
де ia— кратність поліспасту. Кратність поліспасту іп представляє відношення числа гілок, на яких підвішений вантаж, до гілок, що йдуть на барабан.
Рекомендована література
Рунець М.А. Технічна механіка, Мінск: Вища школа, 1970р.
Ердеді А.А. Технічна механіка: Теоретична механіка. Опір матеріалів: Підр.-М.: Вища школа, 1991р.
Аркуша А.І. Посібник для рішення задач по теоретичній механіці: М.: Вища школа,1971р.
Цасюк В. В. Теоретична механіка: Навчальний посібник. – Київ: Центр навчальної літератури, 2004. – 402с.