Сетевое планирование и управление в менеджменте 3
СОДЕРЖАНИЕ: РОССИЙСКАЯ МЕЖДУНАРОДНАЯ АКАДЕМИЯ ТУРИЗМА ФАКУЛЬТЕТ: Менеджмента и экономики туристского бизнеса КАФЕДРА: Управление персоналом в туризме Курсовая работаРОССИЙСКАЯ МЕЖДУНАРОДНАЯ АКАДЕМИЯ ТУРИЗМА
ФАКУЛЬТЕТ: Менеджмента и экономики туристского бизнеса
КАФЕДРА: Управление персоналом в туризме
Курсовая работа
По дисциплине: менеджмент
Тема: «Сетевое планирование и управление в менеджменте».
Вариант № 5
Выполнил:
Проверил:
Химки 2010
Содержание :
1 Теория сетевого планирования в менеджменте. 5
1.1.Сущность сетевого планирования и управления. 5
1.2.Элементы сетевой модели и их характеристики, правила построения6
1.3. Оптимизация и критерии оптимизации. 13
1.4. Область использования сетевой модели. 18
2 Построение и оптимизация сетевой модели. 20
2.1.Исходные данные для построения сетевой модели. 20
2.2. Графическое изображение сетевой модели. 21
2.3.Анализ сетевой модели и определение критического пути. 21
2.4. Расчеты собственных системных характеристик элементов. 23
2.5.Алгоритм оптимизации сетевой модели. 25
2.6. Результат оптимизации. 26
2.7. Сетевая модель после оптимизации. 28
Заключение. 29
Список использованной литературы.. 30
Введение
Сетевое планирование и управление (СПУ) – это комплекс графических и расчетных методов, организационных мероприятий, обеспечивающих моделирование, анализ и динамическую перестройку плана выполнения сложных проектов и разработок, например таких как: разработка туристской услуги, исследование системы управления организацией, маркетинговое исследование, разработка стратегий организации и др.
Сетевое планирование предполагает выполнение следующих этапов:
1. Разрабатываются планы выполнения всех отдельных работ комплекса; определяется трудоемкость выполнения, необходимые трудовые и иные ресурсы.
2. Устанавливается взаимосвязь работ и их относительный порядок выполнения.
3. Формируются события и присваиваются им номера по рассмотренным ранее правилам. Результаты выполнения этапов оформляются в виде таблицы
4. Составляется сетевой график (модель) по соответствующим правилам.
5. Выполняется расчет всех параметров сети и определяется критический путь.
6. Выполняется анализ сети. По коэффициентам напряженности и резервам времени классифицируются пути и работы.
7. Выполняется оптимизация сети – частная или комплексная по одному из критериев. При использовании частного критерия «минимум времени выполнения всего комплекса работ» определяется возможность сокращения продолжительности работ критического пути за счет ненапряженных путей – перераспределение ресурсов (перевод части работников на работы критического пути), т.е. проводится варьирование количества работников для работ ненапряженных и критического пути.
Основная цель сетевого планирования- сокращение до минимума продолжительности проекта.
Задача сетевого планирования состоит в том, чтобы графически, наглядно и системно отобразить и оптимизировать последовательность и взаимозависимость работ, действий или мероприятий, обеспечивающих своевременное и планомерное достижение конечных целей. Для отображения и алгоритмизации тех или иных действий или ситуаций используются экономико-математические модели, которые принято называть сетевыми моделями, простейшие из них - сетевые графики. С помощью сетевой модели руководитель работ или операции имеет возможность системно и масштабно представлять весь ход работ или оперативных мероприятий, управлять процессом их осуществления, а также маневрировать ресурсами.
1 Теория сетевого планирования в менеджменте
1.1Сущность сетевого планирования и управления
Сетевое планирование и управление (СПУ) - система планирования и управления разработкой крупных народно-хозяйственных комплексов, научными исследованиями, конструкторской и технологической подготовкой производства новых видов изделий, строительством и реконструкцией, капитальным ремонтом основных фондов путём применения сетевых графиков. Система СПУ позволяет устанавливать взаимосвязь планируемых работ и получаемых результатов, более точно рассчитывать план, а также своевременно осуществлять его корректировку.
Сетевое планирование и управление включает три основных этапа:
1. Структурное планирование.
2. Календарное планирование.
3. Оперативное управление.
Структурное сетевое планирование начинается с разбиения проекта на четко определенные операции, для которых определяется продолжительность и необходимые ресурсы. Затем строится сетевая модель (сетевой график), которая представляет взаимосвязи работ проекта. Это позволяет детально анализировать все работы и вносить улучшения в структуру проекта еще до начала его реализации.
Календарное сетевое планирование предусматривает определение моментов времени начала и окончания каждой работы и другие временные характеристики сетевого графика. Это позволяет, в частности, выявлять критические операции и пути сетевой модели, которым необходимо уделять особое внимание, чтобы закончить проект в директивный срок. Во время календарного планирования определяются все временные характеристики всех работ и событий с целью оптимизациисетевой модели, которая позволит улучшить эффективность использования какого-либо ресурса (трудовых ресурсов, времени, денежных средств и др.).
В ходе оперативного сетевого управления используются оптимизированный сетевой график и календарные сроки для составления периодических отчетов о ходе выполнения проекта. При этом модель может подвергаться оперативной корректировке, вследствие чего будет разрабатываться новые параметры остальной части сетевой модели.
Сетевая модель представляет собой описание комплекса работ (комплекса операций, проекта). Под ним понимается всякая задача, для выполнения которой необходимо осуществить достаточно большое количество разнообразных действий. Это может быть и строительство здания, корабля, самолета, или создание любого другого сложного объекта, и разработка проекта этого сооружения, и собственно процесс построения планов реализации проекта.
Сетевая модель может быть представлена в графическом виде, в виде систем управлений или в виде таблиц.
1.2Элементы сетевой модели и их характеристики, правила построения
Элементами сетевой модели являются: работы, события, пути.
Работа – это либо любой активный трудовой процесс, требующий затрат времени и ресурсов и приводящий к достижению определенных результатов (событий), либо пассивный процесс не требующий затрат труда, но занимающий время, либо, наконец, связь между какими-то результатами работ (событиями), называемая фиктивной работой. Обычно действительные работы в сетевом графике обозначаются сплошными стрелками ( ), а фиктивные работы – пунктирными ( ).
Событие– это итог проведенных работ, который дает начало для дальнейших (последующих) работ. Событие не имеет продолжительности во времени. Событие, за которым начинается данная работа, называется начальнымдля данной работы; оно обозначается символом i. Событие, которое наступает после выполнения данной работы, называется конечным для данной работы; оно обозначается символом j.
В каждой сети имеются два крайних события – исходное и завершающее. Исходным называется событие в сети, не имеющее предшествующих событий и отражающее начало выполнения всего комплекса работ. Оно обозначается символом I. Завершающим называется событие, которое не имеет последующих событий и показывает достижение конечной цели выполнения комплекса работ. Оно обозначается символом К. В одно и то же событие может входить и выходить из него несколько видов работ.
Путь – это любая последовательность работ в сетевом графике, в котором конечное событие каждой работы совпадает с начальным событием следующей за ней работы. Если известна продолжительность каждой работы tij , то для каждого пути может быть вычислена его общее время выполнения – длина, т. е. общая сумма продолжительности всех работ пути ТLi .
В сетевом графике следует различать несколько видов путей:
1) полный путь – путь от исходного события до завершающего; полный путь с максимальной продолжительностью называется критическим путем Lкр ;
2) путь, предшествующий данному событию, – путь от исходного события до данного;
3) путь, следующий за данным событием, – путь от данного события до завершающего;
4) путь между событиями i и j;
5) подкритический путь – полный путь, ближайший по длительности к критическому пути;
6) ненагруженный путь – полный путь, длительность которого значительно меньше длительности критического пути.
Собственные характеристики работ
К собственным характеристикам работ относятся:
– ij – двойные индексы работ, указывают место работы в сетевой модели и взаимосвязь с другими работами и событиями; i – индекс события предшествующей началу работы; j – индекс события, последующего за окончанием работы;
– Qij – трудоемкость работы в человеко-часах или в человеко-днях;
– mij – количество исполнителей, человек;
– tij – продолжительность выполнения работы в часах (или днях);
продолжительность работы – величина переменная и вычисляемая:
tij = Qij / mij . (1)
Системные характеристики событий
К системным характеристикам событий относятся: номера (индексы) событий, ранние и поздние сроки наступления событий и резервы времени событий.
Номера событий – i или j ; система нумерации должна обеспечивать условия: для каждой работы индексы i, j должны быть в отношениях i j.
Ранний срок наступления события – Тpi – это время, которое необходимо для выполнения всех работ, предшествующих данному событию. Оно равно наибольшей из продолжительности путей, предшествующих данному событию.
Для исходного события Tpо = 0.
Для всех остальных событий
Тpi = max {Тpc .+ tci } или (2)
, (2,а)
где max – максимум берется по всем работам (ij) одного из предшествующих путей событию i (рис. 1);
с – индекс события (вместо i) в формуле (2), предшествующего событию i, для которого определяется Тpi .
с – индекс события I в формуле (2,а), для которого определяется Тpi .
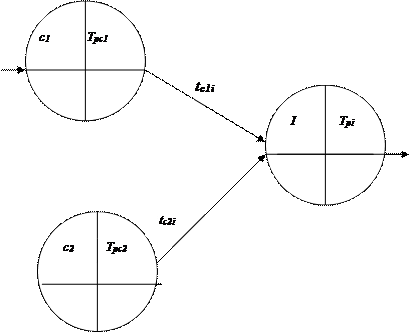
Рис.1 Схема расчета раннего срока 
наступления события i по формулам (2) и (2,а)
Поздний срок наступления события Tпi
– это такое время наступления события i
, превышение которого вызовет аналогичную задержку наступления завершающего события сети. Поздний срок наступления любого события равен разности между продолжительностью критического пути и наибольшей из продолжительности путей, следующих за событием i.
Поздние сроки свершения событий рассчитываются от текущего к завершающему событию. Для завершающего события 
, для всех остальных событий (рис. 2).
или (3)
, (3,а)
где 
- продолжительность критического пути;
с – текущее значение события i , для которого определяется поздний срок наступления события;
k – завершающее событие;
j – событие, последующее за событием i.
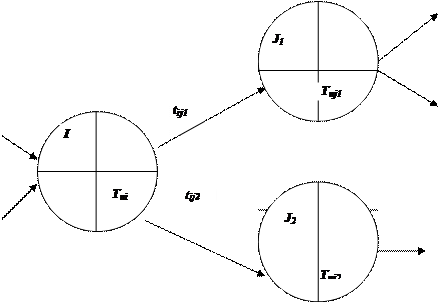
Рис.2 Расчет позднего срока Tni наступления события i по формулам (3) и (3,а)
Резерв времени наступления события Ri – это такой промежуток времени, на который может быть отсрочено наступление события i без нарушения сроков завершения проекта в целом. Начальные и конечные события критических работ имеют нулевые резервы событий.
(4)
Рассчитанные численные значения временных параметров событий допустимо записывать прямо в вершине сетевого графика (рис. 3).
 |
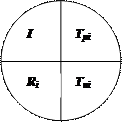Рис.3 Отображение временных параметров событий в вершинах сетевого графика
Системные характеристики работ
Rij
– полный резерв работы показывает, на какое время может быть увеличена продолжительность tij
отдельной работыij
, чтобы при этом 
- длина максимального из путей, проходящих через эту работу не превысила бы длины критического пути;
, (5)
- свободный резерв времени работы ij
– это та часть полного резерва, которая сохраняется у нее при условии, что конечное событие работы совершится в самый ранний срок, т.е. это резерв времени только данной работы, позволяющий увеличить ее продолжительность, не вызвав изменений ранних сроков совершения начального и конечного события остальных работ:
; (6)
Свободный резерв времени используются как вспомогательный параметр при необходимости более детального анализа конкретных ситуаций, возникающих в ходе выполнения работ;
- частный резерв времени работы ij
– это максимальный запас времени, на который можно задержать начало работы или (если она началась в ранний срок) увеличить ее продолжительность, не изменяя ранних сроков начала последующих работ:
; (7)
- независимый резерв времени работы ij
– это запас времени, при котором все предшествующие работы заканчиваются в поздний срок, а все последующие – начинаются в ранние сроки. Использование этого резерва не влияет на величину резервов времени других работ:
; (8)
Работы, лежащие на критическом пути, резервов времени не имеют;
- резерв трудовых ресурсов (исполнителей работ):
. (9)
Правила построения сетевой модели
Правило 1. Сеть имеет только одно начальное событие и только одно конечное событие.
Правило 2. Сеть вычерчивается слева направо. Желательно, чтобы каждое событие с большим порядковым номером изображалось правее предыдущего. Для каждой работы (i–j ) должно выполняться ij. Общее направление стрелок, изображающих работы, также должно быть расположено слева направо, при этом каждая работа должна выходить из события с меньшим номером и входить в событие с большим номером.
Правило 3. Если в процессе выполнения работы начинается другая работа, использующая результат некоторой части первой работы, то первая работа разбивается на две: причем часть первой работы от начала (0) до выдачи промежуточного результата, т. е. начало второй работы и оставшаяся часть первой работы, выделяются как самостоятельные.
Правило 4. Если «n» работ начинаются и кончаются одними и теми же событиями, то для установления взаимно-однозначного соответствия между этими работами и кодами необходимо ввести (n-1) фиктивных работ. Они не имеют продолжительности во времени и вводятся в данном случае лишь для того, чтобы упомянутые работы имели разные коды.
Правило 5. В сети не должно быть событий, в которые не входит ни одной работы, кроме исходного события. Нарушение этого правила и появление в сети, кроме исходного, еще одного события, в которое не входит ни одной работы, означает либо ошибку при построении сетевого графика, либо отсутствие (непланирование) работы, результат которой необходим для начала работы.
Правило 6. В сети не должно быть событий, из которых не выходит ни одной работы, кроме завершающего события. Нарушение этого правила и появление в сети, кроме завершающего, еще одного события, из которого не выходит ни одной работы, означает либо ошибку при построении сетевого графика, либо планирование ненужной работы, результат которой никого не интересует.
Правило 7. События следует нумеровать так, чтобы номер начального события данной работы был меньше номера конечного события этой работы.
Правило 8. В цепи не должно быть замкнутого контура.
Построение сети является лишь первым шагом на пути к построению календарного плана. Вторым шагом является расчет сетевой модели, который выполняют на сетевом графике, пользуясь простыми правилами и формулами ,или используют математическое представление сетевой модели в виде системы уравнений, целевой функции и граничных условий Третий шаг – оптимизация модели.
1.3 Оптимизация и критерии оптимизации
Оптимизация в широком смысле слова находит применение в науке, технике и в любой другой области человеческой деятельности.
Оптимизация - целенаправленная деятельность, заключающаяся в получении наилучших результатов при соответствующих условиях.
Поиски оптимальных решений привели к созданию специальных математических методов и уже в 18 веке были заложены математические основы оптимизации (вариационное исчисление, численные методы и др). Однако до второй половины 20 века методы оптимизации во многих областях науки и техники применялись очень редко, поскольку практическое использование математических методов оптимизации требовало огромной вычислительной работы, которую без ЭВМ реализовать было крайне трудно, а в ряде случаев - невозможно. Особенно большие трудности возникали при решении задач оптимизации процессов в химической технологии из-за большого числа параметров и их сложной взаимосвязи между собой. При наличии ЭВМ задача заметно упрощается.
Постановка задачи оптимизации предполагает существование конкурирующих свойств процесса, например:
- количество продукции - расход сырья
-количество продукции - качество продукции
Выбор компромиссного варианта для указанных свойств и представляет собой процедуру решения оптимизационной задачи.
При постановке задачи оптимизации необходимо:
1. Наличие объекта оптимизации и цели оптимизации. При этом формулировка каждой задачи оптимизации должна требовать экстремального значения лишь одной величины, т.е. одновременно системе не должно приписываться два и более критериев оптимизации, т.к. практически всегда экстремум одного критерия не соответствует экстремуму другого.
Типичный пример неправильной постановки задачи оптимизации:
Получить максимальную производительность при минимальной себестоимости.
Ошибка заключается в том, что ставится задача поиска оптимума 2-х величин, противоречащих друг другу по своей сути.
Правильная постановка задачи могла быть следующая:
а) получить максимальную производительность при заданной себестоимости;
б) получить минимальную себестоимость при заданной производительности;
В первом случае критерий оптимизации - производительность а во втором - себестоимость.
2. Наличие ресурсов оптимизации, под которыми понимают возможность выбора значений некоторых параметров оптимизируемого объекта. Объект должен обладать определенными степенями свободы - управляющими воздействиями.
3. Возможность количественной оценки оптимизируемой величины, поскольку только в этом случае можно сравнивать эффекты от выбора тех или иных управляющих воздействий.
4. Учет ограничений.
Обычно оптимизируемая величина связана с экономичностью работы рассматриваемого объекта (аппарат, цех, завод ). Оптимизируемый вариант работы объекта должен оцениваться какой-то количественной мерой-критерием оптимальности.
Критерием оптимальности называется количественная оценка оптимизируемого качества объекта.
На основании выбранного критерия оптимальности составляется целевая функция, представляющая собой зависимость критерия оптимальности от параметров, влияющих на ее значение. Вид критерия оптимальности или целевой функции определяется конкретной задачей оптимизации.
Таким образом, задача оптимизации сводится к нахождению экстремума целевой функции.
Наиболее общей постановкой оптимальной задачи является выражение критерия оптимальности в виде экономической оценки (производительность, себестоимость продукции, прибыль, рентабельность).Однако в частных задачах оптимизации, когда объект является частью технологического процесса, не всегда удается или не всегда целесообразно выделять прямой экономический показатель, который бы полностью характеризовал эффективность работы рассматриваемого объекта. В таких случаях критерием оптимальности может служить технологическая характеристика, косвенно оценивающая экономичность работы агрегата (время контакта, выход продукта, степень превращения, температура). Но в любом случае любой критерий оптимальности имеет экономическую природу.
Критерий оптимальности должен иметь ясный физический смысл ,отражать наиболее существенные стороны процесса , должен иметь количественную оценку.
В том случае, когда случайные возмущения невелики и их воздействие на объект можно не учитывать, критерий оптимальности может быть представлен как функция входных, выходных и управляющих параметров: R=R(X1, X2,...,XN, Y1,Y2,...,YN, U1,U2,..., UN)
Так как Y=f (U), то при фиксированных Х можно записать: R=R( U1,U2,..., UN)
При этом всякое изменение значений управляющих параметров двояко сказывается на величине R:
- прямо, так как управляющие параметры непосредственно входят в выражение критерия оптимизации;
- косвенно - через изменение выходных параметров процесса, которые зависят от управляющих.
Как правило, для конкретных задач оптимизации химических производств критерий оптимальности не может быть записан в виде аналитического выражения.
В принципе, для оптимизации вместо математической модели можно использовать и сам объект, однако оптимизация опытным путем имеет ряд существенных недостатков:
а) необходим реальный объект;
б) необходимо изменять технологический режим в значительных пределах, что не всегда возможно;
в) длительность испытаний и сложность обработки данных. Наличие математической модели (при условии, что она достаточно надежно описывает процесс) позволяет значительно проще решить задачу оптимизации аналитическим либо численным методами.
Итак, для решения задачи оптимизации необходимо:
а) составить математическую модель объекта оптимизации,
б) выбрать критерий оптимальности и составить целевую функцию,
в) установить возможные ограничения, которые должны накладываться на переменные,
г) выбрать метод оптимизации, который позволит найти экстремальные значения искомых величин.
Классификация задач оптимизации.
Принято различать задачи статической оптимизации для процессов, протекающих в установившихся режимах, и задачи динамической оптимизации.
В первом случае решаются вопросы создания и реализации оптимальной модели процесса, во втором -задачи создания и реализации системы оптимального управления процессом при неустановившихся режимах эксплуатации.
Если требуется определить экстремум целевой функции без задания условий на какие-либо другие величины, то такая оптимизация называется безусловной. Такие критерии обычно используются при решении частных задач оптимизации (например, определение максимальной концентрации целевого продукта, оптимального времени пребывания реакционной смеси в аппарате и т.п.).
Если необходимо установить экстремум целевой функции при некоторых условиях, которые накладываются на ряд других величин (например, определение максимальной производительности при заданной себестоимости, определение оптимальной температуры при ограничениях по термостойкости катализатора и др.), то такая оптимизация называется условной.
Процедура решения задачи оптимизации обязательно включает, помимо выбора управляющих параметров, еще и установление ограничений на эти параметры (термостойкость, взрывобезопасность, мощность перекачивающих устройств).
Ограничения могут накладываться как по технологическим, так и по экономическим соображениям.
В зависимости от управляющих параметров различают следующие задачи :
· оптимизация при одной управляющей переменной - одномерная оптимизация,
· оптимизация при нескольких управляющих переменных – многомерная оптимизация,
· оптимизация при неопределённости данных,
· оптимизация с непрерывными ,дискретными и смешанным типом значений управляющих воздействий.
В зависимости от критерия оптимизации различают:
· с одним критерием оптимизации- критерий оптимальности единственный.
· со многими критериями. Для решения задач со многими критериями используются специальные методы оптимизации.
1.4. Область использования сетевой модели
Первые системы, использующие сетевые графики, были разработаны и применены в США в конце 50-х годов XX века и получили название CPM (английская аббревиатура – метод критического пути) и PERT – (метод оценки и обзора программы). Система CPM впервые была применена при управлении строительными работами, система PERT – при разработке системы «Поларис».
В Советском Союзе работы по сетевому планированию стали появляться в 60-х годах XX века. Тогда методы СПУ нашли применение в строительстве и научных разработках. В дальнейшем сетевые методы стали широко применяться и в других областях народного хозяйства.
Система СПУ позволяет:
· формировать календарный план реализации некоторого комплекса работ;
· выявлять и мобилизовывать резервы времени, трудовые, материальные и денежные ресурсы;
· осуществлять управление комплексом работ по принципу «ведущего звена» с прогнозированием и предупреждением возможных срывов в ходе работ;
· повышать эффективность управления в целом при четком распределении ответственности между руководителями разных уровней и исполнителями работ.
Диапазон применения СПУ весьма широк: от задач, касающихся деятельности отдельных лиц, до проектов, в которых участвуют сотни организаций и десятки тысяч людей (разработка и создание крупного территориально-производственного комплекса).
2 Построение и оптимизация сетевой модели
2.1 Исходные данные для построения сетевой модели
| № | Обозначение работ i-j | Qi-j | Wi-j | № | Обозначение работ i-j | Qi-j | Wi-j |
| 1 | 0-1 | 20 | 5 | 11 | 5-10 | 16 | 4 |
| 2 | 0-2 | 40 | 10 | 12 | 5-13 | 16 | 4 |
| 3 | 0-3 | 10 | 2 | 13 | 6-11 | 6 | 1 |
| 4 | 0-4 | 20 | 2 | 14 | 7-11 | 40 | 1 |
| 5 | 1-5 | 12 | 3 | 15 | 8-3 | 0 | 0 |
| 6 | 1-6 | 16 | 4 | 16 | 9-12 | 30 | 5 |
| 7 | 2-7 | 0 | 0 | 17 | 10-13 | 20 | 5 |
| 8 | 3-7 | 20 | 1 | 18 | 11-13 | 10 | 1 |
| 9 | 4-8 | 20 | 1 | 19 | 12-14 | 16 | 4 |
| 10 | 4-9 | 12 | 2 | 20 | 13-14 | 10 | 1 |
Qi-j – трудоемкость работы в человекоднях;
Wi-j – Количество исполнителей (количество человек);
i– индекс предшествующего события;
j – индекс последующего события.
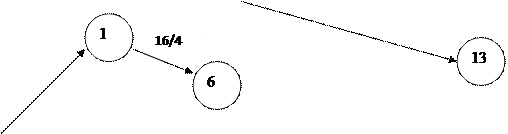
2.2 Графическое изображение сетевой модели.
 |
|
|
|
|
|
|
|
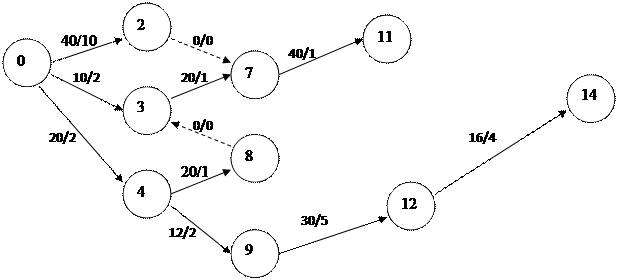
2.3 Анализ сетевой модели и определение критического пути
Найдем продолжительность каждой работы по формуле: 
.
t0-1 =20/5=4 t1-6 =16/4=4 t5-10 =16/4=4 t9-12 = 30/5=6
t0-2 =40/10=4 t2-7 =0 t5-13 =16/4=4 t10-13 = 20/5=4
t0-3 =10/2=5 t3-7 =20/1=20 t6-11 =6/1=6 t11-13 = 10/1=10
t0-4 =20/2=10 t4-8 =20/1=20 t7-11 =40/1=40 t12-14 = 16/4=4
t 1-5 =12/3=4 t4-9 =12/2=6 t8-3 = 0 t13-14 =10/1=10
Теперь отметим все возможные пути:
Путь L1 = 0 – 1 – 5 – 10 – 13 – 14
Путь L2 = 0 – 1 – 5 – 13 – 14
Путь L3 = 0 – 1 – 6 – 11 – 13 – 14
Путь L4 = 0 – 2 – 7 – 11 – 13 – 14
Путь L5 = 0 – 3 – 7 – 11 – 13 – 14
Путь L6 = 0 – 4 – 8 – 3 – 7 – 11 – 13 – 14
Путь L7 = 0 – 4 – 9 – 12 – 14
Возможных путей семь. Произведем расчеты, с помощью которых вычислим продолжительности каждого пути. Для этого воспользуемся формулой:
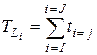, где ti
-
j
– продолжительности работ данного пути (в часах).
TL 1 =4+4+4+4+10=26
TL 2 =4+4+4+10=22
TL 3 =4+4+6+10+10=34
TL 4 =4+0+40+10+10=64
TL 5 =5+20+40+10+10=85
TL 6 =10+20+0+20+10+10=110
TL 7 =10+6+6+4=26
Выделим критический путь L кр . Путь с наибольшей продолжительностью по времени будет являться критическим. Это путь L 6 с продолжительностью TL 6 =110 часов. Путь с наименьшей продолжительностью по времени будет являться ненагруженным. Это путь L 2 с продолжительностью TL 2 =22 часа.
2.4 Расчеты собственных системных характеристик элементов
Найдем среднее значение продолжительности пути 
. Для этого воспользуемся формулой 
, где n – количество путей. Тогда TLcp
=
367/7=52,43 (часа).
Имея величину TLcp рассчитаем резерв времени RLi для каждого пути Li . Резерв времени вычисляется по формуле RL = TLcp - TLi . Данные о продолжительности путей и резервах времени по путям приведены в таблице.
Исходные продолжительности и резервы пути.
| Путь Ц | TL , (в часах) | RL (в часах) |
| 1 | 26 | 26,43 |
| 2 | 22 | 30,43 |
| 3 | 34 | 18,43 |
| 4 | 64 | -11,57 |
| 5 | 85 | -32,57 |
| 6 | 110 | -57,57 |
| 7 | 26 | 26,43 |
Отрицательные значения RL 1, RL 2, RL 3 свидетельствуют о том, что эти пути критические и условный дефицит времени составляет 33,2; 7,2; 1,2 часа соответственно.
Рассчитаем характеристики событий. При определении ранних сроков наступления событий Т
pi
двигаемся по сетевому графику слева направо и используем форму Тpi
= max {Тpc
.+ tci
} , при определении поздних сроков наступления событии Тп
i
двигаемся по сетевому графику справа налево и используем формулы 
или 
Ранние и поздние сроки наступления событий
Ранние сроки наступления событий - Тpi :
Тр0 =0
Т р1(0-1) =4
Т р2(0-2) =4
Т р3(0-3) =5
Т р4(0-4) =10
Т р5(0-1-5) =4+4=8
Т р6(0-1-6) =4+4=8
Т р7(0-4-8-3-7) =10+20+0+20=50
Т р8(0-4-8) =10+20=30
Т р9(0-4-9) =10+6=16
Т р10(0-1-5-10) =4+4+4=12
Т р11(0-4-8-3-7-11) =10+20+0+20+40=90
Т р12(0-4-9-12) =10+6+6=22
Т р13(0-4-8-3-7-11-13) =10+20+0+20+40+10=100
Т р14(0-4-8-3-7-11-13-14) =10+20+0+20+40+10+10=110
Поздние сроки наступления событий Тп i :
Т п0 =0
Т п1(1-6-11-13-14) =110-(4+6+10+10)=110-30=80
Т п2(2-7-11-13-14) =110-(0+40+10+10)=50
Т п3(3-7-11-13-14) = 110-(20+40+10+10)=110-80=30
Т п4(4-8-3-7-11-13-14) =110-(20+0+20+40+10+10)=110-100=10
Т п5(5-10-13-14) =110-(4+4+10)=110-18=92
Т п6(6-11-13-14) =110-(6+10+10)=110-26=84
Т п7(7-11-13-14) =110-(40+10+10)=110-60=50
Т п8(8-3-7-11-13-14) =110-(0+20+40+10+10)=110-80=30
Т п9(9-12-14) =110-(6+4)=110-10=100
Т п10(10-13-14) =110-(4+10)=110-14=96
Т п11(11-13-14) =110-(10+10)=110-20=90
Т п12(12-14) =110-4=106
Т п13(13-14) =110-10=100
Т п14 =110-0=110
| Событие Lt | Тр i | Тп i |
| 0 | 0 | 0 |
| 1 | 4 | 80 |
| 2 | 4 | 50 |
| 3 | 5 | 30 |
| 4 | 10 | 10 |
| 5 | 8 | 92 |
| 6 | 8 | 84 |
| 7 | 50 | 50 |
| 8 | 30 | 30 |
| 9 | 16 | 100 |
| 10 | 12 | 96 |
| 11 | 90 | 90 |
| 12 | 22 | 106 |
| 13 | 100 | 100 |
| 14 | 110 | 110 |
Вычислим максимальный запас времени, на который можно отсрочить начало или увеличить длительность каждой работ без увеличения длительности критического пути. Этот запас называется свободным резервом времени работы и обозначается Rcij
.
Для этого воспользуемся формулой 
Работы на критическом пути не имеют полного резерва времени, для них Ri - j = 0, тогда получаем, что
| R 0-1 =80-0-4=76 | R 5-10 =96-8-4=84 |
| R 0-2 =50-0-4=46 | R 5-13 =100-8-4=88 |
| R 0-3 =30-0-5=25 | R 6-11 =90-8-6=76 |
| R 0-4 =10-0-10=0 | R 7-11 =90-50-40=0 |
| R 1-5 =92-4-4=84 | R 8-3 =30-30-0=0 |
| R 1-6 =84-4-4=76 | R 9-12 =106-16-6=84 |
| R 2-7 =50-4-0=46 | R 10-13 =100-12-4=84 |
| R 3-7 =50-5-20=25 | R 11-13 =100-90-10=0 |
| R 4-8 =30-10-20=0 | R 12-14 =110-22-4=84 |
| R 4-9 =100-10-6=84 | R 13-14 =110-100-10=0 |
2.5 Алгоритм оптимизации сетевой модели
Количество исполнителей ml
-
j
, которых возможно снять с работ, вычислим по формуле 
.
m 0-1 (р)=5-(20/(4+0,5*76))=5-20/42=4
m 0-2 (р)=10-(40/(4+0,5*46))=10-1,5=9
m 0-3 (р)=2-(10/(5+0,5*25))=2-0,57=1
m 0-4 (р)=2-(20/(10+0,5*0))=2-2=0
m 1-5 (р)=3-(12/(4+0,5*84))=3-0,26=2
m 1-6 (р)=4-(16/(4+0,5*76))=4-0,38=3
m 2-7 (р)=0
m 3-7 (р)=1-(20/(20+0,5*25))=1-0,61=0
m 4-8 (р)=1-(20/(20*0,5*0))=1-1=0
m 4-9 (р)=2-(12/(6+0,5*84))=2-0,25=1
m 5-10 (р)=4-(16/(4+0,5*84))=4-0,34=3
m 5-13 (р)=4-(16/(4+0,5*88))=4-0,33=3
m 6-11 (р)=1-(6/(6+0,5*76))=1-0,13=0
m 7-11 (р)=1-(40/(40+0,5*0))=1-1=0
m 8-3 (р)=0
m 9-12 (р)=5-(30/(6+0,5*84))=5-0,6=4
m 10-13 (р)=5-(20/(4+0,5*84))=5-0,43=4
m 11-13 (р)=1-(10/(10+0,5*0))=1-1=0
m 12-14 (р)=4-(16/(4+0,5*84))=4-1,26=3
m 13-14 (р)=1-(10/(10+0,5*0))=1-1=0
2.6 Результат оптимизации
Из возможных вариантов mi - j выберем работы i - j , с которых наиболее удобно снять исполнителей. Для этого мы проведем оптимизацию данного проекта безмашинным способом, переставляя исполнителей с ненагруженных путей Li наработы i - j критического пути L кр . Перестановки исполнителей и результаты оптимизации отражены в таблице «Результаты перераспределения трудовых ресурсов (исполнителей)», где
Qi - j – трудоемкость работы в человекоднях.
mi-j – количество исполнителей.
t i - j – продолжительность работы в днях.
mi - j –количество человек, добавленных на выполнение данной операции.
mi - j – количество человек, убранных с выполнения данной операции.
m i - j – количество исполнителей после оптимизации.
ti - j – продолжительность работы в днях после оптимизации.
Результаты перераспределения трудовых ресурсов (исполнителей)
| i-j | Qi-j | mi-j | ti-j | mi - j | mi - j | m i - j | t i - j |
| 0-1 | 20 | 5 | 4 | 3 | 2 | 10 | |
| 0-2 | 40 | 10 | 4 | 6 | 4 | 10 | |
| 0-3 | 10 | 2 | 5 | 2 | 5 | ||
| 0-4 | 20 | 2 | 10 | 3 | 5 | 4 | |
| 1-5 | 12 | 3 | 4 | 2 | 1 | 12 | |
| 1-6 | 16 | 4 | 4 | 4 | 4 | ||
| 2-7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 3-7 | 20 | 1 | 20 | 3 | 4 | 5 | |
| 4-8 | 20 | 1 | 20 | 8 | 9 | 2,2 | |
| 4-9 | 12 | 2 | 6 | 1 | 1 | 12 | |
| 5-10 | 16 | 4 | 4 | 4 | 4 | ||
| 5-13 | 16 | 4 | 4 | 2 | 2 | 8 | |
| 6-11 | 6 | 1 | 6 | 1 | 6 | ||
| 7-11 | 40 | 1 | 40 | 3 | 4 | 10 | |
| 8-3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 9-12 | 30 | 5 | 6 | 3 | 2 | 15 | |
| 10-13 | 20 | 5 | 4 | 5 | 4 | ||
| 11-13 | 10 | 1 | 10 | 1 | 10 | ||
| 12-14 | 16 | 4 | 4 | 1 | 3 | 5,3 | |
| 13-14 | 10 | 1 | 10 | 1 | 2 | 5 |
Определим новую продолжительность времени выполнения всех работ каждого пути после оптимизации (в часах)
Путь L1 (0 – 1 – 5 – 10 – 13 – 14)
Путь L2 (0 – 1 – 5 – 13 – 14)
Путь L3 (0 – 1 – 6 – 11 – 13 – 14)
Путь L4 (0 – 2 – 7 – 11 – 13 – 14)
Путь L5 (0 – 3 – 7 – 11 – 13 – 14)
Путь L6 (0 – 4 – 8 – 3 – 7 – 11 – 13 – 14)
Путь L7 (0 – 4 – 9 – 12 – 14)
TL 1 =10+12+4+4+5=35
TL 2 =10+12+8+5=35
TL 3 =10+4+6+10+5=35
TL 4 =10+0+10+10+5=35
TL 5 =5+5+10+10+5=35
TL 6 =4+2,2+0+5+10+10+5=36,2
TL 7 =4+12+15+5,3=36,3
Для удобства сравнения продолжительности путей исходной сетевой модели с продолжительностью путей оптимизированной сетевой модели обратимся к таблице
Системные характеристики исходной и оптимизированной сетевой модели
| Путь Li | TLi (в часах) | T’Li (в часах) |
| 1 | 26 | 35 |
| 2 | 22 | 35 |
| 3 | 34 | 35 |
| 4 | 64 | 35 |
| 5 | 85 | 35 |
| 6 | 110 | 36,2 |
| 7 | 26 | 36,3 |
| 367 | 247,5 | |
| Lcp | 52,4 | 35,4 |
Общее время выполнения комплекса работ сократилось почти в 1,5 раза.
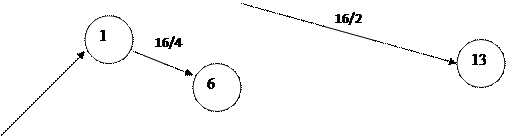
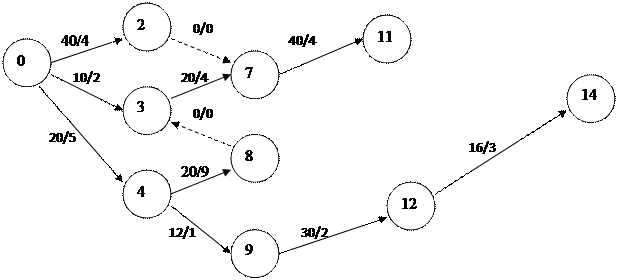
2.7 Сетевая модель после оптимизации
 |
|
|
|
|
|
|
Заключение
В результате можно сделать вывод, что сетевая модель используется для выработки управленческих решений, которые содержат сведения о выполняемых работах, как управленческих, так и исполнительских. Модель позволяет получить для всего комплекса планируемых работ сроки выполнения, стоимость работ, предпочтительный маршрут движения, объем необходимых ресурсов и прогноз развития ситуации.
Проведенная оптимизация привела к:
· сокращению времени выполнения работ;
· сокращению стоимости работ;
· определению позднего срока начала работ, если известен конечный срок;
· к более грамотному распределению количества исполнителей на работах.
Результаты сетевого планирования могут быть использованы на предприятиях при разработке годовых планов технико-экономической, социально-трудовой, финансово-инвестиционной и всех других видов рыночной деятельности.
Список использованной литературы
1. А.В. Ключников. Менеджмент в туризме.- Советский спорт, 2009;
2. Дж.Модер,С. Филипс, Метод сетевого планирования в организации работ, пер. с англ., М.- Л., 1966;
3. Н.М. Губин,А.С. Добронравов,Б.С. Дорохов.-Экономико-математические методы и модели в планировании и управлении в отрасли связи. - М.: Радио и связь, 1993;
4. С. И. Зуховицкий, И.А. Радчик, Математические методы сетевого планирования, М., 1965;
5. Х. Таха. Введение в исследование операций. - М.: Мир, 1985.