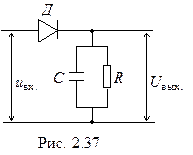Шпаргалка по Физике 3

СОДЕРЖАНИЕ: Билет 1 Вопрос 35 Магнитное поле и его характеристики В результате многочисленных экспериментальных исследований (Эрстед, Ампер и другие) было установлено, что проводники с током проявляют свойства, близкие свойствам постоянных магнитов. Подобно магниту, проводник с током оказывает ориентирующее действие на магнитную стрелку.

Билет 1 Вопрос 35 Магнитное поле и его характеристики

В результате многочисленных экспериментальных исследований (Эрстед, Ампер и другие) было установлено, что проводники с током проявляют свойства, близкие свойствам постоянных магнитов. Подобно магниту, проводник с током оказывает ориентирующее действие на магнитную стрелку. Подвешенная на тонкой нити катушка с током ориентируется, как и стрелка компаса, вдоль магнитного меридиана Земли. Опытным путем можно удостовериться, что взаимодействие двух катушек с током тождественно взаимодействию двух прямых магнитов. По этой причине взаимодействие проводников с током называют магнитным взаимодействием. Это взаимодействие не может быть обусловлено электрически полем, поскольку проводники с током электрически нейтральны. Его можно объяснить, если предположить, что токи порождают в окружающем пространстве особый вид материи – магнитное поле, посредством которого и осуществляются взаимодействия между проводниками с током. Поскольку электрический ток обусловлен движением заряженных частиц, отсюда следует, что магнитное поле порождается движущимися зарядами и действует только на движущиеся заряды . Для описания магнитного поля вводится векторная характеристика, которая называется индукцией магнитного поля (магнитной индукцией) и обозначается буквой . Экспериментально установлено, что для магнитных полей, как и для электрических, выполняется принцип суперпозиции : при наложении нескольких магнитных полей индукция результирующего поля равна векторной сумме индукций этих полей: Поскольку магнитное поле действует на токи, это поле можно исследовать с помощью очень малых контуров (петель) с током. Ориентацию такого малого плоского контура с током в пространстве будем описывать, указывая направление положительной нормали к контуру (т.е. нормали, связанной с направлением тока в контуре правилом правого винта ), как показано на рис 1.1. Если такой пробный контур с током поместить в магнитное поле, он установится положительной нормалью в некотором направлении. Это направление и принимается за направление вектора магнитной индукции в той точке пространства, в которую помещен пробный контур. Если после этого контур повернуть, то возникает вращающий момент, который стремится вернуть контур в исходное равновесное положение. Величина этого момента максимальна, когда . Кроме того, величина вращательного момента М пропорциональна произведению IS , где I – сила тока в контуре,S – его площадь. Опыт свидетельствует, что величина отношения

(1.2)

не зависит от формы контура, площади и силы тока и является характеристикой поля в данной точке. Оно принимается в качестве модуля вектора .

Единицей магнитной индукции является тесла (Тл).

Вопрос 70 Колебательный контур. Свободные электрические колебания. Системой, в которой могут происходить собственные электромагнитныеколебания, является колебательный контур, представляющий собой последовательно соединенные конденсатор емкостьюС , катушку индуктивности L и резистор с активным сопротивлением R . Контур обладает энергией электрического поля и энергией магнитного поля катушки индуктивности: . Т.кв идеальном контуре мы пренебрегаем потерями энергии, из закона сохранения энергии имеем: ,отсюда находим максимальное значение силы тока в контуре: Электромагнитными колебаниями называют периодическое изменение произвольных величин (токов, зарядов, напряжений), характеризующих процессы, протекающие в цепях переменного тока . Электромагнитные колебания, протекающие в результате процессов, происходящих в самой цепи без влияния на нее извне, называются собственными электромагнитными колебаниями . Собственные электромагнитные колебания протекают в цепях, не содержащих источников переменного тока. Электромагнитные колебания возникают по причине явления самоиндукции.

Білет 2 Вопрос 17

Энергия конденсатора. W=CU² \2. dA=dqU;dq=CdU; dA=CUdU; W=CU² \2

U=c\q, то W= qu\2 Энергияэл.поля E=qU

Вопрос 45

Поскольку всякий ток есть направленное движение заряженных частиц, отсюда следует , что на движущуюся в магнитном поле заряженную частицу действует сила ЛоренцаF=qVBsin(V,B) Сила Лоренца всегда перпендикулярна скорости частицы. При движении в стационарном магнитном поле не изменяется кинетическая энергия частицы, а ее скорость меняется только по направлению. Направлениеопределяется по правилу буравчика.

При движении частицы модуль ее скорости остается неизменным, неизменным остается и величина силы Лоренца. Эта сила будет центростремительной, движение будет по окружности (перпендикулярно влетающая частица). Радиус этой окружности, приравнивая центростремительную силу силе Лоренца будет равен r = Если частица имеющая начальную скорость влетает в магнитное поле под некоторым углом к магнитной индукции В, то V можно разложить на две составляющие параллельную Перпендикуляр. При парал. Движении изменяться не будет, а перпендик. Составляющая скорости будет менять лишь направление, по величине оставаясь равной Частица будет двигаться по спирали.

Білет 3

Вопрос 41 З-н Ампера

На элемент тока, находящегося в магнитном поле действует сила F=IBlsin. Пименяется для определения силы взаимодействия двух токов. Сила действующая на элемент тока, всегда перпендикулярна элементу тока и вектору магнитной индукции. Направление F можно определить с помощью правила левой руки. В-в ладонь,I-4 пальца, F-большой палец.

Вопрос 11

Диэлектрики – вещества плохо проводящие ток, т.к. они не имеют свободных молекул. Молекулы плотно связаны с самим зарядом. Диэлектрики бывают полярные(центры зарядов не совпадают ) и неполярные( центры зарядов не совпадают) Дипольные моменты. Диполь – два точечных заряда находящихся на расстоянии друг от друга. p=ql – дипольный момент(основнаяхарактеристика диполя) Однородное поле: силы стремятся сорентировать диполь по полю M=qElsin; Eq=-Eq но противоположны по направлению. Неоднородное поле: Eq не равно –Eq и не равно 0. Диполь сорентирован по полю.

Билет 4 Вопрос 25

Рассмотрим вырывание электронов из находящегося в вакууме куска металла. Электроны проводимости удерживаются внутри металла вследствие того, что вблизи поверхности на электроны не действуют силы, направленные вглубь металла. Чтобы электрон мог покинуть металл, нужно совершить работу против этих сил. Эта работа называется работой выхода электрона из металла. Она различна для разных металлов. Наличие этой работы показывает, что в поверхностном слое металла существует электрическое поле, препятствующее выходу электрона. Следовательно в этом слое потенциал изменяется на некоторую величину которая также является характеристикой металла. Она называется поверхностной разностью потенциала, связана с работой выхода соотношением

Условие выхода электрона из металла: Работа выхода электрона из металла имеет величину в несколько электронвольт. 1 электронвольт – энергия, которую приобретает электрон, пройдя ускоряющую разность потенциалов в 1 В. 1 эВ= 1,6*10^-19 Дж. Приведём в соприкосновение два различных металла, имеющих одинаковую температуру. Электроны проводимости будут диффундировать из одного металла в другой. Поскольку их концентрация в проводниках различна, потоки электронов будут различны и металл с большей концентрациейэлектронов будет заряжаться положительно, а с меньшей – отрицательно. В результате между проводниками возникнет разность потенциалов и появиться поле, препятствующее движению электронов от металла с большей концентрацией к металлу с их меньшей концентрацией. При достижении некоторой равности потенциалов U_и между металлами установиться равновесное состояние системы электронов. Эта разность и называется внутренней контактной разностью потенциалов. Электрическое поле, порождаемое контактной разностью , сосредоточено в тонком пограничном слое между проводниками.

Вопрос 58 Энергия магнитного поля.

Проводник по которому течет ток, всегда окружен магнитным полем, причем магнитное поле появляется и исчезает вместе с появлением и исчезновением тока. Магнитное поле является носителем энергии. Энергия магнитного поля равна работе, которая затрачивается током на создание этого поля.

Рассмотрим контур индуктивностью L, по которому течет ток I. С данным контуром сцеплен магнитный поток (см рис) Ф=LI,причем при изменении тока на dI магнитный поток изменяется на dФ=LdI. Однако для изменения магнитного потока на величину dФ необходимо совершить работу dA=IdФ=LIdI. Тогда работа по созданию магнитного потока Ф будет равнаA= интегралу от 0 до ILIdI=LI² /2.Энергия магнитного поля связанного с контуром равна W=LI² /2 .

Энергия магн. поля локализована в пространстве.Энергиямагн. поля можно представить как функцию величин, характеризующихэто поле в окружающем пространстве.Расмотримчастнсл – однородное магн поле внутри длинного соленоида. Подставив в формулу W=LI² /2выражение L=0N² S/, получим W= 0N² I² S/2Так как I=B/(₀ N ) и B=₀ H, то W=B² V/2₀ =BHV/2, где S=V – объем соленоида.магн. поля соленоида однородно и сосредоточено внутри его , поэтому энергия заключена внутри соленоида и распределена в немс постоянной объемной плотностью: =W/V=B² /2₀ = ₀ H² /2=BH/2

Билет 5 Вопрос 3 Работа электрического поля. Разность потенциалов.

На электрический заряд q со стороны поля, созданного зарядом Q,действует кулоновская сила. Поэтому при перемещении заряда q в поле совершается работа, величина которой определяется выражением dA = Fldlcosa, где a - угол между направлениями силы и перемещения .Учитывая, что Fcosa = Fl имеем dA = Fldl. Для нашего случая F = qE;

A₁₂ (L₁ ) – A₂₁ (L₂ ) = q ( E* d₁ - E* d₂ ) = q ( E* d₁ + E* d^’ ₂ ) =q. Так каквыражение в скобках последнего выражения есть равная нулю циркуляция вектора напряженности эл. Поля, то А₁₂ (L₁ )= А₁₂ (L₂ ) Разностью потенциалов(напряжением) между двумя точками в электростатическом поле называется работа, совершаемая полем при перемещении единичного полож. заряда между этими точками: U₁₂ = E*d Если разность потенциалов точек известна, легко найти работу, совершаемую силами поля при перемещении произвольного зарядаq между этими точками: A₁₂ =q*U₁₂

Потенциал – величина скалярная, он удовлетворяет принципу суперпозиции, т.е. потенциал от суммы зарядов равен сумме потенциалов от каждого заряда в отдельности. Единица напряжения: А=1Дж, q=1Кл U₁₂ =1 Дж/Кл - Вольт. При перемещении произвольного заряда q величина совершаемой работы увеличивается в q раз.Работа через изм. Потенц. Энергии :A₁₂ =q(₁ - ₂ )=q₁ -q₂ =П₁ -П_2.

Вопрос 60 Уравнения Максвелла в интегральной форме Выпишем уже известные нам соотношения, определяющие поток и циркуляцию основных () и вспомогательных () характеристик электрического и магнитного поля:

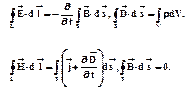(1.107)

Эти соотношения были положены Максвеллом в основу электродинамики – единой теории электрических и магнитных явлений, и называются уравнениями Максвелла в интегральной форме. Одних уравнений Максвелла недостаточно для нахождения характеристик поля по заданным распределениям плотности свободных зарядов r и плотности тока проводимости . Их еще необходимо дополнить соотношениями, связывающими ,, :

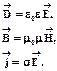(1.108)

где s – удельная проводимость вещества. Эти соотношения называют материальными уравнениями. Дополненная материальными уравнениями, система уравнений Максвелла описывает всю совокупность электромагнитных явлений в неподвижных средах.

Билет 6 Вопрос 40 Магнитное поле соленоида

Соленоид представляет собой полый цилиндр, на который плотно намотан провод. если витки соленоида плотно прилегают друг к другу, а длина значительно превышает его поперечные размеры, картина линий магнитной индукции поля соленоида при пропускании через него тока выглядит так рис. 1.12. Внутри соленоида поле однородно везде, кроме областей вблизи его краев. Индукция магнитного поля вне соленоида значительно меньше по модулю индукции поля внутри соленоида. Поскольку линии магнитной индукции всегда замкнуты, число линий внутри соленоида равно числу линий, проходящих снаружи. Но снаружи линии распределены по всему неограниченному пространству вне соленоида, поэтому их густота гораздо меньше. алгебраическая сумма токов, пронизывающих контур L , равна S I _k = n l I . гдеl – длина стороны контура, параллельной . Пренебрегая индукцией поля вне соленоида учитывая, что на боковых сторонах контура (поэтому ), будем иметь B l = m _o n l I откудаB = m _o n I . индукция магнитного поля внутри соленоида определяется величиной nI , которая называется числом ампер-витков на метр .

Вопрос 13

Общее поле E=E^/ +E₀ ;E₀ – поле свободных зарядов E^/ - поле диэлекрика. D=₀ – смещение; D – описывает поле создаваемое свободным зарядом. P=x₀ ; x – характеристика поля. D=₀ +P; D=₀ +₀ x;D=₀ (x+1); x+1=;D=₀

Билет 7 Вопрос 14

Проводники – в-ва хорошо проводящие ток, т.к. имеют свободные заряды. Малая сила действующая на эти заряды приводит их в движение.При этом происходит перераспределение зарядов.

Св-ва:1.Напряженность эл. поля внутри проводника = 0. 2.E перпендикулярна поверхности проводника. 3.Плотность заряда(заряд на ед. площади) =0. 4. Потенциал точек равен внутри и на поверхности проводника.

Вопрос 59 Ток смещения

Явление электромагнитной индукции свидетельствует, что переменное магнитное поле порождает в пространстве вихревое электрическое поле . Гениальная догадка Максвелла, позволившая ему построить замкнутую систему уравнений, описывающих все макроскопические электрические и магнитные явления, заключалась в предположении, что переменное электрическое поле порождает магнитное поле аналогично электрическому току. Новое понятие, позволяющее количественно описать это явление – ток смещения. К понятию тока смещения можно подойти путем следующих рассуждений. При зарядке конденсатора, по проводам, соединяющим конденсатор с источником тока, в течение короткого промежутка времени течет ток, сила которого зависит от времени. Этот ток порождает в пространстве переменное магнитное поле. Попытаемся выяснить, останется ли формула,записанная в виде )где – плотность тока, (справедливая в случае постоянных токов и полей) справедливой и при наличии в пространстве изменяющихся полей и токов. Пусть плоский контур L охватывает проводник (провод, соединенный с одной из обкладок конденсатора) с током I (рис. 1.28). Выбирая в качестве поверхности, натянутой на контур, поверхность S ₁ , пересекающую проводник, получим .(1.98) В то же время для поверхности S ₂ ,опирающейся на контур L и не пересекающей проводник, а охватывающей обкладку конденсатора, будем иметь(1.99) поскольку в любой точке этой поверхности. Отсюда следует, что при наличии изменяющихся токов соотношение (1.97) не может быть верным и его необходимо видоизменить. В случае конденсатора легко связать силу тока проводимости в проводнике со скоростью изменения электрического смещения между обкладками. Действительно, сила тока равна скорости изменения заряда на обкладках: . (1.100) Однако q = s S₀ , где S₀ – площадь обкладки; s – поверхностная плотность заряда на ней. Величина электрического смещения между обкладками D = s , поэтому .(1.101) Мы перешли к частной производной по времени по той причине, что в общем случае электрическое смещение различно в разных точках пространства. Введем понятие плотности тока смещения .(1.102) С учетом (1.101) имеем, (1.103) где – часть поверхности S ₂ , лежащая между обкладками. Поскольку вне обкладок , интегрирование можно распространить на всю поверхность S ₂ : .(1.104) Таким образом, если видоизменить соотношение (1.97) следующим образом: ,(1.105) оно оказывается справедливым и для поверхности S ₁ , натянутой на контур L , и для поверхности S ₂ . Анализируя различные конкретные ситуации, в которых поля и токи являются переменными, Максвелл пришел к выводу, что соотношение (1.105) является универсальным.

Величина (1.106) называется плотностью полного тока .

Билет 8 Вопрос 18

Электрический ток – упорядоченное движение эл.зарядов. Направление тока принято считать движение положительных зарядов.Характеристика поля: сила тока (I=dq\dtколич-во зарядов за 1 времени) и плотность тока(j=dI\dS –сила тока проходящая за 1 поперечного сечения проводника).\ j=const, I=const – ток постоянный. Стороние силы – силы источника тока.

Вопрос 47 Проинтегрировав выражение A=IФ^/ определим работу, совершаемую силами Ампера, при конечном произвольном перемещении контура в магнитном поле: A=IФ Т.е. работа по перемещению замкнутого контура с током в магнитном поле равна произведению силы тока в контуре на изменение магнитного потока, сцепленного с контуром.

Билет 9 Вопрос 5 Связь между потенциалом и напряженностью электрического поля .

Связьвыразим через элементарную работу dA. Так dA = qEcosbdl, где b - угол между Е и dl. С другой стороны, выразим через потенциал, работа dA = qdj . Из этих выражений следует, чтоdj =Ecosbdl = = E_l dl, и j = . Обратная связь между напряженностью и приращением потенциала , напряженность поля – вектор. Поэтому производная должна иметь смысл производной по направлению . Для положительногоПоэтому перед производной необходимо поставить знак минус, т.е. . Из этого выражения видно, что величина производной зависит от угла между Е и dl. Так для направления, перпендикулярного Е , проекция E_l равна нулю; наоборот, для направле-ния вдоль Е производная по dl максимальна и равна Е, т.е.

_{в направлении Е} . Термин «производная по направлению» становится более понятным в применении к прямо-угольным координатам. Рассматривая поочередно проекции Е на оси x,y и z можно напи-сать: где i,j, и k- единичные вектора вдоль осей x, y и z соответственно. Сам вектор Е нахо-дится как сумма:

E = Е_х + Е_у + Е_z . В теории поля производная по направлению наибольшего изменения функции называется градиентом (grad ), т.е. связь между напряженностью и потенциалом имеет вид:

E = - grad j

Вопрос 7 4

Блок схема радиоприемника, работающего на оговоренном принципе, показана на рис. 2.39. Радиоприемник, работающий по такой схеме, называется радиоприемником прямого усиления.

Радиоприемник прямого усиления обладает тем

.

Супергетеродинный приемник по сравнению с приемником прямого усиления имеет следующие преимущества: высокую чувствительность, что обеспечивается, прежде всего, большим усилением сигнала на промежуточной частоте, на которой паразитные емкости играют гораздо меньшую роль, чем на высоких частотах; высокую избирательность, благодаря применению неперестраиваемых резонансных контуров.

низкой частоты и подавая его на телефон, получим колебания мембраны телефона, воспроизводящие передаваемый Достигая антенны радиоприемника, волны возбуждают в ней очень слабые токи, тождественные токам в антенне радиопередатчика. Эти колебания выделяются в колебательном контуре, настроенном в резонанс с частотой принимаемого высокочастотного сигнала, и усиливаются с помощью усилителя высокой частоты. Однако, если эти колебания передать непосредственно на телефон, мы не сможем услышать звук, поскольку, во первых, мембрана телефона вследствие своей инерционности не сможет колебаться с частотой ~ 10⁵ – 10⁸ Гц, а во вторых звуковые колебания таких частот не улавливаются человечески ухом. Поэтому усиление колебания высокой частоты подвергают детектированию (демодуляции), получая колебания звуковой частоты. Схема простейшего демодулятора изображена на рис. 4.37. В этой схемеД – полупроводниковый диод, называемый в такой схеме детектором. Если на вход демодулятора подать модулированное напряжение u_вх , то на резисторе R , благодаря односторонней проводимости детектораД , при отсутствии конденсатора С получим пульсирующее напряжение (рис. 4.38,b). Если время разрядки конденсатора превосходит период высокочастотных несущих колебаний, пульсации напряжения сглаживаются, поэтому колебания напряжения на сопротивлении R будут воспроизводить модулирующие колебания низкой частоты (см. рис. 4.38,с). Усиливая это напряжение с помощью усилителя звук.

Блок схема радиоприемника, работающего на оговоренном принципе показана на рис. 4.39. Радиоприемник, работающий по такой схеме называется радиоприемником прямого усиления.

Радиоприемник прямого усиления обладает тем недостатком, что при высоких частотах в таком приемнике сильно сказываются паразитные емкости (емкости соединительных проводов, электродов ламп усилителя и т.д.),которые не позволяют получить хорошего усиления сигнала. Поэтому в настоящее время наибольшее распространение получил так называемый супергетеродинный приемник, блок-схема которого изображена на рис. 4.40.

В супергетеродинном радиоприемнике модулированные колебания высокой частоты w , улавливаемые антенной подаются на смеситель, на который одновременно подаются и колебания с гетеродина частоты w ₁ . Гетеродин является маломощным генератором и служит для генерации колебаний вспомогательной частоты, которая, как правило, выбирается выше частоты принимаемого сигнала. В смесителе колебания принятого сигнала и сигнала с гетеродина складываются (смешиваются), и в результате на его выходе получаются колебания промежуточной частоты w _пр = w ₁ – w . Эти колебания поступают на усилитель напряжения промежуточной частоты, где обеспечивается усиление сигнала до величины необходимой для нормальной работы демодулятора. Далее колебания звуковой частоты усиливаются и подаются на телефон.

Супергетеродинный приемник по сравнению с приемником прямого усиления имеет следующие преимущества: высокую чувствительность, благодаря прежде всего, большому усилению на промежуточной частоте, на которой паразитные емкости играют гораздо меньшую роль, чем на высоких частотах; высокую избирательность, благодаря применению большого числа неперестраиваемых резонансных контуров.

Билет 10 Вопрос 52

Явление и закон электромагнитной индукции.

Закон Ленца:в замкнутом проводящем контуре при изменении магнитного потока, пронизывающего этот контур, возникает электрический ток

Причина изменения магнитного потока может быть любой. Получить индукционный ток можно, например, следующим образом. Расположим рядом две катушки, одна из которых замкнута через гальванометр, а другая подсоединяется к источнику тока (рис. 1.23). При замыкании ключа K стрелка гальванометра отклоняется, показывая кратковременное появление тока. Возникновение индукционного тока можно вызвать перемещением этих катушек друг относительно друга (при замкнутом ключе К ), либо просто вдвигая в катушку постоянный магнит.

Явление электромагнитной индукции показывает, что можно не только получить магнитное поле с помощью тока, но и получить электрический ток при помощи магнитного поля. Этим была установлена глубокая связь между электрическими и магнитными явлениями.

Возникновение индукционного тока свидетельствует о том, что при изменении магнитного потока в контуре возникает электродвижущая сила . Основной закон электромагнитной индукции гласит: величина ЭДС индукции пропорциональна скорости изменения магнитного потока через площадь, ограниченную контуром :

.(1.71)

В СИ коэффициент пропорциональности равен единице и величина ЭДС индукции равна

. (1.72)

Электродвижущая сила в цепи возникает только тогда, когда на заряды в этой цепи действуют сторонние силы, силы неэлектростатического происхождения . Максвелл :причина появления ЭДС индукции – возникновение электрического поля, под действием которого электроны проводимости приходят в движение, вызывая ток в замкнутом контуре. Проводник при этом служит лишь прибором, позволяющим обнаружить это поле.

В отличие от электростатического поля, порождаемого неподвижными зарядами, это поле имеет замкнутые силовые линии, т.е. является вихревым полем. Оно вызывает в замкнутом проводнике движение электронов вдоль него и приводит к возникновению ЭДС.

правило Ленца гласит: индукционный ток в контуре имеет всегда такое направление, что создаваемый им магнитный поток препятствует изменению магнитного потока, вызвавшего этот индукционный ток.

Знак потока вектора магнитной индукции зависит от выбора нормали к контуру. За положительное направление обхода контура принимается направление, связанное с направлениемнормали правилом буравчика

Рассмотрим в магнитном поле замкнутый проводящий контур (рис. 1.24). Пусть направление поля совпадает с направлением выбранной нормали. Если поле меняется таким образом, что поток через площадь контура увеличивается, то согласно правилу Ленца,направление индукционного тока будет противоположно указанному стрелкой положительному направлению обхода контура (ЭДС отрицательна). Если же поток уменьшается, то направление индукционного тока будет совпадать с направлением обхода (ЭДС положительна). С учетом этого, закон электромагнитной индукции принимает окончательный вид:

..

Вопрос 22

R=l/S-сопротивление Виды сопротивления:

-последовательное R=R₁ +R₂ +R_n

-параллельное 1/R=1/R₁ +_……. +1/R_N

В металлах свободными частицами(носителями тока) являются электроны, в жидкостях – ионы, в плазме – электроны и ионы.

Билет 11 Вопрос 24

Для расчета сложных электрических цепей немецким ученым Кирхгофом были сформулированы эмпирические правила. Первое из них утверждает, чтодля любого узла электрической цепи сумма токов, входящих и выходящих из него, равна нулю. При этом токам приписывается определенный знак: входящие и выходящие токи имеют различные знаки. Пример показан на рис.16.Второе правило касается замкнутого контура, выделенного в сложной цепи: сумма произведений токов на сопротивления, по которым они проходят, равняется сумме ЭДС, включенных в данный контур. При этом токам и ЭДС приписывается определенный знак: при заданном направлении обхода контура положительными берутся только те токи (и ЭДС), которые совпадают с выбранным направлением обхода контура. Изрис. следует: I₁ – I₂ + I₃ –I₄ = 0, I₁ R₁ + I₂ R₂ - I₄ R₄ + I₃ R₃ = E₃ – E₂ – E₁ .

Вопрос 55 Взаимная индукция. Взаимоиндуктивность.

Рассмотрим взаимное влияние двух близко расположенных контуров с током см. рис. Часть магнитного поля, порождаемого контуром 1, будет пронизывать контур 2. С другой стороны, часть магнитного поля, создаваемого током в контуре 2, будет пронизывать контур 1. В этом случае говорят, что между контурами существует магнитная связь. Магнитная индукция поля, создаваемого контуром 1, пропорциональна силе тока i ₁ в нем. Поэтому магнитный поток Ф ₁₂ через контур 2 будет пропорционален i ₁ : Ф ₁₂ = L ₁₂ i ₁ ,(1.84) где коэффициент L₁₂ называется коэффициентом взаимной индукции контуров 1 и 2. Он равен магнитному потоку, создаваемому контуром 1 и пронизывающему контур 2, при силе тока в контуре 1, равной 1 А . Аналогично, Ф ₂₁ = L ₂₁ i ₂ , (1.85) где Ф ₂₁ – поток через контур 1, создаваемый в нем контуром 2 при силе тока в нем i ₂ . Можно показать, что для любых двух контуров коэффициенты взаимной индукции всегда равны, если среда, в которой находятся контура, не является ферромагнитной: L ₁₂ = L ₂₁ . (1.86) Коэффициент взаимной индукции зависит от размеров и формы контуров, их взаимного расположения и магнитных свойств окружающей среды . При изменении силы тока i ₁ в контуре 2 возбуждается ЭДС (1.87) Аналогично при изменении i ₂ в первом контуре возникает ЭДС .

Скачать архив с текстом документа