Шпоры по эконометрике

СОДЕРЖАНИЕ: 1. СПЕЦИФИКАЦИЯ МОДЕЛИ Простая регрессия представляет собой регрессию между двумя переменными —у и х, т.е. модель вида , где — результативный признак;

Шпоры по эконометрике.

№ 1. СПЕЦИФИКАЦИЯ МОДЕЛИ

Простая регрессия представляет собой регрессию между двумя переменными —у и х, т.е. модель вида , где у — результативный признак; х - признак-фактор.

Множественная регрессия представляет собой регрессию результативного признака с двумя и большим числом факторов, т. е. модель вида

Специ­фикация модели - формулировка вида модели, исходя из со­ответствующей теории связи между переменными. В урав­нении регрессии корреляционная по сути связь признаков представляется в виде функциональной связи, выраженной соответствующей математической функцией. где y_j — фактическое значение результативного признака;

y_xj -теоретическое значение результативного признака.

— случайная величина, характеризующая отклонения реального значения результативного признака от теоретического.

Случайная величина называется также возмущением. Она включает влияние не учтенных в модели факторов, случайных ошибок и особенностей измерения.

От правильно выбранной спецификации модели за­висит величина случайных ошибок: они тем меньше, чем в боль­шей мере теоретические значения результативного признака подходят к фактическим данным у.

К ошибкам спецификации относятся непра­вильный выбор той или иной математической функции для, и недоучет в уравнении регрессии какого-либо существенного фактора, т. е. использование парной регрессии вместо множест­венной.

Ошиб­ки выборки - исследователь чаще всего имеет дело с выборочными данными при установлении закономерной связи между признаками.

Ошибки измерения практически сводят на нет все усилия по количественной оценке связи между признаками. Основное внимание в эконометрических исследованиях уделяется ошибкам спецификации модели.

В парной регрессии выбор вида математической функции может быть осуществлен тремя методами: графическим, аналитическим и экспериментальным.

Графи­ческий метод основан на поле корреляции. Аналитический метод основан на изучении материальной природы связи исследуемых признаков.

Экспериментальный метод осуществляется путем сравнения величины остаточной дисперсии D_ост , рассчитанной при разных моделях. Если фактические значения результативного признака совпадают с теоретическими у =, то D_ocm =0. Если имеют место отклонения фактических данных от теоретических (у — ) то .

Чем меньше величина остаточной дисперсии, тем лучше уравнение регрессии подходит к исходным данным. Число наблюдений должно в 6 — 7 раз превышать число рассчитывае­мых параметров при переменной х.

№ 2 ЛИНЕЙНАЯ РЕГРЕССИЯ И КОРРЕЛЯЦИЯ: СМЫСЛ И ОЦЕНКА ПАРАМЕТРОВ.

Линейная регрессия сводится к нахождению уравнения вида или .

Уравнение вида позволяет по заданным значениям фактора x иметь теоретические значения результативного признака, подставляя в него фактические значения фактора х.

Построение линейной регрессии сводится к оценке ее пара­метров а и в.

Оценки параметров линейной регрессии могут быть найдены разными методами.

1.

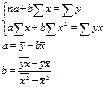
2.

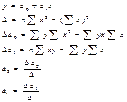
Параметр b называется коэффициентом регрессии. Его вели­чина показывает среднее изменение результата с изменением фактора на одну единицу.

Формально а — значение у при х = 0. Если признак-фактор
не имеет и не может иметь нулевого значения, то вышеуказанная
трактовка свободного члена, а не имеет смысла. Параметр, а может
не иметь экономического содержания. Попытки экономически
интерпретировать параметр, а могут привести к абсурду, особенно при а 0.

Интерпретировать можно лишь знак при параметре а. Если а 0, то относительное изменение результата происходит медленнее, чем изменение фактора.

Уравнение регрессии всегда дополняется показателем тесноты связи. При использовании линейной регрессии в качестве такого показателя выступает линейный коэффициент корреляции r_xy . Существуют разные модификации формулы линейного коэф­фициента корреляции.

Линейный коэффициент корреляции находится и границах: -1. r_xy 1. При этом чем ближе r к 0 тем слабее корреляция и наоборот чем ближе r к 1 или -1, тем сильнее корреляция, т.е. зависимость х и у близка к линейной. Если r в точности =1или -1 все точки лежат на одной прямой. Если коэф. регрессии b0 то 0 .r_xy 1 и наоборот при b0 -1.r_xy 0. Коэф. корреляции отражает степени линейной зависимости м/у величинами при наличии ярко выраженной зависимости др. вида.

Для оценки качества подбора линейной функции рассчитывается квадрат линейного коэффициента корреляции , называемый коэффициентом детерминации. Коэффициент детермина­ции характеризует долю дисперсии результативного признака y, объясняемую регрессией. Соответствующая величина характеризует долю дисперсии у, вызванную влиянием остальных не учтенных в модели факторов.

№ 3. МНК.

МНК позволяет получить такие оценки параметров а и b , которых сумма квадратов отклонений фактических значений ре­зультативного признака (у) от расчетных (теоретических) ми­нимальна:

Иными словами, из всего множества линий линия регрессии на графике выбирается так, чтобы сумма квадратов расстояний по вертикали между точками и этой линией была бы минималь­ной. Решается система нормальных уравнений

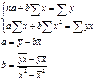
№ 4. ОЦЕНКА СУЩЕСТВЕННОСТИ ПАРАМЕТРОВ ЛИНЕЙНОЙ РЕГРЕССИИ И КОРРЕЛЯЦИИ .

Оценка значимости уравнения регрессии в целом дается с по­мощью F-критерия Фишера. При этом выдвигается нулевая ги­потеза, что коэффициент регрессии равен нулю, т. е. b = 0, и следовательно, фактор х не оказывает влияния на результат у.

Непосредственному расчету F-критерия предшествует анализ дисперсии. Центральное место в нем занимает разложе­ние общей суммы квадратов отклонений переменной у от средне го значения у на две части - «объясненную» и «необъясненную»:

- общая сумма квадратов отклонений

- сумма квадратов отклонения объясненная регрессией - остаточная сумма квадратов отклонения.

Любая сумма квадратов отклонений связана с числом степе­ней свободы, т. е. с числом свободы независимого варьирования признака. Число степеней свободы связано с числом единиц совокупности nис числом определяемых по ней констант. Применительно к исследуемой проблеме число cтепеней свободы должно показать, сколько независимых откло­нений из п возможных требуется для образования данной суммы квадратов.

Дисперсия на одну степень свободы D .

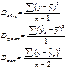
F-отношения (F-критерий):

Ecли нулевая гипотеза справедлива, то факторная и остаточная дисперсии не отличаются друг от друга. Для Н₀ необходимо опровержение, чтобы факторная дисперсия превышала остаточную в несколько раз. Английским статистиком Снедекором раз­работаны таблицы критических значений F-отношений при разных уровнях существенности нулевой гипотезы и различном числе степеней свободы. Табличное значение F-критерия — это максимальная величина отношения дисперсий, которая может иметь место при случайном их расхождении для данного уровня вероятности наличия нулевой гипотезы. Вычисленное значение F-отношения признается достоверным, если о больше табличного. В этом случае нулевая гипотеза об отсутствии связи признаков отклоняется и делается вывод о существенности этой связи: F_факт F_табл Н₀ отклоняется.

Если же величина окажется меньше табличной F_факт ‹, F_табл , то вероятность нулевой гипотезы выше заданного уровня и она не может быть отклонена без серьезного риска сделать неправильный вывод о наличии связи. В этом случае уравнение регрессии считается статистически незначимым. Н_о не отклоняется.

Стандартная ошибка коэффициента регрессии

Для оценки существенности коэффициента регрессии его ве­личина сравнивается с его стандартной ошибкой, т. е. определяется фактическое значение t-критерия Стьюдентa: которое

затем сравнивается с табличным значением при определенном уровне значимости и числе степеней свободы (n- 2).

Стандартная ошибка параметра а :

Значимость линейного коэффициента корреляции проверя­ется на основе величины ошибки коэффициента корреляции т _r :

Общая дисперсия признака х:

Коэф. регрессии Его величина показывает ср. изменение результата с изменением фактора на 1 ед.

Ошибка аппроксимации:

№ 5. ИНТЕРВАЛЫ ПРОГНОЗА ПО ЛИНЕЙНОМУ УРАВНЕНИЮ

РЕГРЕССИИ

Оценка стат. значимости параметров регрессии проводится с помощью t – статистики Стьюдента и путем расчета доверительного интервала для каждого из показателей. Выдвигается гипотеза Н₀ о статистически значимом отличие показателей от 0 a = b = r = 0. Рассчитываются стандартные ошибки параметров a,b, r и фактич. знач. t – критерия Стьюдента.

Определяется стат. значимость параметров.

t_a ›T_табл - a стат. значим

t_b ›T_табл - b стат. значим

Находятся границы доверительных интервалов.

Анализ верхней и нижней границ доверительных интервалов приводит к выводу о том, что параметры a и b находясь в указанных границах не принимают нулевых значений, т.е. не явл.. стат. незначимыми и существенно отличается от 0.

№ 6. НЕЛИНЕЙНАЯ РЕГРЕССИЯ. ВИДЫ МОДЕЛЕЙ

Если между экономическими явлениями существуют нели­нейные соотношения, то они выражаются с помощью соответ­ствующих нелинейных функций: например, равносторонней ги­перболы , параболы второй степени и д.р.

Различают два класса нелинейных регрессий:

• регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым па­раметрам;

• регрессии, нелинейные по оцениваемым параметрам.
Примером нелинейной регрессии по включаемым в нее объ­ясняющим переменным могут служить следующие функции:

• полиномы разных степеней

• равносторонняя гипербола

К нелинейным регрессиям по оцениваемым параметрам от­носятся функции:

• степенная

• показательная

• экспоненциальная

№ 7. СМЫСЛ КОЭФФИЦИЕНТА РЕГРЕССИИ.

Параметр b называется коэффициентом регрессии. Его вели­чина показывает среднее изменение результата с изменением фактора на одну единицу. Оценку коэффициента регрессии можно получить не обращаясь к методу наименьших квадратов. Альтернативную оценку параметра b можно найти исходя из содержания данного коэффициента: изменение результата сопоставляют с изменением фактора

Общая сумма квадратов отклонений индивидуальных значений результативного признака у от среднего значения вызвана влиянием множества причин. Условно разделим всю совокупность причин на две группы: изучаемый фактор х и прочие факторы.

Если фактор не оказывает влияния на результат, то линия регрес­сии на графике параллельна оси ох и .Тогда вся дисперсия результативного признака обусловлена воздействием прочих факторов и общая сумма квадратов отклонений совпадет с остаточной. Если же прочие факторы не влияют на результат, то у связан с х функционально и остаточная сумма квадратов равна нулю. В этом случае сумма квадратов отклонений, объясненная регрессией, совпадает с общей суммой квадратов.

Поскольку не все точки поля корреляции лежат на линии регрессии, то всегда имеет место их разброс как обусловленный вли­янием фактора х, т. е. регрессией у по х, так и вызванный действием прочих причин (необъясненная вариация). Пригод­ность линии регрессии для прогноза зависит от того, какая часть общей вариации признака у приходится на объясненную вариа­цию

Очевидно, что если сумма квадратов отклонений, обусловленная регрессией, будет больше остаточной суммы квадратов, то уравнение регрессии статистически значимо и фактор х оказывает существенное воздействие на результат у

Любая сумма квадратов отклонений связана с числом степе­ней свободы , т. е. с числом свободы независимого варьирования признака. Число степеней свободы связано с числом единиц совокупности n ис числом определяемых по ней констант. Применительно к исследуемой проблеме число степеней свободы должно показать, сколько независимых откло­нений из п возможных требуется для образования данной суммы квадратов.

№8. ПРИМЕНЕНИЕ МНК К МОДЕЛЯМ НЕЛИНЕЙНЫМ ОТНОСИТЕЛЬНО ВКЛЮЧАЕМЫХ ПЕРЕМЕННЫХ И ОЦЕНИВАЕМЫХ ПАРАМЕТРОВ.

Нелинейная регрессия по включенным переменным не таит каких-либо сложностей в оценке ее параметров. Она определяет­ся, как и в линейной регрессии, методом наименьших квадратов (МНК), ибо эти функции линейны по параметрам. Так, в парабо­ле второй степени y=a₀ +a₁ x+a₂ x² + заменяя переменные x=x₁ ,x² =x₂ , получим двухфакторное урав­нение линейной регрессии: у=а₀ +а₁ х₁ +а₂ х₂ +

Парабола второй степени целесообразна к применению, если для определенного интервала значений фактора меняется харак­тер связи рассматриваемых признаков: прямая связь меняется на обратную или обратная на прямую. В этом случае определяется значение фактора, при котором достигается максимальное (или минимальное), значение результативного признака: приравнива­ем к нулю первую производную параболы второй степени: , т.е. b+2cx=0 и x=-b/2c

Применение МНК для оценки параметров параболы второй степени приводит к следующей системе нормальных уравнений:

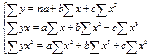Решение ее возможно методом определителей:

В моделях, нелинейных по оцениваемым параметрам, но приводимых к линейному виду, МНК применяется к преобразо­ванным уравнениям. Если в линейной модели и моделях, нели­нейных по переменным, при оценке параметров исходят из кри­терия min, то в моделях, нелинейных по оцениваемым параметрам, требование МНК применяется не к исходным дан­ным результативного признака, а к их преобразованным величи­нам, т. е.ln y, 1/y. Так, в степенной функции МНК применяется к преобразованному уравнению lny = ln + ln x ln . Это значит, что оценка параметров основывается на миними­зации суммы квадратов отклонений в логарифмах. Соответственно если в линейных моделях то в моделях, нелинейных по оцениваемым параметрам, . Вследствие этого оценка параметров оказываются несколько смещенной.

№9. КОЭФФИЦИЕНТЫ ЭЛАСТИЧНОСТИ ПО РАЗНЫМ ВИДАМ РЕГРЕССИОННЫХ МОДЕЛЕЙ.

1. Линейная y = a + bx + , y = b, Э = .

2. Парабола 2 порядка y = a +bx + c +, y = b + 2cx, Э = .

3. Гипербола y = a+b/x +, y=-b/, Э = .

4. Показательная y=a, y = ln , Э = x ln b.

5. Степенная y = a, y = , Э = b.

6. Полулогарифмическая y = a + b ln x + , y = b/x , Э = .

7. Логистическая , y = , Э = .

8. Обратная y = , y = , Э = .

№ 10 ПОКАЗАТЕЛИ КОРРЕЛЯЦИИ

1. индекс корреляции ( R ):

Величина данного показателя находится в границах: 0 R 1, чем ближе к 1, тем теснее связь рассматриваемых призна­ков, тем более надежно найденное уравнение регрессии.

2. индекс детерминации используется для проверки существенности в целом ур-ия нелинейной регрессии по F- критерию Фишера:

, где R² - индекс детерминации, n- число наблюдений, m – число параметров при переменной х.

№11. МНОЖЕСТВЕННАЯ РЕГРЕССИЯ. СПЕЦИФИКАЦИЯ МОДЕЛИ. ОТБОР ФАКТОРОВ ПРИ ПОСТРОЕНИИИ МОДЕЛИ.

Регрессия может дать хороший результат при модели­ровании, если влиянием других факторов, воздействующих на объект исследования, можно пренебречь. Поведение отдельных экономи­ческих переменных контролировать нельзя, т. е. не удается обес­печить равенство всех прочих условий для оценки влияния одно­го исследуемого фактора. В этом случае следует попытаться выявить влияние других факторов, введя их в модель, т. е. пост­роить уравнение множественной регрессии: y = a + b ₁ x ₁ + b ₂ +…+ b_p x_p + e ; Такого рода уравнение может использоваться при изучении потребления. Тогда коэффициенты bj — частные производные потребления у по соответствующим факторам x_i : , в предположении, что все остальные х_i постоянны. В 30-е гг. XX в. Кейнс сформулировал свою гипотезу потребительской функции. С того времени исследователи неод­нократно обращались к проблеме ее совершенствования. Совре­менная потребительская функция чаще всего рассматривается как модель вида: C = j ( y , P , M , Z ), где С — потребление; у — доход; Р — цена, индекс стоимости жизни; М — наличные деньги; Z — ликвидные активы. При этом .. Основная цель множественной регрессии — построить модель с большим числом факторов, определив при этом влияние каждого из них в отдельности, а также совокупное их воздействие на моделируемый показатель. Спецификация модели включает в себя два круга вопросов: отбор фак­торов и выбор вида уравнения регрессии. Требования к факторам.1 Они должны быть количественно измеримы. Если необхо­димо включить в модель качественный фактор, не имеющий ко­личественного измерения, то ему нужно придать количествен­ную определенность (например, в модели урожайности качество почвы задается в виде баллов) 2.Факторы не должны быть интеркоррелированы и тем более находиться в точной функциональной связи. Включение в модель факторов с высокой интеркорреляцией, когда R_{yx 1} R_{x 1 x 2} .Для зависимости y = a + b ₁ x ₁ + b ₂ +…+ b_p x_p + e может привести к нежелательным последствиям, повлечь за собой неустойчивость и ненадежность оценок коэффициентов регрессии. Если между факторами существует высокая корреляция, то нельзя определить их изолированное влияние на результативный показатель и параметры уравнения регрессии оказываются не интерпретированными.

Включаемые во множественную регрессию факторы должны объяснить вариацию независимой переменной. Если строится модель с набором р- факторов, то для нее рассчитывается показа­тель детерминации R ² , который фиксирует долю объясненной ва­риации результативного признака за счет рассматриваемых в ре­грессии р- факторов. Влияние других не учтенных в модели фак­торов оценивается как 1 - R ² с соответствующей остаточной дис­персией S² . При дополнительном включении в регрессию (р + 1) фактора коэффициент детерминации должен возрастать, а остаточная дисперсия уменьшаться:. Насыщение модели лишними факторами не только не снижа­ет величину остаточной дисперсии и не увеличивает показатель детерминации, но и приводит к статистической незначимости параметров регрессии по t-критерию Стьюдента.

Таким образом, хотя теоретически регрессионная модель позволяет учесть любое число факторов, практически в этом нет необходимости. Отбор факторов производится на основе качест­венного теоретико-экономического анализа, который обычно осуществляется в две стадии: на первой подби­раются факторы исходя из сущности проблемы; на второй – на основе показателей корреляции определяют t-статистики для параметров регрессии. Коэффициенты интеркорреляции (т. е. корреляции между объясняющими переменными) позволяют исключать из модели дублирующие факторы. Считается, что две переменных явно кол линеарны, т. е. находятся между собой в линейной зависимости, если . Ес­ли факторы явно коллинеарны, то они дублируют друг друга и один из них рекомендуется исключить из регрессии. Предпочте­ние при этом отдается не фактору, более тесно связанному с результатом, а тому фактору, который при достаточно тесной связи с результатом имеет наименьшую тесноту связи с другими факторами. В этом требовании проявляется специфика множест­венной регрессии как метода исследования комплексного воз­действия факторов в условиях их независимости друг от друга. Наибольшие труд­ности в использовании аппарата множественной регрессии воз­никают при наличии мультиколлинеарности факторов, когда более чем два фактора связаны между собой линейной зависимос­тью. Наличие мультиколлинеарности факторов может озна­чать, что некоторые факторы будут всегда действовать в унисон. В результате вариация в исходных данных перестает быть полно­стью независимой, и нельзя оценить воздействие каждого факто­ра в отдельности. Чем сильнее мультиколлинеарность факторов, тем менее надежна оценка распределения суммы объясненной вариации по отдельным факторам с помощью метода наименьших квадратов (МНК). Включение в модель мультиколлинеарных факторов нежела­тельно в силу следующих последствий: 1.затрудняется интерпретация параметров множественной ре­грессии как характеристик действия факторов в «чистом» ви­де, ибо факторы коррелированы; параметры линейной регрессии теряют экономический смысл;2оценки параметров ненадежны, обнаруживают большие стан­дартные ошибки и меняются с изменением объема наблюде­ний. Для оценки мультиколлинеарности факторов может исполь­зоваться определитель матрицы парных коэффициентов корреля­ ции между факторами.

Если бы факторы не коррелировали между собой, то матрица парных коэффициентов корреляции между факторами была бы единичной матрицей. Для включающего три объ­ясняющих переменных уравнения: y = a + b ₁ x ₁ + b ₂ + b ₃ x ₃ + e . Матрица коэф-в корреляции м/у факторами имела бы определитель равный 1. Det =1, т.к. r_{x 1 x 1} =r_{x 2 x 2} =1 и r_{x 1 x 2} =r_{x 1 x 3} =r_{x 2 x 3} =0. Если м/у факторами сущ-ет полная линейная зависимость и все коэф-ты корреляции =1, то определитель такой матрицы =0. Чем ближе к нулю определитель матрицы межфакторной корреляции, тем сильнее мультиколлинеарность факторов и ненадежнее результаты множественной регрессии. И, наоборот, чем ближе к единице определитель матрицы межфакторной кор­реляции, тем меньше мультиколлинеарность факторов.

№12. ЧТО ОЗНОЧАЕТ ВЗАИМОДЕЙСТВИЕ ФАКТОРОВ И КАК ОНО МОЖЕТ БЫТЬ ПРЕДСТАВЛЕНО ГРАФИЧЕСКИ?

Одним из путей учета внутренней корреляции факторов является переход к совмещенным уравнениям регрессии, т. е. к уравнениям, которые отражают не только влияние факторов, но и их взаимодействие. Так, если y=f(x1,x2,x3), то возможно пост­роение следующего совмещенного уравнения: y = a + b ₁ x ₁ + b ₂ x ₂ + b ₃ x ₃ + b ₁₂ x ₁ x ₂ + b ₁₃ x ₁ x ₃ + b ₂₃ x ₂ x ₃ + e . Рассматриваемое уравнение включает взаимодействие перво­го порядка (взаимодействие двух факторов). Возможно включе­ние в модель и взаимодействий более высокого порядка, если будет доказана их статистическая значимость по F-критерию Фи­шера. Если анализ совмещенного уравнения показал значи­мость только взаимодействия факторов х₁ и х₃ ,то уравнение бу­дет иметь вид: y = a + b ₁ x ₁ + b ₂ x ₂ + b ₃ x ₃ + b ₁₃ x ₁ x ₃ + e . Взаимодействие факторов х₁ и х₃ означает, что на разных уровнях фактора х₃ влияние фактора х₁ на у будет неодинаково, т. е. оно зависит от значений фактора х₃ . На рис. взаимодейст­вие факторов представляется непараллельными линиями связи с результатом у. И, наоборот, параллельные линии влияния факто­ра x₁ на у при разных уровнях фактора х₃ означают отсутствие вза­имодействия факторов х₁ и х₃ . Графики:

а — х₁ влияет на у, причем это влияние одинаково как при х₃ =В₁ , так и при х₃ =В₂ (одинаковый наклон линий регрессии), что означает отсутствие взаи­модействия факторов х₁ и х₃ ; б — с ростом х₁ результативный признак y возрастает при х₃ = В₁ ; с ростом х₁ результативный признак у снижается при х₃ = В₂ .. Между х₁ и х₃ существу­ет взаимодей-вие. Совмещенные уравнения регрессии строятся, например, при исследовании эффекта влияния на урожайность разных видов удобрений.Решению проблемы устранения мультиколлинеарности фак­торов может помочь и переход к уравнениям приведенной фор­мы. С этой целью в уравнение регрессии производится подста­новка рассматриваемого фактора через выражение его из другого уравнения.

№13. ИНТЕРПРИТАЦИЯ КОЭФФИЦИЕНТОВ РЕГРЕССИИ ЛИНЕЙНОЙ МОДЕЛИ ПОТРЕБЛЕНИЯ. СМЫСЛ СУММЫ b_i В ПРОИЗВОДСТВЕННЫХ ФУНКЦИЯХ И ЗНАЧЕНИЕ СУММЫ b_i 1 . КОЭФФИЦИЕНТЫ, ИСПОЛЬЗУЕМЫЕ ДЛЯ ОЦЕНКИ СРАВНИТЕЛЬНОЙ СИЛЫ ВОЗДЕЙСТВИЯ ФАКТОРОВ НА РЕЗУЛЬТАТ.

Функция потребления: С=К*у+L, где С-потребление, у-доход, К и L-параметры функции.(у=С+I, I-размер инвистиций). Предположим, что функция потребления составила :С= 1,9 + 0,65 *у . Коэффициент регрессии характеризует склонность к потреблению. Он показывает, что из каждой тысячи дохода на потреб­ление расходуется в среднем 650 руб., а 350 руб. инвестируются. В производственных функциях:

где Р - количество продукта, изготавливаемого с помощью т производст­венных факторов (F₁ , F ₂ ,..., F_m ); b - параметр, являющийся эластичностью количества продукции по отношению к количеству соответствующих производственных факторов.

Экономический смысл имеют не только коэффициенты b каждого фактора, но и их сумма, т. е. сумма эластичностей: В= b ₁ + b ₂ +...+ Ь_т . Эта величина фиксирует обобщенную харак­теристику эластичности производства.

При практических расчетах не всегда .Она может быть как больше, так и меньше единицы. В этом случае величина В фиксирует приближенную оценку эластичности выпуска с рос­том каждого фактора производства на 1 % в условиях увеличива­ющейся (В 1) или уменьшающейся (В 1) отдачи на масштаб. Так, если Р = 2,4* F * F₂ ^0,7 * F₃ ^0,2 , то с ростом значений каж­дого фактора производства на 1 % выпуск продукции в целом возрастает приблизительно на 1,2 %.

№14. НАЗНАЧЕНИЕ ЧАСТНОЙ КОРРЕЛЯЦИИ ПРИ ПОСТРОЕНИИ МОДЕЛИ МНОЖЕСТВЕННОЙ РЕГРЕССИИ. Ранжирование факторов, участву­ющих во множественной линейной регрессии, может быть прове­дено через стандартизованные коэффициенты регрессии, с помо­щью частных коэффициентов корреляции — для линейных связей. При нелинейной взаимосвязи исследуемых признаков эту функцию выполняют частные индексы детерминации. Кроме того, частные показатели корреляции широко используются при решении проблемы отбора факторов: целесообразность включе­ния того или иного фактора в модель доказывается величиной показателя частной корреляции.

Частные коэффициенты (или индексы) корреляции характери­зуют тесноту связи между результатом и соответствующим фак­тором при устранении влияния других факторов, включенных в уравнение регрессии.

Показатели частной корреляции представляют собой отно­шение сокращения остаточной дисперсии за счет дополнитель­ного включения в анализ нового фактора к остаточной диспер­сии, имевшей место до введения его в модель.

Частные коэффициенты корреляции измеряющие влияние на у фактора х_i при неизменном уровне др. факторов можно определить по формуле:

;

При двух факторах и i=1 данная формула примет вид:

Частные коэффициенты корреляции изменяются в пределах от -1 до 1.

№15. ЧАСТНЫЙ F -КРИТЕРИЙ, ЕГО ОТЛИЧИЕ ОТ ПОСЛЕДОВАТЕЛЬНОГО F -КРИТЕРИЯ, СВЯЗЬ МЕЖДУ СОБОЙ t - КРИТЕРИЯ СТЬЮДЕНТА ДЛЯ ОЦЕНКИ ЗНАЧИМОСТИ b_i И ЧАСТНЫМ F -КРИТЕРИЕМ .

Ввиду корреляции м/у факторами значимость одного и того же фактора м/б различной в зависимости от последовательности его введения в модель. Мерой для оценки включения фактора в модель служит частый F-критерий, т.е. F_xi . В общем виде для фактора x_i частый F-критерий определяется как :

Если рас­сматривается уравнение y = a + b ₁ x ₁ + b ₂ + b ₃ x ₃ + e , то определяются последовательно F-критерий для уравнения с од­ним фактором х₁ , далее F-критерий для дополнительного включе­ния в модель фактора х₂ , т. е. для перехода от однофакторного уравнения регрессии к двухфакторному, и, наконец, F-критерий для дополнительного включения в модель фактора х₃ , т. е. дается оценка значимости фактора х₃ после включения в модель факто­ров x₁ их₂ . В этом случае F-критерий для дополнительного вклю­чения фактора х₂ после х₁ является последовательным в отличие от F-критерия для дополнительного включения в модель фактора х₃ , который является частным F-критерием, ибо оценивает значи­мость фактора в предположении, что он включен в модель по­следним. С t-критерием Стьюдента связан именно частный F-критерий. Последовательный F-критерий может интересовать исследователя на стадии формирования модели. Для уравнения y = a + b ₁ x ₁ + b ₂ + b ₃ x ₃ + e оценка значимости коэффициентов регрессии Ь₁ ,Ь_2, , b ₃ предпола­гает расчет трех межфакторных коэффициентов детерминации, а именно: ,, и можно убедиться, что существует связь между собой t- критерия Стьюдента для оценки значимости b_i и частным F-критерием:

На основе соотношения b_i и получим:

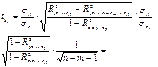
№16 ПРЕДПОСЫЛКИ МНК.

При оценке параметров уравнения регрессии применяется МНК. При этом делаются определенные предпосылки относительно составляющей , которая представляет собой ненаблюдаемую величину.

Исследования остатков - предполагают проверку наличия сле­дующих пяти предпосылок МНК: 1.случайный характер остатков; 2.нулевая средняя величина остатков, не зависящая от х_i ;

3.гомоскедастичность —дисперсия каждого отклонения ,одинакова для всех значений х; 4.отсутствие автокорреляции остатков. Значения остатков , распределены независимо друг от друга; 5.остатки подчиняются нормальному распределению.

1. Проверяется случайный характер остатков , с этой целью строится график зависимости остатков от теоретических значений результативного признака. Если на графике получена горизонтальная полоса, то остатки , представляют собой случайные величины и МНК оправдан, те­оретические значения у_х хорошо аппроксимируют фактические значения y. В других случаях необходимо либо применять дру­гую функцию, либо вводить дополнительную информацию и за­ново строить уравнение регрессии до тех пор, пока остатки , не будут случайными величинами.

2. Вторая предпосылка МНК относительно нулевой средней ве­личины остатков означает, что (у — у_х ) = 0. Это выполнимо для линейных моделей и моделей, нелинейных относительно вклю­чаемых переменных. С этой целью наряду с изложенным графиком зависимости остатков от теоретических значений ре­зультативного признака у_х строится график зависимости случай­ных остатков от факторов, включенных в регрессию х_{i .} Если остатки на графике расположены в виде горизонтальной полосы, то они независимы от значений x_j . Если же график показывает наличие зависимости и х_j то модель неадек­ватна. Причины неадекватности могут быть разные.

3. В соответствии с третьей предпосылкой МНК требуется, что­бы дисперсия остатков была гомоскедастичной. Это значит, что для каждого значения фактора x_j остатки , имеют одинаковую дисперсию. Если это условие применения МНК не соблюдается, то имеет место гетероскедастичность. Наличие гетероскедастичности можно наглядно видеть из поля корреляции. Гомоскедастичность остатков означает, что дисперсия остат­ков - одинакова для каждого значения х .

4.Отсутствие автокор­реляции остатков, т. е. значения остатков распределены неза­висимо друг от друга. Автокорреляция остатков означает наличие корреляции между остатками текущих и предыдущих (последующих) наблюдений. Отсутствие автокорреляции остаточных величин обеспечива­ет состоятельность и эффективность оценок коэффициентов ре­грессии.

№17. СУЩНОСТЬ АНАЛИЗА ОСТАТКОВ ПРИ НАЛИЧИИ РЕГРЕССИОННОЙ МОДЕЛИ. КАК МОЖНО ПРОВЕРИТЬ НАЛИЧИЕ ГОМО- ИЛИ ГЕТЕРОСКЕДАСТИЧНОСТИ ОСТАТКОВ. ОЦЕНКА ОТСУТСТВИЯ АВТОКОРРЕЛЯЦИИ ОСТАТКОВ ПРИ ПОСТРОЕНИИ СТАТИСТИЧЕСКОЙ РЕГРЕССИОННОЙ МОДЕЛИ.

С этой целью строиться график зависимости остатков e_i от теоретических значений результативного признака:

Если на графике получена горизонтальная полоса, то остатки e_i представляют собой случайные величины и МНК оправдан, те­оретические значения у_х хорошо аппроксимируют фактические значения у.

Возможны следующие случаи: если e_i зависит от у _x , то: 1.остатки e_i не случайны.2. остатки e_i , не имеют постоянной дисперсии. 3. Остатки e_i носят систематический характер в дан­ном случае отрицательные значения e_i , соответствуют низким значениям у_х , а положительные — высоким значениям. В этих случаях необходимо либо применять дру­гую функцию, либо вводить дополнительную информацию.

Как можно проверить наличие гомо- или гетероскедастичноси остатков? Гомоскедастичность остатков означает, что дисперсия остатков e_i одинакова для каждого значения х. Если это условие применения МНК не соблюдается, то имеет место гетероскедастичность. Наличие гетероскедастичности можно наглядно видеть из поля корреляции. а — дисперсия остатков растет по мере увеличения х; б — дисперсия остатков достигает максимальной величины при средних значениях переменной х и уменьшается при минимальных и максимальных значениях х; в — максимальная дисперсия остатков при

малых значениях х и дисперсия остатков однородна по мере увеличения значений х. Графики гомо- и гетеро-ти.

Оценка отсутствия автокорреляции остатков (т.е. значения остатков e_i распределены независимо друг от друга). Автокорреляция остатков означает наличие корреляции между остатками текущих и предыдущих (последующих) наблюдений. Коэффициент корреляции между e_i и e_j , где e_i — остатки текущих наблюдений, e_j — остатки предыдущих наблю­дений, может быть определен по обычной формуле линейного коэффициента корреляции . Если этот коэффициент окажется существенно отличным от ну­ля, то остатки автокоррелированы и функция плотности вероят­ности F(e ) зависит j-й точки наблюдения и от распределения значений остатков в других точках наблюдения. Для регрессионных моделей по статической информации ав­токорреляция остатков может быть подсчитана, если наблюдения упорядочены по фактору х . Отсутствие автокорреляции остаточных величин обеспечива­ет состоятельность и эффективность оценок коэффициентов ре­грессии. Особенно актуально соблюдение данной предпосылки МНК при построении регрессионных моделей по рядам динами­ки, где ввиду наличия тенденции последующие уровни динами­ческого ряда, как правило, зависят от своих предыдущих уров­ней.

№18 СМЫСЛ ОБОБЩЕННОГО МНК .

При нарушении гомоскедастичности и наличии автокорреля­ции ошибок рекомендуется традиционный МНК заменять обобщенным методом. Обобщенный МНК применяется к преобразованным данным и позволяет получать оценки, которые обладают не только свойством несмещенности, но и имеют меньшие выборочные дисперсии. Обобщенный МНК для корректировки гетерос-ти. В общем виде для уравнения y_i =a+bx_i +e _i при где K_i – коэф-т пропор-ти. Модель примет вид: y_i =+x_i +e _i . В ней остаточные величины гетероскедастичны. Предполагая в них отсутствие автокорреляции, можно перейти к уравнению с гомоскедастичными остатками, поделив все переменные, зафик­сированные в ходе i-го наблюдения на . Тогда дисперсия остатков будет величиной постоянной. От регрессии у по х мы перейдем к регрессии на новых переменных: y / и х/ . Уравнение регрессии примет вид: . По отношению к обычной регрессии уравнение с новыми, преобразованными переменными представляет собой взвешен­ную регрессию, в которой переменные у и х взяты с весами . Коэф-т регрессии b можно определить как Как видим, при использовании обобщенного МНК с целью корректировки гетероскедастичности коэффициент регрессии b представляет собой взвешенную величину по отношению к обычному МНК с весами 1/К.Аналогичный подход возможен не только для уравнения парной, но и для множественной регрессии. Модель примет вид: . Модель с преобразованными переменными составит

. Это уравнение не содер-т свобод-го члена, применяя обычный МНК получим: Применение в этом случае обобщенного МНК приводит к то­му, что наблюдения с меньшими значениями преобразованных переменных х/К имеют при определении параметров регрессии относительно больший вес, чем с первоначальными переменны­ми.

№19. СИСТЕМЫ ЭКОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ. ПРОБЛЕМА ИДЕНТИФИКАЦИИ.

Сложные экономические процессы описывают с помощью системы взаимосвязанных уравнений. Различают несколько видов систем уравнений: 1. Система независимых уравнений - когда каждая зависимая переменная у рассматривается как функция одного и того же набора факторов х :

y ₁ = a ₁₁ * x ₁ + a ₁₂ * x ₂ +…+ a _{1 m} * x_m + e ₁ Для решения этой системы и нахождения ее параметров

y_n =a_n1 *x₁ +a_n2 *x₂ +…+a_nm *x_m +e_n используется МНК.

2.Система рекурсивных уравнений – когда зависимая переменная у одного уравнения выступает в виде фактора х в другом уравнении:

y₁ =a₁₁ *x₁ +a₁₂ *x₂ +…+a_1m *x_m +e₁

y₂ =b₂₁ *y₁ +a₂₁ *x₁ +a₂₂ *x₂ +…+a_2m *x_m +e₂

y₃ =b₃₁ *y₁ +b₃₂ *y₂ +a₃₁ *x₁ +a₃₂ *x₂ +…+a_3m *x_m +e₃

y_n =b_n1 *y₁ +b_n2 *y₂ +…+b_nn-1 *y_n-1 +a_n1 *x₁ +a_n2 *x₂ +…+a_nm *x_m +e_n

Для решения этой системы и нахождения ее параметров используется МНК.

3 Система взаимосвязанных уравнений – когда одни и те же зависимые переменные в одних уравнениях входят в левую часть, а в других – в правую.

y₁₌ b₁₂ *y₂ +b₁₃ *y₃ +…+b_1n *y_n +a₁₁ *x₁ +a₁₂ *x₂ +…+a_1m *x_m +e₁

y₂ =b₂₁ *y₁ +b₂₃ *y₃ +…+b_2n *y_n +a₂₁ *x₁ +a₂₂ *x₂ +…+a_2m *x_m +e₂

y_n =b_n1 *y₁ +b_n2 *y₂ +…+b_nn-1 *y_n-1 +a_n1 *x₁ +a_n2 *x₂ +…+a_nm *x_m +e_n

Такая система уравнений называется структурной формой модели. Эндогенные переменные – взаимосвязанные переменные, которые определяются внутри модели (системы) у. Экзогенные переменные – независимые переменные, которые определяются вне системы х. Предопределенные переменные – экзогенные и лаговые (за предыдущие моменты времени) эндогенные переменные системы. Коэффициенты a и b при переменных – структурные коэффициенты модели. Система линейных функций эндогенных переменных от всех предопределенных переменных системы - приведенная форма модели.

где - коэффициенты приведенной формы модели.

Необходимое условие идентификации – выполнение счетного правила:

D+1=H –уравнение идентифицируемо;

D+1H – уравнение неидентифицируемо;

D+1H – уравнение сверхидентифицируемо.

Где Н – число эндогенных переменных в уравнении, D – число предопределенных переменных, отсутствующих в уравнении, но присутствующих в системе.

Достаточное условие идентификации- определитель матрицы, составленной из коэффициентов при переменных, отсутствующих в исследуемом уравнении на равен нулю и ранг этой матрицы не менее эндогенных переменных без единицы. Для решения идентифицируемого уравнения применяется КМНК, для решения сверхидентифицируемых - двухшаговый МНК.

№20 КМНК . Применяется в случае точно идентифицируемой модели. Процедура применения КМНК предполагает выполнение следующих этапов: 1. Составляют приведенную форму модели и определяют численные значения параметров для каждого ее уравнения обычным МНК. 2. путем алгебраических преобразований переходят от приведенной формы к уравнениям структурной формы модели, получая тем самым численные оценки структурных параметров.

№21 ДВУХШАГОВЫЙ МНК. (ДМНК)

Основная идея ДМНК — на основе приведенной формы модели получить для сверхидентифицируемого уравнения теоретические значения эндогенных переменных, содержащихся в правой части уравнения. Далее, подставив их вместо фактических значений, можно применить обычный МНК к структурной форме сверхидентифи­цируемого уравнения. Метод получил название двухшагового МНК, ибо дважды используется МНК: на первом шаге при определении приведенной формы модели и нахождении на ее основе оценок теоретических значений эндогенной переменной

и на втором шаге применительно к структурному сверхидентифицируемому уравнению при опре­делении структурных коэффициентов модели по данным теоре­тических (расчетных) значений эндогенных переменных.

Сверхидентифицируемая структурная модель может быть двух типов:

• все уравнения системы сверхидентифицируемы;

• система содержит наряду со сверхидентифицируемыми точно
идентифицируемые уравнения.

Если все уравнения системы сверхидентифицируемые, то для оценки структурных коэффициентов каждого уравнения исполь­зуется ДМНК. Если в системе есть точно идентифицируемые уравнения, то структурные коэффициенты по ним находятся из системы приведенных уравнений.

Применим ДМНК к простейшей сверхидентифицируемой

модели:

Данная модель может быть получена из предыдущей иденти­фицируемой модели:

если наложить ограничения на ее параметры, а именно: b₁₂ =a₁₁

В результате первое уравнение стало сверхидентифицируемым: Н= 1 (у₁ ),

D = 1(х₂ ) и D +1 Н. Второе уравнение не изме­нилось и является точно идентифицируемым: Н = 2 и D =1

На первом шаге найдем приведенную форму модели, а

именно:

ДМНК является наиболее общим и широко распространен­ным методом решения системы одновременных уравнений.

Несмотря на важность системы эконометрических уравнений, на практике часто не принимают во внимание некоторые взаимосвязи, применение традиционного МНК к одному или нескольким уравнениям также широко распространено в эконометрике. В частности, при построении производственных функций анализ спроса можно вести, используя обычный МНК.

№22 ОСНОВНЫЕ ЭЛЕМЕНТЫ ВРЕМЕННОГО РЯДА.

Временной ряд — это совокупность значений какого-либо по­казателя за несколько последовательных моментов или периодов времени. Каждый уровень временного ряда формируется под воздействием большого числа факторов, которые условно можно подразделить на три группы:

• факторы, формирующие тенденцию ряда;

• факторы, формирующие циклические колебания ряда;

• случайные факторы.

При различных сочетаниях в изучаемом явлении или процессе этих факторов зависимость уровней ряда от времени может принимать различные формы. Во-первых, большинство времен­ных рядов экономических показателей имеют тенденцию, харак­теризующую совокупное долговременное воздействие множества факторов на динамику изучаемого показателя. Очевидно, что эти факторы, взятые в отдельности, могут оказывать разнонаправ­ленное воздействие на исследуемый показатель. Однако в сово­купности они формируют его возрастающую или убывающую тенденцию. Рис1

Во-вторых, изучаемый показатель может быть подвержен циклическим колебаниям. Эти колебания могут носить сезон­ный характер, поскольку экономическая деятельность ряда от­раслей экономики зависит от времени года рис2 Некоторые временные ряды не содержат тенденции и цикли­ческой компоненты, а каждый следующий их уровень образуется как сумма среднего уровня ряда и некоторой (положительной или отрицательной) случайной компоненты. Рис3

В большинстве случаев фактический уровень временного ря­да можно представить как сумму или произведение трендовой, циклической и случайной компонент. Модель, в которой вре­менной ряд представлен как сумма перечисленных компонент, называется аддитивной моделью временного ряда. Модель, в ко­торой временной ряд представлен как произведение перечислен­ных компонент, называется мультипликативной моделью времен­ного ряда. Основная задача эконометрического исследования от дельного временного ряда — выявление и придание количествен­ного выражения каждой из перечисленных выше компонент с тем, чтобы использовать полученную информацию для прогно­зирования будущих значений ряда или при построении моделей взаимосвязи двух или более временных рядов.

№23. АВТОКОРРЕЛЯЦИЯ УРОВНЕЙ ВРЕМЕННОГО РЯДА

Корреляционную зависимость между последова­тельными уровнями временного ряда называют автокорреляцией уровней ряда. Количественно ее можно измерить с помощью линейного ко­эффициента корреляции между уровнями исходного временного ряда и уровнями этого ряда, сдвинутыми на несколько шагов во времени. Коэффициент корреляции имеет вид:

можно определить коэффициенты автокорреля­ции второго и более высоких порядков. Так, коэффициент авто­корреляции второго порядка характеризует тесноту связи между уровнями у _t и y_{t -1} и определяется по формуле:

Число периодов, по которым рассчитывается коэффициент автокорреляции, называют лагом. С увеличением лага число пар значений, по которым рассчитывается коэффициент автокорре­ляции, уменьшается.

Отметим два важных свойства коэффициента автокорреляции. Во-первых, он строится по аналогии с линейным коэффициентом корреляции и таким образом характеризует тесноту только линейной связи текущего и предыдущего уровней ряда.

Во-вторых, по знаку коэффициента автокорреляции нельзя делать вывод о возрастающей или убывающей тенденции в уров­нях ряда.

Последовательность коэффициентов автокорреляции уров­ней первого, второго и т. д. порядков называют автокорреляцион­ ной функцией временного ряда. График зависимости ее значений от величины лага на­зывается коррелограммой.

№24. МОДЕЛИРОВАНИЕ ТЕНДЕНЦИЙ ВРЕМЕННОГО РЯДА (АНАЛИТИЧЕСКОЕ ВЫРАВНИВАНИЕ ВРЕМЕННОГО РЯДА)

Одним из наиболее распространенных способов моделирова­ния тенденции временного ряда является построение аналитиче­ской функции, характеризующей зависимость уровней ряда от времени, или тренда. Этот способ называют аналитическим вы­ равниванием временного ряда.

Поскольку зависимость от времени может принимать разные формы, для ее формализации можно использовать различные ви­ды функций. Для построения трендов чаще всего применяются следующие функции:

• линейный тренд:

• гипербола: ,

• экспоненциальный тренд:

• тренд в форме степенной функции:

• парабола второго и более высоких порядков:

Параметры каждого из перечисленных выше трендов можно определить обычным МНК, используя в качестве независимой переменной время t=1,2,..., n, а в качестве зависимой перемен- 1 ной — фактические уровни временного ряда y_t . Существует несколько способов определения типа тенденции. К числу наиболее распространенных способов относятся качественный анализ изучаемого процесса, построение и визуальный анализ графика зависимости уровней ряда от времени, расчет некоторых основных показателей динамики. В этих же целях можно использовать и коэффициенты автокорреляции уровней ряда. Тип тенденции можно определить путем сравнения коэф­фициентов автокорреляции первого порядка, рассчитанных по исходным и преобразованным уровням ряда. Если временной ряд имеет линейную тенденцию, то его соседние уровни у _t и у _{t -1} тес­но коррелируют. В этом случае коэффициент автокорреляции первого порядка уровней исходного ряда должен быть высоким. Если временной ряд содержит нелинейную тенденцию, напри­мер, в форме экспоненты, то коэффициент автокорреляции пер­вого порядка по логарифмам уровней исходного ряда будет вы­ше, чем соответствующий коэффициент, рассчитанный по уров­ням ряда. Чем сильнее выражена нелинейная тенденция в изуча­емом временно м ряде, тем в большей степени будут различаться значения указанных коэффициентов.

Выбор наилучшего уравнения в случае, если ряд содержит не­линейную тенденцию, можно осуществить путем перебора ос­новных форм тренда, расчета по каждому уравнению скорректи­рованного коэффициента детерминации R ² и выбора уравнения тренда с максимальным значением скорректированного коэффи­циента детерминации.

№;25. ММЕТОДЫ ИСКЛЮЧЕНИЯ ТЕНДЕНЦИЙ. МЕТОД ОТКЛОНЕНИЙ ОТ ТРЕНДА.

Сущность всех методов исключения тенденции заключается в том, чтобы устранить или зафиксировать воздействие фактора времени на формирование уровней ряда. Основные методы исклю­ чения тенденции можно разделить на две группы:

• методы, основанные на преобразовании уровней исходного
ряда в новые переменные, не содержащие тенденции. Полу­ченные переменные используются далее для анализа взаимо­связи изучаемых временных рядов. Эти методы предполага­ют непосредственное устранение трендовой компоненты Т из каждого уровня временного ряда. Два основных метода в
данной группе — это метод последовательных разностей и
метод отклонений от трендов;

• методы, основанные на изучении взаимосвязи исходных
уровней временных рядов при элиминировании воздействия
фактора времени на зависимую и независимые переменные
модели. В первую очередь это метод включения в модель рег­рессии по временным рядам фактора времени.
Рассмотрим подробнее методику применения, преимущества и недостатки каждого из перечисленных выше методов. Метод отклонений от тренда

Пусть имеются два временных ряда x_t и y_t каждый из которых содержит трендовую компоненту Т и случайную компоненту е. Проведение аналитического выравнивания по каждому из этих рядов позволяет найти параметры соответствующих уравнений трендов и определить расчетные по тренду уровни соответственно. Эти расчетные значения можно принять за оценку трендовой компоненты Т каждого ряда. Поэтому влияние тенденции можно устранить путем вычитания расчетных значений уровней ряда из фактических. Эту процедуру проделывают для каждого временного ряда в модели. Дальнейший анализ взаимосвязи ря­дов проводят с использованием не исходных уровней, а отклонений от тренда и при условии, что последние не содержат тенденции.

№26. МЕТОД ПОСЛЕДОВАТЕЛЬНЫХ РАЗНОСТЕЙ .

В ряде случаев вместо аналитического выравнивания времен­ного ряда с целью устранения тенденции можно применить более простой метод — метод последовательных разностей.

Если временной ряд содержит ярко выраженную линейную тенденцию, ее можно устранить путем замены исходных уровней ряда цепными абсолютными приростами (первыми разностями).

Пусть (1) ;

Тогда (6.3) Тогда

Коэффициент b — константа, которая не зависит от времени.

Если временной ряд содержит тенденцию в форме параболы второго порядка, то для ее устранения можно заменить исходные уровни ряда на вторые разности.

Пусть имеет место соотношение (1), однако

Тогда

Как показывает это соотношение, первые разности _t , непо­средственно зависят от фактора времени t и, следовательно, со­держат тенденцию.

Определим вторые разности:

Очевидно, что вторые разности _t ² , не содержат тенденции, поэтому при наличии в исходных уровнях тренда в форме пара­болы второго порядка их можно использовать для дальнейшего анализа. Если тенденции временного ряда соответствует экспо­ненциальный или степенной тренд, метод последовательных раз­ностей следует применять не к исходным уровням ряда, а к их ло­гарифмам.

№27. ВКЛЮЧЕНИЕ В МОДЕЛЬ РЕГРЕССИИ ФАКТОРА ВРЕМЕНИ.

В корреляционно-регрессионном анализе устранить воздей­ствие какого-либо фактора можно, если зафиксировать воздейст­вие этого фактора на результат и другие включенные в модель факторы. Этот прием широко используется в анализе временных рядов, когда тенденция фиксируется через включение фактора времени в модель в качестве независимой переменной.

Модель вида относится к группе моделей, включающих фактор времени. Оче­видно, что число независимых переменных в такой модели может быть больше единицы. Кроме того, это могут быть не только те­кущие, но и лаговые значения независимой переменной, а также лаговые значения результативной переменной. Преимущество данной модели по сравнению с методами от­клонений от трендов и последовательных разностей в том, что она позволяет учесть всю информацию, содержащуюся в исход­ных данных, поскольку значения y_t и х _t есть уровни исходных временных рядов. Кроме того, модель строится по всей совокуп­ности данных за рассматриваемый период в отличие от метода последовательных разностей, который приводит к потере числа наблюдений. Параметры а и b модели с включением фактора вре­мени определяются обычным МНК.

Система нормальных уравнений имеет вид:

№28 .АВТОКОРРЕЛЯЦИЯ В ОСТАТКАХ. КРИТЕРИЙ ДАРБИНА-УОТСОНА.

Существуют два наиболее распространенных метода опреде­ления автокорреляции остатков. Первый метод — это построение графика зависимости остатков от времени и визуальное определение наличия или отсутствия автокорреляции. Второй метод — использо­ вание критерия Дарбина — Уотсона и расчет величины

(1)

Таким образом, d есть отношение суммы квадратов разностей последовательных значений остатков к остаточной сумме квадра­тов по модели регрессии. Можно предположить что: , предположим также

Коэффициент автокорреляции остатков оп­ределяется как

С учетом (3) имеем:

Таким образом, если в остатках существует полная положи­тельная автокорреляция и , то d = 0. Если в остатках полная отрицательная автокорреляция, то и, следовательно, d = 4.Если автокорреляция остатков отсутствует, то и d = 2. Следовательно, 0d4

Алгоритм выявления автокорреляции остатков на основе критерия Дарбина — Уотсона следующий. Выдвигается гипотеза Н₀ об отсутствии автокорреляции остатков. Альтернативные ги­потезы Н₁ Н₁ * состоят, соответственно, в наличии положитель­ной или отрицательной автокорреляции в остатках. Далее по спе­циальным таблицам определяются критичес­кие значения критерия Дарбина — Уотсона d_l и d_u для заданного числа наблюдений n, числа независимых переменных модели к и уровня значимости . По этим значениям числовой промежуток [0;4] разбивают на пять отрезков. Если фактическое значение критерия Дарбина — Уотсона по­падает в зону неопределенности, то на практике предполагают существование автокорреляции остатков и отклоняют гипотезу H_о .

№29 . ОБЩАЯ ХАРАКТЕРИСТИКА МОДЕЛЕЙ С РАСПРЕДЕЛЕННЫМ ЛАГОМ. ИНТЕРПРИТАЦИЯ ПАРАМЕТРОВ МОДЕЛЕЙ С РАСПРЕДЕЛЕННЫМ ЛАГОМ .

Величину L, характеризующую запаздывание в воздействии фактора на результат, называют в эконометрике лагом, а временные ряды самих факторных переменных, сдвинутые на один ил более моментов времени, — лаговыми переменными.

Эконометрическое моделирование осуществляется с применением моделей, содержащих не только текущие, но и лаговые значения факторных переменных. Эти модели называются моделями с распределенным лагом. Модель вида

является примером модели с распределенным лагом.

Наряду с лаговыми значениями независимых, или факторных, переменных на величину зависимой переменной текущего периода могут оказывать влияние ее значения в прошлые моменты или периоды времени. Эти процессы обычно описывают с помощью моделей регрессии, содержащих в качестве факторов лаговые значения зависимой переменной, которые называются моделями авторегрессии. Модель вида

относится к моделям авторегрессии. Построение моделей с распределенным лагом и моделей ав­торегрессии имеет свою специфику. Во-первых, оценка парамет­ров моделей авторегрессии, а в большинстве случаев и моделей с распределенным лагом не может быть произведена с помощью обычного МНК ввиду нарушения его предпосылок и требует спе­циальных статистических методов. Во-вторых, исследователям приходится решать проблемы выбора оптимальной величины лага и определения его структуры. Наконец, в-третьих, между моделями с распределенным лагом и моделями авторегрессии су­ществует определенная взаимосвязь, и в некоторых случаях необ­ходимо осуществлять переход от одного типа моделей к другому. Интерпретация параметров моделей с распределительным лагом. Рассмотрим модель с распределенным лагом в ее общем виде в предположении, что максимальная величина лага конечна:

Эта модель говорит о том, что если в некоторый момент вре­мени t происходит изменение независимой переменной х, то это изменение будет влиять на значения переменной у в течение l следующих моментов времени.

Коэффициент регрессии b₀ при переменной x_t характеризует среднее абсолютное изменение у _t при изменении х _t на 1 ед. свое­го измерения в некоторый фиксированный момент времени t , без учета воздействия лаговых значений фактора x. Этот коэффици­ент называют краткосрочным мультипликатором.

В момент (t+1) совокупное воздействие факторной перемен­ной x_t на результат у_t , составит (b₀ + b₁ ) усл. ед., в момент (t+2) это воздействие можно охарактеризовать суммой ( b ₀ + b ₁ + b ₂ ) и т. д. Полученные таким образом суммы называют промежуточными мультипликаторами.

Введем следующее обозначение:

b₀ +b₁ +…+b_l =b

Величину b называют долгосрочным мультипликатором. Он по­казывает абсолютное изменение в долгосрочном периоде t + l ре­зультата у под влиянием изменения на 1 ед. фактора х.

Предположим

_j =b_j /b, j=0:1

Назовем полученные величины относительными коэффициен­ тами модели с распределенным лагом. Сред­ ний лаг определяется по формуле средней арифметической взве­шенной: и представляет собой средний период, в течение которого будет происходить изменение результата под воздействием изменения фактора в момент времени t . Небольшая величина среднего лага свидетельствует об относительно быстром реагировании резуль­тата на изменение фактора, тогда как высокое его значение гово­рит о том, что воздействие фактора на результат будет сказывать­ся в течение длительного периода времени. Медианный лаг — это величина лага, для которого

Это тот период времени, в течение которого с момента време­ни t будет реализована половина общего воздействия фактора на результат.

№ 30 МЕТОД АЛМОНА.

В методе А. предполагается ,что веса текущих лаговых значений объясняющих переменных подчиняются палениальному распределению. b_j = c₀ +c₁ j+ c₂ j² +…+ c_k j^k

Уравнение регрессии примет вид y_t = a+c₀ z₀ +c₁ z₁ + c₂ z₂ + c_k z_k +_t , где z_i =; i=1,…,k; j=1,…,p. Расчет параметров модели с распределенным лагом проводится по следующей схеме:

1. Устанавливается макси. величина лага l.

2. Определяется степень паленома k,описывающего структуру лага.

3. Рассчитывается значение переменных с z₀ до z_{k .}

4. Определяются параметры уравнения линейной регрессии y_t (z_i ).

5. Рассчитываются параметры исходной модели с распределенным лагом.

№ 31 МЕТОД КОЙКА.

В распределение Койка делается предположение, что коэффициенты при лаговых значениях объясняющей переменной убывают в геометрической прогрессии. b_l =b₀ ^l ; l=0,1,2,3; 0 1. Уравнение регрессии преобразовывается к виду:

y_t =a+b₀ x_t +b₀ x_{t -1} +b₀ ² x_{t -2} +…+ _t . После несложных преобразований получаем ур-ие оценки параметров исходящего ур-ия.

№ 32 МЕТОД ГЛАВНЫХ КОМПОНЕНТ.

Суть метода — сократить число объясняющих пе­ременных до наиболее существенно влияющих факторов. Метод главных компонент применяется для исключе­ния или уменьшения мультиколлинеарности объясняющих пере­менных регрессии. Основная идея заключается в сокращении числа объясняющих переменных до наиболее существенно влия­ющих факторов. Это достигается путем линейного преобразова­ния всех объясняющих переменных xⁱ (i=0,..,n) в новые пере­менные, так называемые главные компоненты. При этом требу­ется, чтобы выделению первой главной компоненты соответство­вал максимум общей дисперсии всех объясняющих переменных xⁱ (i=0,..,n). Второй компоненте — максимум оставшейся дис­персии, после того как влияние первой главной компоненты ис­ключается и т. д.

№ 33 МОДЕЛИ АВТОРЕГРЕССИИ. ОЦЕНКА ПАРАМЕТРОВ МОДЕЛЕЙ АВТОРЕГРЕССИИ.

Модели содержащие в качестве факторов лаговые знач. зависимой переменной называются моделями авторегрессии. Н-р y_t =a+b₀ x_t +c₁ y_{t -1} + _{t .} Как и в модели с распределенным лагом b₀ и в этой модели характеризует краткосрочные изменения y_t под воздействием изменения х₁ на 1 ед. Долгосрочный мультипликатор в модели авторегрессии рассчитывается как сумма краткосрочного и промежуточных мультипликаторов b = b₀ +b₀ c₁ +b₀ c₁ ² +b₀ c₁ ³ +…=b₀ (1+c₁ +c₁ ² +c₁ ³ +…)=b₀ /1-c₁

Отметим, что такая интерпретация коэффициентов модели авторегрессии и расчет долгосрочного мультипликатора основаны на предпосылке о наличие бесконечного лага в воздействии текущего знач. зависимой переменной на ее будущее знач.

Одним из возможных методов расчета параметров уравнения авторегрессии является метод инструментальных переменных. Сущность этого метода состоит в том, чтобы заменить перемен­ную из правой части модели, для которой нарушаются предпо­сылки МНК, на новую переменную, включение которой в модель регрессии не приводит к нарушению его предпосылок. Примени­тельно к моделям авторегрессии необходимо удалить из правой части модели переменную y_{t -1} . Искомая новая переменная, кото­рая будет введена в модель вместо y_{t -1ь} должна иметь два свойст­ва. Во-первых, она должна тесно коррелировать с y_{t -1ь} во-вторых, она не должна коррелировать с остатками u_r .

Еще один метод, который можно применять для оценки пара­метров моделей авторегрессии типа — это метод максималь­ного правдоподобия

№34 ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ. ????????????????????

№ 35 МЕТОД ПОДВИЖНОГО (СКОЛЬЗЯЩЕГО) СРЕДНЕГО.

Метод простого скользящего ср. состоит в том, что расчет показателя на прогнозируемый момент времени строится путем усреднения значения этого показателя за несколько предшествующих моментов времени.

где х_{k - i} – реальное знач. показателя в момент времени t_{n -1.}

n- число предшествующих моментов времени использующих при расчете.

f_k – прогноз на момент времени t_{k .}

№ 36 МЕТОД ЭКСПОНЕНЦИАЛЬНОГО СГЛАЖИВАНИЯ.

Учитываются отклонения предыдущего прогноза от реального показателя а сам расчет проводится по след. формуле:

где x_{k -1} – реальное значение показателя в момент времени t_{k -1} .

f_k – прогноз на момент времени t_k .

– постоянное сглаживание.

Замечание: знач. подчиняется условию 0‹ ‹ 1, определяет степень сглаживания и обычно выбирается универсальным методом проб и ошибок.

№ 37 МЕТОД ПРОЕЦИРОВАНИЯ ТРЕНДА.

Основной идеей метода проецирования линейного тренда является построение прямой, которая в среднем наименее уклоняется от массива точек заданного временным рядом. Прямая ищется в виде: x = at + b (a и b -постоянные). Величины a и b удовлетворяют. следующей линейной системе:

№38. КАЗУАЛЬНЫЕ МЕТОДЫ ПРОГНОЗИРОВАНИЯ. КАЧЕСТВЕННЫЕ МЕТОДЫ ПРОГНОЗИРОВАНИЯ. ????????????????

Скачать архив с текстом документа