Синтез и анализ механизма двигателя внутреннего сгорания
СОДЕРЖАНИЕ: Содержание Введение 1 Постановка задач проекта 2 Синтез кинематической схемы механизма 3 Синтез рычажного механизма 4 Синтез кулачкового механизмаСодержание
Введение
1 Постановка задач проекта
2 Синтез кинематической схемы механизма
3 Синтез рычажного механизма
4 Синтез кулачкового механизма
5 Синтез зубчатого механизма
6 Кинематический анализ механизма
7 Динамический анализ механизма
8 Оптимизация параметров механизма
Заключение
Список использованных источников
Введение
На современном этапе развития науки и техники большая роль отводится машиностроению, в рамках которого изучаются общие методы исследования свойств механизмов и проектирования их схем независимо от конкретного назначения машины. Это необходимо для того, чтобы повысить надежность машин и оборудования. Данная проблема рассматривается в курсе теории механизмов и машин.
Изучение дисциплины «Теория механизмов и машин» проводится с широким применением ЭВМ, а также математического и программного обеспечения.
Задачи теории механизмов и машин разнообразны. Важнейшие из них это:
- анализ механизмов;
- синтез механизмов;
- теория машин-автоматов.
Анализ механизма состоит в исследовании кинематических и динамических свойств механизма по заданной схеме.
Синтез механизма состоит в проектировании схемы механизма по заданным его свойствам.
Разделение теории механизмов на анализ и синтез носит условный характер, так как часто схему механизма и его параметры определяют путем сравнительного анализа различных механизмов, воспроизводящих одни и те же движения. Этот сравнительный анализ возможных вариантов механизма составляет теперь основу методов синтеза с использованием ЭВМ. Также в процессе синтеза механизма приходится выполнять проверочные расчеты, используя методы анализа.
Значение курса теории механизмов и машин для подготовки инженеров, проектирующих новые машины и механизмы, очевидно, так как общие методы синтеза механизмов, излагаемые в этом курсе, дают возможность находить параметры механизмов с заданными кинематическими и динамическими свойствами.
1 Постановка задач проекта
Задачи курсового проекта:
-освоение методов синтеза механизмов и определение их основных параметров;
-освоение методов кинематического и динамического анализа синтезированного механизма;
-приобретение навыков оптимизации параметров механизма методом перебора.
Исходные данные:
Тип двигателя –V-образный.
Кривошипно – шатунный механизм:
H= 12010-3 м – ход поршня;
D= 12010-3 м – диаметр поршня;
l= 0.35 – отношение длины кривошипа к длине шатуна;
mп = 3.5кг – масса поршня;
mш =9кг – масса шатуна;
w1 = 250 рад/с – угловая скорость кривошипа;
max = 300 – максимальный угол давления.
Кулачковый механизм:
h= 1010-3 м – высота подъема толкателя;
jy = 840 – угол удаления;
тип толкателя – плоский;
закон движения – синусоидальный.
Зубчатый механизм:
u=8 – передаточное число механизма.
Требуется:
-синтезировать кривошипно-шатунный, кулачковый и зубчатый механизмы;
-произвести динамический анализ кривошипно - шатунного механизма;
-определить оптимальные параметры механизма, чтобы обеспечивался заданный закон изменения скорости поршня.
2 Синтез кинематической схемы механизма
Кинематическая схема механизма включает основные подсистемы автомобиля: кривошипно-шатунный и газораспределительный механизмы.
Кривошипно-шатунный механизм включает кривошип, шатун, поршень.
Схема кривошипно – шатунного механизма представлена на рисунке 2.1.
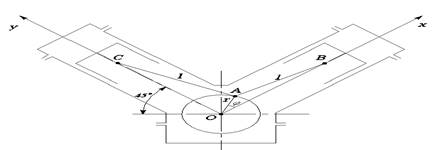
Рисунок 2.1 - Схема кривошипно – шатунного механизма
Газораспределительный механизм включает в себя кулачок и плоский толкатель.
Схема газораспределительного механизма представлена на рисунке 2.2.
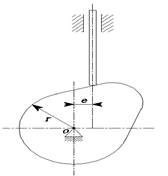
Рисунок 2.2 - Схема газораспределительного механизма
3 Синтез рычажного механизма
Синтез рычажного механизма предусматривает определение основных параметров кривошипно-шатунного механизма – длины кривошипа, хода поршня, а также определение зависимости перемещения, скорости и ускорения поршня от угла поворота коленчатого вала.
Для определения основных параметров кривошипно-шатунного механизма рассмотрим рисунок 3.1.
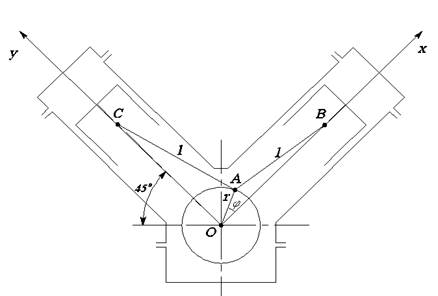
Рисунок 3.1 - Схема кривошипно – шатунного механизма V – образного двигателя с углом развала 900
Оси координат удобнее всего направить вдоль цилиндров, а для упрощения расчетов по определению параметров КШМ отбросим второй цилиндр и дальнейшие рассуждения, будем вести относительно одного цилиндра (рисунок 3.2) .
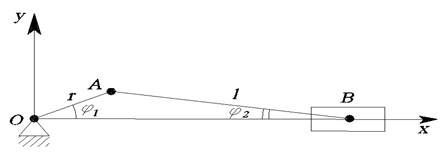
Рисунок 3.2 - Схема одного цилиндра КШМ
Определим неизвестные параметры r и l КШМ, используя формулы:
r=0.5H (3.1)
l=r/ (3.2)
где r - длина кривошипа;
l - длина шатуна.
Численные значения параметров r и l определим, записав формулы 3.1 и 3.2 в программе MathCAD. Получаем:
r = 0.03 м;
l = 0.171 м.
Необходимое условие проворачиваемости звеньев выполняется при угле давления max равным 30 градусам.
Параметры кривошипно – шатунного механизма заносим в таблицу 3.1.
Таблица 3.1 - параметры кривошипно-шатунного механизма
| Параметр |
Значение |
Размерность |
| H |
12010-3 |
м |
| D |
12010-3 |
м |
| r |
3010-3 |
м |
| l |
17110-3 |
м |
| 0.35 |
- |
|
| max |
30 |
град. |
4 Синтез кулачкового механизма
Основными геометрическими параметрами кулачкового механизма с поступательно движущимся толкателем являются радиус кулачка и эксцентриситет.
Определение радиуса кулачка, а также дальнейшие вычисления будем производить, используя программу MаthCAD.
Определим радиус кулачка по формуле (4.1):
r0 =la(1 )-S(1 )l (4.1)
где a(1 ) – минимальное значение функции ускорения толкателя по углу поворота кулачка 1 ;
S(1 ) – значение перемещения толкателя при угле поворота кулачка 1 .
Значение эксцентриситета, в случае с плоским толкателем, не влияет на определение профиля кулачка, поэтому его находить не будем.
В механизме с плоским толкателем координаты конца радиус - вектора r1 определяются по формулам:
xА =V(j) (4.2)
yА =r0 + S(j) (4.3)
где V(j) – значение скорости толкателя при угле поворота 1 .
Величину радиус – вектора r1 определим по формуле:
r1 (j1 )=(xА (j)2 + уА (j)2 )1/2 (4.5)
С учетом формул 4.2 и 4.3 получаем выражение для радиус – вектора r1
r1 (j) (V(j)2 + (r0 + S(j))2 )1/2 (4.6)
Для определения координат профиля кулачка необходимо спроецировать радиус - вектор на оси координат при повороте его на угл равный 360 градусов. Следовательно координаты профиля кулачка xК и уК будут равны:
xК (j)=r1 (j)cos(j) (4.7)
yК (j)=r1 j) cos(j) (4.8)
Построение профиля кулачка будем проводить в среде MathCAD. Для написания программы по построению профиля сначала введем переменные, которые заданы по условию:
h = 1010-3 м
jу = 840
Для построения графиков зависимостей ускорения, скорости и перемещения толкателя от угла поворота кулачка зададим угол j и его шаг:
j =0,/100..2
Далее с помощью программы опишем закон изменения ускорения толкателя от угла поворота j:
a(j)= (h2/jу 2 )sin(2j/ jу ) if j jу
- (h2/jу 2 )sin(2j/ jу ) if jу j2 jу
0 otherwise
Для определения значения угла 1 , в котором значение функции ускорения минимальное воспользуемся функцией Minimise, начальное значение угла 1 примем равное нулю:
1 = 0 1 = Minimise(а, 1 )
Функцию скорости толкателя от угла поворота j V(j) найдем с помощью интегрирования функции ускорения a(j). Затем проинтегрировав функцию скорости найдем функцию перемещения S(j). Интегрирование проводим в пределах от 0 до 2jу . Для этого cоставляем программы:
V(j)= a(j)dj if j 2jу
0 otherwise
![]() S(j)= V(j)dj if j 2jу
S(j)= V(j)dj if j 2jу
0 otherwise
Определив значения угла 1 , а также функции скорости и перемещения толкателя и последовательно подставляя эти значения в выражения 4.1, 4.2, 4.3, 4.6 ,4.7 и 4.8 получаем координаты профиля кулачка.
Профиль кулачка найдем, построив график функции Pr(j) от угла j :
Pr(j) = (xК (j)2 + yК (j)2 )1/2
Все вычисления и графики приведены в приложении А.
5 Синтез зубчатого механизма
Зубчатый механизм включает в себя планетарную и вальную передачи. Синтез зубчатого механизма заключается в определении чисел зубьев всех колес и передаточного числа планетарного механизма.
Схема зубчатого редуктора представлена на рисунке 5.1.
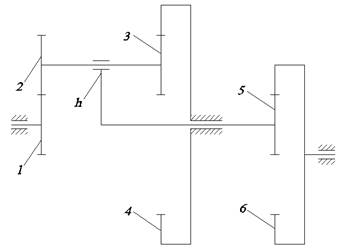
Рисунок 5.1 – Схема зубчатого механизма
По условию задано передаточное число всего механизма, равное произведению передаточного числа планетарной и вальной передачи:
U = Uпм Uвп U = 8
Выразим передаточное число всего механизма через числа зубьев с применением формулы Виллиса:
U= 1 – ( – z2 /z1 )(z4 /z3 ))z6 /z5 (5.1)
Примем передаточное число планетарного механизма равным Uпм = 4, а вальной передачи Uвп = 2. Тогда:
1–(z2 /z1 )(z4 /z3 ) = 4 (5.2)
где (z2 /z1 )(z4 /z3 ) = р – передаточное число механизма при остановленном водиле h.
Выбираем числа зубьев z4 и z3 равными соответственно 51 и 17. Используя условие соосности: z4 – z3 = z2 + z1 ; и выражение 5.2 найдем оставшиеся z2 и z1 . Решив систему с двумя неизвестными получаем : z1 = 17 ,
z2 = 17
Для определения числа зубьев колес вальной передачи примем z5 = 17 и определим число зубьев шестого колеса по выражению 5.1. Решив уравнение получаем z6 = 34.
Проверим правильность подбора зубьев по условиям соосности и сборки.
Условие соосности:
z4 – z3 = z2 + z1
51 – 17 = 17+17 = 34
Следовательно, условие соосности выполняется.
Условие сборки:
(z4 z2 +z3 z1 ) / kc = n
где kc = 2 – число саттелитов;
n – любое целое число.
(5117 + 1717)/1 = 1156
Условие сборки выполняется.
В результате проверки по условиям соосности и сборки видно, что числа зубьев подобраны верно.
Определим параметры эвольвентного зацепления зубчатых колес 1 и 2.
Рассчитаем параметры зацепления для колёс с модулями m=3, для зацепления с нулевым смещением.
Результаты занесем в таблицу.
Таблица 5.1 – Параметры зубчатого зацепления
| № колеса |
di , мм |
dbi, мм |
dai, мм |
dfi, мм |
Si, мм |
ai,град. |
xi, мм |
| 1 |
51 |
47.924 |
57 |
43.5 |
4.712 |
20 |
0 |
| 2 |
51 |
47.924 |
57 |
43.5 |
4.712 |
20 |
0 |
где di – диаметр делительной окружности;
dbi – диаметр основной окружности;
dai –диаметр окружности вершин;
dfi – диаметр окружности впадин;
Si – толщина зуба по делительной окружности;
ai – угол зацепления;
xi – смещение.
По данным параметрам строим зубчатое зацепление.
Все вычисления и эвольвентное зацепление представлены в приложении Б.
6 Кинематический анализ механизма
Для выполнения кинематического анализа необходимо решить его основные задачи: определение зависимости положений, линейных и угловых скоростей и ускорений звеньев от обобщенной координаты, в качестве которой выбираем угол поворота коленчатого вала.
Кинематический анализ рычажного механизма заключается в определении кинематических параметров поршня и шатуна, то есть их линейных и угловых перемещений, скоростей и ускорений.
Кинематический анализ кривошипно-шатунного механизма заключается в определении линейных перемещений, скорости и ускорения поршня. Перемещение поршня Sb в зависимости от угла поворота кривошипа 1 для механизма, изображенного на рисунке 3.2, описывается формулой:
Sb (1 ) = rcos(1 ) + lcos(2 )
где 2 (1 ) = arccos(1 – (r/l)sin(1 )2 )1/2 – угол поворота шатуна.
Определим зависимость скорости поршня от угла поворота коленчатого вала. График зависимости скорости поршня от угла поворота кривошипа 1 Vb (j1 ) получим дифференцированием функции перемещения поршня Sb (1 ):
Vb (j1 ) = (d Sb (1 )/d 1 )1
График зависимости ускорения поршня от угла поворота кривошипа 1 ab (j1 ) получим дифференцированием полученной функции скорости Vb(j1 ):
ab (j1 ) = (d V(j1 )/d 1 )1
Полученные зависимости перемещения,скорости и ускорения поршня от угла поворота кривошипа 1 и их вычисления представлены в приложении В.
7 Динамический анализ механизма
Задачей динамического анализа механизма является определение нагруженности в звеньях механизма и передаваемых моментов в процессе его функционирования.
В данной работе динамическая модель представляет собой простейшую математическую модель с одной степенью свободы. Составляем динамическую модель кривошипно-шатунного механизма. Для определения Мд используем формулу:
Мд 1 = Мi i + Pi Vi cos(Pi ^Vi )
где Мi – момент, приложенный к i – му звену;
Pi – сила, приложенная к i – му звену;
Vi – скорость i – го звена;
i – угловая скорость i – го звена.
Тогда выражение для момента, действующего от одного поршня, можно записать в следующем виде:
М(1 ) = P1 (1 )V1 (1 )/1
Затем разложим момент, действующий от одного поршня, на две составляющие: момент движущих сил и момент сил сопротивления. Момент движущих сил определим на промежутках от 00 до 1800 градусов и от 3600 до 4050 градусов, а момент сил сопротивления на промежутках от 1800 до 3600 и от 4050 до 7200 градусов .
Для этого запишем программы:
Mд (1 ) = M(1 ) if (01 ) and (21 9/4)
0 otherwise
Mc (1 ) = 0.7M(1 ) if (1 2) and (9/41 4)
1000 otherwise
Момент сил сопротивления определяем с учетом потерь на трение внутри цилиндра.
Далее определим угловое ускорение кривошипа:
1 (1 ) = (Mд (1 ) – Mc (1 ))/(J1 (1 )+Jм )
где J1 (1 ) – приведенный момент инерции;
Jм – момент инерции маховика.
Приведенный момент инерции вычисляется по формуле:
J1 (1 ) = (1/ 1 2 )( 2 2 (1 )J2 + mш Vs 2 (1 ) + mп V1 2 (1 ))
где 2 (1 ) – угловая скорость шатуна;
J2 – момент инерции шатуна равный mш l2 /12;
Vs (1 ) – скорость центра масс шатуна.
Определяем угловую скорость по формуле:
(1 ) = 1 + 1 (1 )d1
Характеристикой неравномерности установившегося движения является коэффициент неравномерности движения механизма:
= (imax – imin )/i ср
где imax – максимальная угловая скорость i – го звена приведения;
imin – минимальная угловая скорость i – го звена приведения;
i ср – средняя угловая скорость i – го звена приведения.
Допустимую величину коэффициента неравномерности dдоп для автомобильных двигателей примем 0.085.
Среднюю угловую скорость определим по формуле:
ср = (max + min )/2
Для этого в программе MаthCAD используем функцию Minner.
После определения характеристики неравномерности подбираем момент инерции маховика таким образом, чтобы выполнялось неравенство dдоп .
Вычисления и графики представлены в приложении В.
8 Оптимизация параметров механизма
Параметрическая оптимизация механизма заключается в поиске оптимальной совокупности значений его внутренних параметров с учетом технических требований. Поиск оптимальных параметров может осуществляться методами оптимизации либо методом перебора. Для этого критерии оптимальности выражают целевыми функциями, в основе которых лежат математические модели механизмов, представленные таким образом, что при оптимальной совокупности внутренних параметров механизмов, соответствующей наилучшему значению выходных параметров, целевые функции имеют экстремальное значение. В качестве целевой функции выступает зависимость, отражающая полноту удовлетворения предъявляемых к механизму требований.
В качестве критериев оптимальности наиболее часто используют отклонение между желаемыми кинематическими или динамическими характеристиками выходного звена и реально реализуемыми механизмом, точность воспроизведения заданной функции или траектории, максимальное ускорение выходного звена, к.п.д. и производительность механизма и т.д.
В качестве параметров оптимизации, т.е. параметров, варьируя которыми стремятся к минимизации целевой функции, выступают геометрические размеры механизма: длины звеньев, углы, расстояния между стойками и т.д.
В кривошипно–шатунном механизме в качестве критериев оптимальности выберем длину кривошипа r и длину шатуна l. Оптимизацию будем выполнять методом перебора: оставляя постоянным значение длины шатуна l, варьируем значением длины кривошипа r и находим значение целевой функции F для каждого значения r, затем, фиксируя оптимальное значение r, перебираем значение l, и также находим значение целевой функции F. Выражение для целевой функции получим определив среднее отклонение закона изменения скорости поршня от требуемого закона движения. Требуемый закон изменения скорости:
Vт (1 ) = –14sin(1 )+1.5
Тогда значение целевой функции равно:
F = V1 (1 ) – Vт (1 )
Среднее отклонение закона изменения скорости поршня от требуемого закона движения найдем непосредственно в программе с использованием функции mean.
Далее составляем программы для определения отклонения в зависимости от длины кривошипа r и шатуна l. Длину кривошипа r выберем, изменяющуюся в пределах от 0.03 до 0.082, а длину шатуна l от 0.082 до 0.171.
В качестве ограничения максимального угла давления max используем следующее выражение: sin(max ) = r/l.
Затем строим графики зависимости отклонений законов изменения скоростей поршня от требуемого закона движения от длины кривошипа r и шатуна l.
Для получения оптимальных значений длины шатуна l и кривошипа r составляем программы в среде MathCAD.
Вычисления, программы и графики представлены в приложении Г.
Заключение
Выполняя курсовой проект, были проведены следующие работы: синтез и анализ механизма двигателя внутреннего сгорания, оптимизация кривошипно – шатунного механизма, определены основные параметры зубчатого механизма и построено эвольвентное зубчатое зацепление.
В результате синтеза и анализа механизма двигателя внутреннего сгорания были определены основные параметры механизмов и получены законы их изменения.
При оптимизации кривошипно – шатунного механизма получены значения оптимальной длины кривошипа 0.03 и оптимальной длины шатуна 0.0171.
Для зубчатого механизма получены значения чисел зубьев колес: z1 =17; z2 =17;z3 =17;z4 =51;z5 =17;z6 =34.
Список использованных источников
К.И. Заблонский и др. Теория механизмов и машин. Учебник. — Киев: Вища школа. 1989. — 376 с.
И.М. Белоконев. Теория механизмов и машин. Методы автоматизированного проектирования. — Киев: Вища школа. — 1990. — 208 с.
Теория механизмов и механика машин / Под ред. К.В. Фролова: М., Высшая шк. — 1998. — 496с.
С.А. Попов, Г.А. Тимофеев. Курсовое проектирование по теории механизмов и машин. — М.: Высш. шк. — 1998. — 351 с.
Курсовое проектирование по теории механизмов и машин: Учеб. пос. / Под ред. А.С. Кореняко. — Киев: Вища школа. — 1970. — 332 с.
Л.С. Тетерюкова, В.Л. Комар. Кинематический расчет рычажных механизмов на ЭВМ методом замкнутых векторных контуров. Методические указания к курсовому проекту по теории механизмов и машин для всех специальностей. — Могилев: МГТУ, 2000. — 38 с.
Тарасик В.П., Бедункевич В.М. Функциональное проектирование планетарных коробок передач: Методические указания для курсового и дипломного проектирования. — Могилев: ММИ, 1996. — 30 с.