Синтез каскадной системы управления с дополнительным стабилизирующим регулятором

СОДЕРЖАНИЕ: Тема: Синтез каскадной системы управления с дополнительным стабилизирующим регулятором

Министерство образования

Российской Федерации

Санкт-Петербургский государственный горный институт им. Г.В. Плеханова

(технический университет)

КУРСОВАЯ РАБОТА

По дисциплине: Теория автоматического управления

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

Тема: Синтез каскадной системы управления с дополнительным стабилизирующим регулятором

Автор: студент гр. ЭР-98-2 _____________ / Кривецкий М. И. /

^{(подпись)} (Ф.И.О.)

ОЦЕНКА: _____________

Дата: ___________________

ПРОВЕРИЛ

Руководитель проекта: доцент ______________ / Стороженко С. В. /

^{(подпись) (Ф.И.О.)}

Санкт-Петербург

2001

Аннотация.

Данная курсовая работа содержит вариант расчёта каскадной САУ (выбор передаточной функции объекта управления, выбор параметров настроек регулятора и расчёт НЦУ). Пояснительная записка выполнена в программном приложении Microsoft Word. К работе прилагаются все необходимые графики.

The summary.

The given course activity contains version of calculation of a combined ACS (selection of a transfer function of object of control, selection of parameters of adjustments of the regulator and calculation DNC). The explanatory slip is executed in the programmatic appendix Microsoft Word. To activity all indispensable schedules are appended.

Содержание

Содержание.. 2

Введение. 3

1. Построение кривой переходного процесса по регулирующему каналу. 4

2. Получение математической модели объекта управления в виде передаточных функций.. 5

3. Расчет параметров стабилизирующего регулятора частотным методом на ЭВМ. 9

4. Выбор ПИ-алгоритма управления и расчет параметров внешнего корректирующего регулятора W_р2 (p) (графоаналитическим методом Ротача). 13

5. Построение переходного процесса в системе по задающему и возмущающему воздействиям. 18

Показатели качества переходных процессов. 19

6. Переход к непосредственному цифровому управлению. 20

Заключение.. 26

Список используемой литературы... 27

Введение.

Промышленные объекты управления, как правило, представляют собой сложные агрегаты со многими входными и выходными величинами, характеризующими технологический процесс. Зависимости выходных величин от входных, как правило, нелинейные, и изменение одной из них приводит к изменению других. Таким образом, создаётся сложная система взаимозависимостей, которую трудно, а подчас и невозможно строго математически описать.

Задачу можно существенно упростить, если считать зависимости выходных величин от входных линейными или линеаризуемыми в окрестностях малых отклонений от статических, рабочих режимов объекта. Поскольку при устойчивой работе автоматической системы регулирования (АСР) отклонения параметров в системе малы, такая линеаризация почти всегда оказывается допустимой. Кроме того, сложные объекты часто можно разбить на отдельные «регулируемые участки» («каналы»), взаимным влиянием отдельных каналов друг на друга можно пренебречь и рассматривать их как самостоятельные.

1. Построение кривой переходного процесса по регулирующему каналу.

Выполнить синтез каскадной САУ (рис.1.1) техническим объектом, заданным экспериментальной переходной характеристикой по управляющему каналу, приведенной в таблице (1).

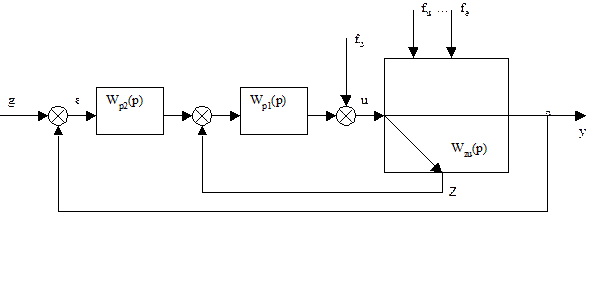
Рис. 1.1

Экспериментальная переходная характеристика.

Таблица 1.

t, c	Канал u-y
0	0
1	0
2	0,06
3	0,16
4	0,26
5	0,4
6	0,58
7	0,76
8	0,96
9	1.12
10	1.28
11	1.4
12	1.5
13	1.56
14	1.6
15	1.6

2. Получение математической модели объекта управления в виде передаточных функций

При разработке и исследовании автоматической системы управления получают ее математическое описание – описание процессов, проистекающих в системе, на языке математики. Математическое описание может быть аналитическим (с помощью уравнений), графическим (с помощью графиков и структурных схем) и табличным (с помощью таблиц).

Для получения математического описания системы обычно составляют описание ее отдельных элементов. В частности, для получения уравнений системы составляют уравнения для каждого входящего в нее элемента. Совокупность всех уравнений элементов и дает уравнения системы.

Уравнения (а так же структурные схемы) автоматической системы управления называют ее математической моделью. Такое название обусловлено тем, что при математическом описании (составлении уравнений) физических процессов всегда делают какие-либо допущения и приближения. Сказанное обуславливается тем, что к математической модели предъявляются противоречивые требования: она должна, с одной стороны как можно полнее отражать свойства оригинала, а с другой стороны, быть по возможности простой, чтобы не усложнять исследование.

Аппроксимируем переходную характеристику объекта по регулирующему каналу. Исследуемый объект по каналу регулирования является объектом с самовыравниванием (рис.1.1). Объекты с самовыравниванием аппроксимируют дробно-рациональными передаточными функциями с введением звена запаздывания:

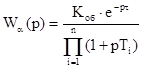, (2.1)

где К_об – коэффициент передачи; t - время запаздывания; Т_о – постоянная времени.

Первый метод определения передаточной функции:

Простейшим частным случаем оператора (2.1), имеющим в инженерной практике наибольшее применение, является передаточная функция вида:

. (2.2)

Определяя параметры передаточной функции, проводим касательную к кривой. Пересечение касательной с осью времени дает время запаздывания: t_о = 2,85 с. Пересечение касательной с пределом установившегося значения дает: t_о +Т_о = 11,45 = Т_о = 8,6 с. Установившееся значение есть коэффициент передачи: К_об = h_уст = 1,6; следовательно, получаем передаточную функцию:

(2.3)

График получившейся передаточной функции находится в Приложении 1.

Второй метод определения передаточной функции:

Параметры передаточной функции могут быть найдены следующим образом. Обозначив , получим:

(2.4)

где h_n и t_n – координаты точки касания, соответственно по OX и OY.

Из (2.4) определяются параметры аппроксимирующей характеристики:

Т_a = (1 - b)Т_о ; (2.5)

. (2.6)

В нашем случае: ; тогда:

Т_a = (1 – 0,25)8,6 = 6,45 с; .

После подстановки параметров передаточная функция примет вид:

; (2.7)

График получившейся передаточной функции находится в Приложении 1.

Третий метод определения передаточной функции:

Более точную аппроксимацию переходной функции ОУ даёт передаточная функция вида:

. (2.8)

Для определения параметров передаточной функции используем специальную номограмму. Так как значение параметра b выходит за пределы данной номограммы, то специально для третьей передаточной функции, воспользовавшись тем, что касательная к экспериментальной кривой проводится приблизительно, определим новые исходные параметры:

По номограмме, исходя из нового значения , находим, что 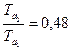; 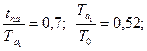тогда

(2.9)

График получившейся передаточной функции находится в Приложении 1.

Четвертый метод определения передаточной функции:

Более точную аппроксимацию переходной функции объекта управления (ОУ) даёт передаточная функция вида:

(2.10)

где

(2.11)

График получившейся передаточной функции находится в Приложении 1.

Вычислим погрешности аппроксимации всех функций. Погрешность аппроксимации может быть найдена по формуле:

, (2.12)

где S_A,i – площадь, заключённая между экспериментальной и i-той кривой; S_исх – площадь под экспериментальной кривой.

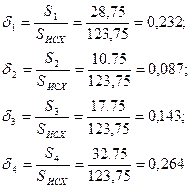
Из расчётов видно, что наименьшую погрешность аппроксимации даёт функция W_об,2 (р). Следовательно, она наилучшим образом аппроксимирует экспериментальную характеристику.

Модель опережающей части объекта управления W имеет вид:

(2.13)

Параметры этой передаточной функции находим по формулам:

После подстановки вычисленных значений в формулу (2.13), передаточная функция опережающей части объекта управления будет иметь вид:

3. Расчет параметров стабилизирующего регулятора частотным методом на ЭВМ.

Данный метод предполагает поиск оптимальных параметров алгоритма управления из условия минимума интегральной квадратичной ошибки регулирования при скачкообразном характере возмущений.

В основу метода положено представление о том, что минимуму интегрального квадратичного критерия при скачкообразном возмущении по управляющему каналу соответствуют оптимальные параметры ПИ-алгоритма и , отвечающие условиям

при ,

где - модуль АФХ замкнутой системы, т.е. амплитудно-частотная характеристика замкнутой системы по задающему воздействию.

При расчете оптимальных и используются следующие соотношения:

где - частота; A() – амплитудно-частотная характеристика (АЧХ) системы для данной частоты; - угол, заключенный между вектором АФХ объекта управления и отрицательной мнимой полуосью,

; - фазовая частотная характеристика (ФЧХ) для этой частоты; М – заданный показатель колебательности, на практике обычно принимают М=1,62.

По существу, вычисление требуемых значений и сводится к поиску такого значения , при котором отношение принимает максимальное значение. Для расчета используется часть АФХ ОУ, заключенная в 3-м квадранте. Предельное значение , ограничивающее диапазон частот для которого нужно проводить расчет, определяется из уравнения . Решая это уравнение, получаем:

. Для М = 1,62 угол = 52. Из этого условия определяется диапазон частот, для которых должен быть проведен расчет. Для этого решают относительно уравнения:

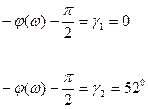
Решение первого уравнения определяет , а второго - .

Блок-схема алгоритма расчета представлена на рисунке ( 3.1).

Программа, вычисляющая оптимальные параметры ПИ-алгоритма, написана на языке Фортран.

Определяем A(), j(w) и :

Для вычисления оптимальных параметров, на ЭВМ, необходимо определить значения частот при граничных значениях, т.е в той части АФХ, которая ограничена фазами 90° и 142°.

Для этого мы строим АФХ опережающего звена, из которой и определяем вышеупомянутые значения граничных фаз.

Из АФХ определяем:

Оптимальные параметры мы будем рассчитывать в программе написанной на языке “Fortran”. Рисунок с результатами расчетов находится в Приложении 2

Получим:

Найдя оптимальные параметры, мы определяем передаточную функцию стабилизирующего регулятора:

Рис.3.1 Блок-схема алгоритма расчета.

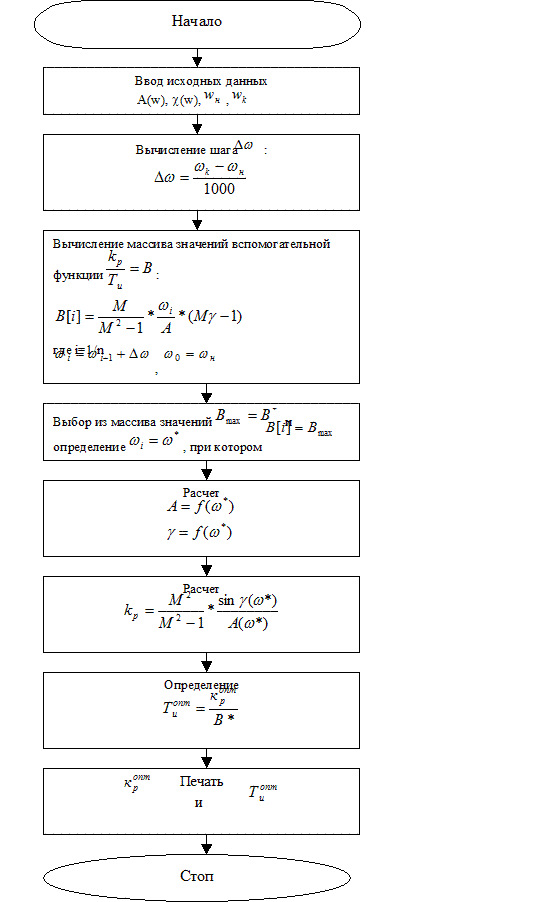
Рис 3.1. Алгоритм расчета оптимальных параметров ПИ-регулятора на ЭВМ.

4. Выбор ПИ-алгоритма управления и расчет параметров внешнего корректирующего регулятора W_р2 (p) (графоаналитическим методом Ротача).

В качестве показателя оптимальности АСР принимается минимум интеграла от квадрата ошибки системы при действии на объект наиболее тяжелого ступенчатого возмущения по регулирующему каналу (интегральный квадратичный критерий) с учетом добавочного ограничения на запас устойчивости системы, т.е.

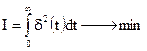. (4.1)

Такой критерий допускает значительное перерегулирование и увеличивает время регулирования, но он обеспечивает наименьшее динамическое отклонение регулируемой величины.

При практических расчетах запас устойчивости удобно характеризовать показателем колебательности системы М, значение которого в САУ, имеющих интеграл в алгоритме управления, совпадает с максимумом амплитудно-частотной характеристики системы:

где W_р. - резонансная частота, на которой А_з (w) имеет максимум.

Чтобы максимум не превышал некоторой заданной величены М, амплитудно-фазовая характеристика (АФХ) разомкнутой системы W_раз (jw) не должна заходить внутрь “запретной” области ограниченной окружностью, центр u_o и радиус R_o которой определяется через М формулами:

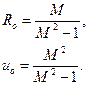
Если W_раз (jw) касается указанной окружности, то это означает, что САУ находится на границе заданного запаса устойчивости.

На практике чаще всего принимают М = 1.62. При этом в САУ перерегулирование степень затухания y=0,8-0,95.

Определяем передаточную функцию эквивалентного объекта:

где - модель опережающей части объекта управления,

- модель инерционной части ОУ,

- модель стабилизирующего регулятора

Рассчитываем параметры внешнего корректирующего регулятора графоаналитическим методом. Для чего строим АФХ модели эквивалентного объекта. Определив данные для построения, сведем их в таблицу 4.1. График АФХ находится в Приложении 3

Таблица 4.1

Данные для построения АФХ объекта.

Частота	Фаза, °	Амплитуда
0 0 0,025 0,044 0,054 0,0721 0,0875 0,106 0,14 0,172 0,23 0,279 0,338 0,411 0,45 0,498 0,605 0,666 0,809 0,98 1,19 1,44 1,75 2,34 3,8	0 -6,19 -11,05 -19,67 -23,81 -31,63 -38,1 -45,8 -60 -71,25 -90,86 -105,6 -121,23 -137,59 -145,9 -154,36 -171,27 -179,75 -196,6 -213,5 -230,2 -246,7 -262,76 -284,9 313,48	1,25 1,247 1,242 1,22 1,21 1,19 1,16 1,13 1,048 0,97 0,83 0,72 0,6 0,49 0,43 0,38 0,3 0,26 0,19 0,15 0,11 0,08 0,06 0,03 0,01

В соответствии с принятым критерием расчет оптимальных параметров алгоритма управления будет проводиться в два этапа. На первом этапе в пространстве варьируемых параметров алгоритма управления определяется область, в которой замкнутая САУ будет обладать запасом устойчивости, характеризуемым величиной М, не ниже заданного. На втором этапе в найденной области отыскивается точка, соответствующая минимуму ошибки регулирования, т.е. заданному критерию качества (условие 4.1).

Рассмотрим ПИ-алгоритм управления, передаточная функция которого имеет вид:

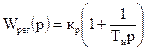, (4.2)

а параметрами, подлежащими определению, является коэффициент усиления к_р и постоянная интегрирования Т_и .

1). По АФХ объекта W_об (j) строим семейство характеристик разомкнутой системы W_раз (j) для к_р = 1 и нескольких фиксированных значений постоянной интегрирования Т_и .

Для этого сначала строим несколько векторов характеристики объекта W_об (j), например, векторы для частоты ₁ , для ₂ и т.д. К их концам надо пристроить векторы , ,…, , повернутые по отношению к векторам , ,…, на угол 90°. Длина векторов , ,…, выбирается из соотношения (где в числителе - длина вектора АФХ объекта для определенного значения частоты w_i , которую можно измерить непосредственно в миллиметрах; в знаменателе – произведение указанной частоты на фиксированное значение Т_и ). Через полученные точки С₁ , С₂ ,…, С_n проводим плавную кривую, которая является характеристикой W_раз1 (j) для выбранного значения Т_и .

Аналогичные построения проводим для других значений Т_и . В итоге получаем семейство характеристик W_раз1 (j) для различных значений Т_и .

2). Из начала координат проводим прямую ОЕ под углом b, характеризующим запас устойчивости по фазе и определяемым как

, (4.3)

3). С помощью циркуля вычерчиваем окружности с центром на отрицательной вещественной полуоси, каждая из которых касается одновременно как прямой ОЕ, так и одной из характеристик W_раз1 (j) (центр каждой окружности и ее радиус находим подбором).

4). Отношение требуемого радиуса R₀

,

к полученному в каждом отдельном случае значению r_i показывает, во сколько раз нужно изменить единичный коэффициент передачи регулятора (к_р =1), чтобы каждая характеристика W_раз1 (j) касалась окружности с заданным М , т.е.

или 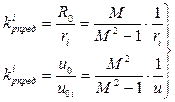. (4.4)

Для вычисления к_{р. пред} используется формула:

, (4.5)

где r – радиус, определяемый путем подбора (Приложение 3), а m-масштаб построения (в нашем случае m=0,01).

Все результаты вычислений представлены в таблице 4.2

Таблица 4.2

Ти	ri ,мм	кi
3 4 6 8	174 120 84 75	0,59 0,855 1,22 1,37

5). В результате в плоскости варьируемых параметров алгоритма к_р и Т_и строится граница области заданного запаса устойчивости, вид которой представлен в Приложении 4.

Максимум отношения к_р /Т_и , определяющее оптимальную настройку регулятора при низкочастотных возмущениях, соответствует точке пересечения касательной с границей заданного запаса устойчивости, проведенной через начало координат (точка А на рисунке в Приложении 4).

Передаточная функция регулятора, после определения координат точки А (к_р.опт = 0,855 и Т_{р опт} = 4 с), имеет вид:

Следует отметить, что найденные таким образом параметры являются оптимальными только при низкочастотном характере возмущений. По мере расширения полосы частот возмущений точка оптимума в плоскости параметров смещается вправо от точки А, при чем сначала это смещение идет вдоль границы заданного запаса устойчивости, а затем, при достаточно высокочастотных воздействиях, она вглубь области. Это означает, что с ростом частоты воздействий ПИ-алгоритм должен все более приближаться к П-алгоритму, к_р которого также снижается. Это сопровождается ухудшением эффективности управления.

5. Построение переходного процесса в системе по задающему и возмущающему воздействиям.

Переходные процессы в САУ можно рассчитать на ЭВМ частотным методом.

На первом этапе по заданной на ЭВМ передаточной функции замкнутой системы рассчитывается вещественная частотная характеристика замкнутой системы. Для этого в выражение подставляют и, меняя частоту от нуля до бесконечности, вычисляем вещественную часть :

при =0; 1;……, max.

Поскольку это выражение практически нельзя вычислить для всего диапазона частот от нуля до бесконечности, приходиться ограничиться некоторой максимальной частотой max, которая выбирается таким образом, чтобы при max вещественная частотная характеристика принимала пренебрежимо малые значения, например менее 5 % от начального значения .

Второй этап расчета заключается в получении переходного процесса по найденной на первом этапе в диапазоне . Для этого используется известное выражение

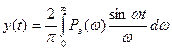при

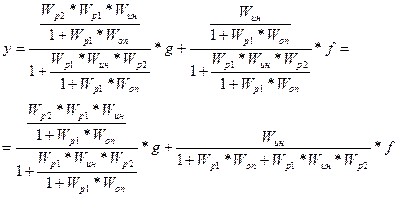Интеграл вычисляется приближенным (частотным) методом для ряда значений времени t : от t=0 до t=t_max . Максимальные значения времени выбирают таким образом, чтобы к моменту t=t_max переходной процесс y(t) практически закончился.

(5.1)

где - модель опережающей части объекта управления,

- модель инерционной части ОУ, - модель стабилизирующего регулятора

- модель внешнего корректирующего регулятора

В формуле (5.1) первое слагаемое представляет собой передаточную функцию замкнутой системы по заданию, а второе слагаемое – передаточную функцию замкнутой системы по возмущению.

Расчет переходной характеристики выполнен на ПЭВМ.

Переходные характеристики по заданию и возмущению представлены на рисунках (см. Приложение 5, 6).

Показатели качества переходных процессов.

Показатели качества переходных процессов сведены в таблицу (5.1)

Таблица (5.1)

Вид процесса	c		tр, с	d	n
По заданию	57 %	0,72	30	0	2
По возмущению	97%	0,53	44,5	0	8

c- перерегулирование

- для переходного процесса по заданию

- для переходного процесса по возмущению

y - степень затухания

- для обоих переходных процессов

t_{р - интервал времени от начала переходного процесса до момента, когда регулируемая величина попадет в зону допустимых отклонений ( » 5% от величины установившегося значения, а если речь идет о переходном процессе по возмущению, то » 5% от} ) _.

- остаточная погрешность, показывающая отклонение регулируемой величины от заданного значения по окончании неустойчивого состояния.

n – колебательность, т.е. число пересечений регулируемой величиной заданного значения за время регулирования.

По данным, приведенным в таблице (5.1), можно сделать вывод о качественности рассчитанной САУ.

6. Переход к непосредственному цифровому управлению .

Подсистема непосредственного цифрового управления (НЦУ) в основном реализуется на управляющей микро-ЭВМ, которая заменяет собой аналоговые автоматические регуляторы. В подсистеме НЦУ основные функции переработки информации выполняются комплексом средств вычислительной техники. При аналоговом исполнительном механизме (ИМ), установленным на объекте, цифровой сигнал управляющего воздействия с регулятора НЦУ с помощью ЦАП преобразуется в аналоговый сигнал, а затем подается на ИМ. Если ИМ имеет цифровой вход (шаговый двигатель), то регулятор НЦУ выдает управляющее воздействие в виде цифрового кода непосредственно на ИМ.

Непосредственное цифровое управление предусматривает выполнение следующих операций:

- опрос датчиков регулируемой величины y( t) в дискретные моменты времени, преобразование ее с помощью АЦП в цифровой код и ввода в ЭВМ;

- вычисление величины ошибки рассогласования между заданием регулятора НЦУ g и измеренным значением y ;

- определение управляющего воздействия u при помощи алгоритма управления на основе ошибки рассогласования ;

- проверка выполнения условий безопасности перед выдачей управляющего воздействия на исполнительный механизм;

- подключение выхода регулятора НЦУ на вход ЦАП, преобразование цифрового сигнала управляющего воздействия u в аналоговый сигнал, запоминания его на весь период квантования Т₀ и выдача на ИМ.

Условия безопасности контролируются в результате проверки нахождения переменных состояния в установленных пределах и приращения величины управляющего воздействия за период квантования не более определенного процента предыдущего значения.

Существующие аналоговые системы управления обладают существенными недостатками, которые устраняются при применении систем НЦУ, а именно:

1. Аналоговые системы управления (СУ) имеют ограниченную гибкость. При разработке аналоговых СУ все факторы должны быть согласованы в начальный период работы. При изменении структуры СУ необходим перемонтаж оборудования.

В системе НЦУ математические принципы управления реализуются на ЦВМ с высоким быстродействием в режиме разделения времени между всеми контурами управления. С помощью УВМ осуществляются опрос сигналов датчиков, вычисляются управляющие сигналы по заданному закону, а затем выдаются на исполнительные механизмы. Период опроса и выдачи изменяется в зависимости от динамических параметров процесса от долей до нескольких десятков секунд. Законы управления в системах НЦУ могут быть такими же, как и в аналоговых системах управления, но могут быть значительно сложнее. Изменения в управлении осуществляются программным путем за счет изменения последовательности действий операций, поэтому много стратегий управления могут быть запрограммированы и храниться одновременно в общей памяти.

2. В аналоговых СУ наблюдается дрейф выходного сигнала регулятора при неизменном сигнале на входе вследствие изменения напряжения источников питания, температуры, влажности, и т.д.

В системе НЦУ дрейф отсутствует, так как расчеты, выполняемые в УВМ при определении управляющих воздействий, не зависят от изменения внешних условий.

3. Замкнутую аналоговую СУ невозможно построить при отсутствии датчика для измерения управляемой величины.

В системах НЦУ при отсутствии необходимых датчиков для измерения управляемых параметров (состава, концентрации, качества продукта) можно измерение параметра заменить вычислением его по математической модели.

4. Условия работы ТОУ непрерывно изменяются, при этом необходима адаптивная настройка параметров или изменение структуры регулятора в соответствии с принятым критерием. В аналоговых СУ адаптивную настройку регуляторов осуществить технически очень трудно.

Системы НЦУ обладают большой гибкостью. Структура контуров НЦУ легко изменима, так как конструирование контура выполняется программными средствами. При изменении динамических параметров объекта управления оптимальные параметры регуляторов НЦУ могут рассчитываться автоматически по заданному критерию.

5. Недостатки датчиков (нелинейность характеристики, наличие сдвига нуля и зоны нечувствительности) в аналоговых СУ компенсировать технически трудно. В системах НЦУ указанные недостатки датчиков можно компенсировать программным путем.

В системах НЦУ меры по соблюдению техники безопасности в особо важных контурах управления осуществляются с меньшими затратами. При разработке систем НЦУ необходимо решать следующие задачи:

– выбор алгоритма НЦУ (закон управления исполнительными механизмами);

– определение периода квантования (опроса датчиков и выдачи управляющих воздействий), входных и выходных сигналов;

– тип управляющей ЦВМ;

– требование к устройству связи с объектом и др.

На экономическую эффективность системы НЦУ в основном влияют решение двух первых задач. Первая задача определяет точность управления параметрами объекта и затраты машинного времени, затрачиваемого на каждый контур НЦУ при одном периоде квантования. От решения второй задачи зависит загрузка УВМ операциями управления.

Система автоматического регулирования с НЦУ (рис.6.1) содержит объект управления и автоматический регулятор. Роль последнего выполняет ЭВМ, снабженная рядом устройств для преобразования сигналов из аналоговой формы в цифровую (АЦП), а также из цифровой формы в аналоговую (ЦАП). На рис.6 аналоговые сигналы обозначены как функции времени y( t), g( t), z( t). Соответствующие цифровые сигналы отличаются от них не только формой представления величин, но и дискретным характером изменения во времени. Изменение значений цифровых сигналов производится в моменты времени t = iT_д. , где Т_{д .} – интервал дискретности; i = 0,1,2,…

Цифровые сигналы обозначены на схеме как переменные с индексами y[ n], g[ n], z[ n], причем y[ n]= y( nT_д. ) ; g[ n]= g( nT_д. ) ; z[ n]= z( nT_д. ). Интервал дискретности Т_{д .} выбирается из условия Т_д. =Т_и /20 = 0,05 , где Т_и – постоянная времени интегрирования непрерывного регулятора.

u[n]

ЭВМ

АЦП

ЦАП

g(t) g[n] u(t) y(t)

АЦП

y[n] z[n] z(t)

АЦП

Рис.6.1 Структурная схема системы НЦУ.

Алгоритм работы ЭВМ, осуществляющий автоматическое регулирование, может быть получен из уже найденного закона регулирования непрерывного

регулятора.

Принимаем за исходный ПИ-закон:

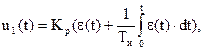(6.1)

где u₁ (t) – регулирующее воздействие на объект; e(t) – сигнал ошибки,

e(t) = g(t) – y(t); К_р и Т_и – параметры настройки непрерывного ПИ-регулятора.

Замена непрерывных сигналов цифровыми, взятыми в дискретные моменты, может быть проведена по следующей схеме:

e(t) ® e[n]; u₁ (t) ® u₁ [n];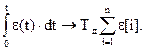

Поэтому ПИ-закон регулирования в цифровой форме имеет вид:

(6.2)

Более удобна для реализации на ЭВМ другая, так называемая скоростная форма этого алгоритма. Для её получения запишем значение u₁ на предыдущем интервале дискретности:

Вычитая его из предыдущего, получим:

Отсюда:

- постоянная времени стабилизирующего регулятора (=0,61)

К_р1 – коэффициент усиления стабилизирующего регулятора (К_р1 =1,4)

Следовательно

После подстановки e[n] = х[n] – z[n] ; e[n-1] = x[n-1] – z[n-1], получим:

(6.3)

В свою очередь:

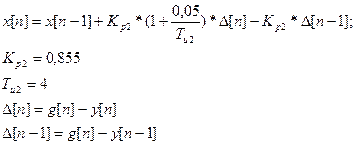
Подставляя, получаем выражение для х[n]:

(6.4)

Подставляя формулу (6.4) в (6.3), получим выражение для составления программы НЦУ.

Алгоритм непосредственного цифрового регулирования (рис.6.2), кроме расчёта управляющего воздействия, выполняет следующие дополнительные функции:

1) анализ входных сигналов и вычисленных управляющих сигналов на корректность (на схеме алгоритма – “Анализ”);

2) сигнализация о некорректных значениях и недопустимых отклонениях (на схеме – “Сигнализация”).

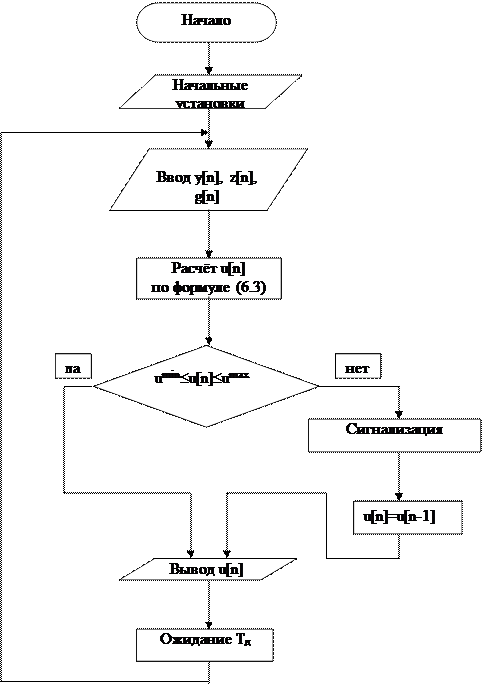Рис.6.2. Схема алгоритма НЦУ.

Заключение

В данной работе выполнен синтез каскадной САУ техническим объектом, заданным в форме экспериментальных переходных характеристик. Произведен выбор математической модели объекта управления в форме передаточных функций по управляющему каналу, выбран ПИ алгоритм управления и произведен расчет параметров ПИ-регулятора графоаналитическим методом. Построены кривые переходных процессов в системе и определены показатели качества. Осуществлен переход от аналогового (непрерывного) регулятора к НЦУ.

Список используемой литературы .

1. Дудников Е.Г. Автоматическое управление в химической промышленности. М.: Химия, 1987. 327 с.

2. Теория автоматического управления: Программа, методические указания, контрольные задания и задания к курсовой работе / ЛГИ Сост.: В.И. Златкин, С.В. Стороженко. СПб, 1992г. 40 с.

3. Изерман Р. Цифровые системы управления. Пер. с англ. М. : Мир, 1984.541 с.

4. Клюев А С., Глазов Б. В., Дубровский А. Х. Проектирование систем автоматизации технологических процессов М. : Энергия, 1980. 512 с.

5. Ротач В. Я., Шавров А. В., Бутырев В. П. Синтез алгоритмов машинного расчета оптимальных параметров систем регулирования // Теплоэнергетика. 1977. № 12. С. 76 - 79

Скачать архив с текстом документа