Системи числення
СОДЕРЖАНИЕ: МІНІСТЕРСТВО ОСВІТИ УКРАЇНИ Бердичівський політехнічний коледж Контрольна робота «Комп’ютерна схемотехніка» (варіант №21) студента групи Пзс-503МІНІСТЕРСТВО ОСВІТИ УКРАЇНИ
Бердичівський політехнічний коледж
Контрольна робота
«Комп’ютерна схемотехніка»
(варіант №21)
студента групи Пзс-503
Михайлуса Михайла Геннадійовича
2008 р.
1. Принципи побудови систем числення, основні поняття
У числової інформації в персональних комп’ютерах є такі характеристики:
1. система числення - двійкова, десяткова та інші;
2. вид числа - дійсні, комплексні та масиви;
3. тип числа - змішані, цілі та дробові;
4. форма представлення числа (місце розташування коми) - з природною (змінною), з фіксованою та з плаваючою комами;
5. розрядна сітка та формат числа;
6. діапазон і точність подання числа;
7. спосіб кодування від’ємних чисел - прямий, обернений чи доповняльний код;
8. алгоритм виконання арифметичних операцій.
Системи числення — це сукупність прийомів та правил запису чисел за допомогою цифр чи інших символів. Запис числа у деякій системі числення називається його кодом.
Усі системи числення поділяють на позиційні та непозиційні .
Непозиційна система числення має необмежену кількість символів. Кількісний еквівалент кожного символу постійний і не залежить від позиції. Найвідомішою непозиційною системою числення є римська. В якій використовується сім знаків: I -1, V - 5, X - 10, L - 50, C - 100, D - 500, M - 1000. Недоліки непозиційної системи числення: відсутність нуля, складність виконання арифметичних операцій. Хоча римськими числами часто користуються при нумерації розділів у книгах, віків в історії та інше.
Позиційна система числення має обмежену кількість символів і значення кожного символу чітко залежить від її позиції у числі. Кількість таких символів q, називають основою позиційної системи числення. Головна перевага позиційної системи числення - це зручність виконання арифметичних операцій.
У системах числення з основою меншою 10 використовують десяткові цифри, а для основи більшої 10 добавляють букви латинського алфавіту.
У позиційних системах числення значення кожного символу (цифри чи букви) визначається її зображенням і позицією у числі.
Окремі позиції в записі числа. називають розрядами , а номер позиції - номером розряду. Число розрядів у записі числа, називається його розрядністю і зберігається з довжиною числа.
Позиційні системи числення діляться на однорідні та неоднорідні .
Неоднорідні системи числення - це такі позиційні системи числення, де для кожного розряду числа основа системи числення не залежить одна від одної і може мати будь-яке значення.
Прикладом є двійково-п’ятиркова система числення (система зі змішаними основами). Вони використовуються у спеціалізованих ЕОМ ранніх поколінь.
Однорідна позиційна система числення - це така система числення, для якої множина допустимих символів для всіх розрядів однакова. Причому, якщо вага в розряді числа складає ряд геометричної прогресії з знаменником (основою р ), то це однорідна позиційна система числення з природною порядковою вагою. У даній позиційній системі числення з природною порядковою вагою число може бути представлене у вигляді поліному:
![]()
де ![]() - основа системи числення;
- основа системи числення;
![]() - вага позиції;
- вага позиції;
![]() - цифри в позиціях числа;
- цифри в позиціях числа;
![]() - номер розрядів цілої частини;
- номер розрядів цілої частини;
![]() - номер розрядів дробової частини.
- номер розрядів дробової частини.
Система числення з основою 10 - десяткова система . Для її зображення використовують цифри: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Число десять є складеним. Кожне десяткове число можна розкласти по ступенях основи десяткової системи числення. Наприклад, число 5213,6 можна представити як поліном, кожен член якого є добутком коефіцієнта на основу системи числення в деякій степені:
5213,6=5·103 +2·102 +1·101 +3·100 +6·10-1
Система числення з основою 2 - двійкова система . Для її зображення використовують цифри: 0, 1. Кожне двійкове число можна розкласти по ступенях основи двійкової системи числення. Наприклад, число 111,01 можна представити як поліном, кожен член якого є добутком коефіцієнта на основу системи числення в деякій степені:
111,012 =1·22 +1·21 +1·20 +0·2-1 +1·2-2 =7,2510
Система числення з основою 8 - вісімкова система . Для її зображення використовують цифри: 0, 1, 2, 3, 4, 5, 6, 7. Кожне вісімкове число можна розкласти по ступенях основи вісімкової системи числення. Наприклад, число 45,21 можна представити як поліном, кожен член якого є добутком коефіцієнта на основу системи числення в деякій степені:
45,218 =4·81 +5·80 +2·8-1 +1·8-21 =37,265110
Система числення з основою 16 - шістнадцяткова система . Для її зображення використовують цифри: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 та літери: A, B, C, D, E, F. Кожне шістнадцяткове число можна розкласти по ступенях основи шістнадцяткової системи числення. Наприклад, число DE,1B можна представити як поліном, кожен член якого є добутком коефіцієнта на основу системи числення в деякій степені:
DE,1B16 =D·161 ·+E·160 +1·16-1 ·B·16-2 =222,105110
Ці записи показують один із способів переведення не десяткових чисел у десяткові.
При однаковій розрядності у системах числення з більшою основою можна записати більше різних чисел.
Перевагою двійкової системи числення є: простота виконання арифметичних операцій, наявність надійних мікроелектронних схем з двома стійкими станами (тригерами), призначеними для зберігання значень двійкового розряду цифр 0 або 1.
Для переведення цілого числа з однієї системи в іншу необхідно поділити перевідне число на нову основу за правилом початкової системи. Одержана перша остача є значенням молодшого розряду в новій системі, п першу частку необхідно знову ділити. Цей процес продовжується аж до появи неподільної частки. Результат записують у порядку оберненому їхньому одержанню:
Наприклад: переведемо число 118 з десяткової системи у війкову
11810 =11101102
| 118 |
2 |
|||
| 118 |
59 |
2 |
||
| 0 |
58 |
29 |
2 |
|
|
|
1 |
28 |
14 |
2 |
| 1 |
14 |
7 |
2 |
|
| 0 |
6 |
3 |
2 |
|
| 1 |
2 |
1 |
2 |
|
| 1 |
0 |
0 |
||
| 1 |
Для переведення правильного дробу з однієї системи числення в іншу необхідно діючи за правилами початкової системи помножити перевідне число на основу нової системи. Від результату відокремити цілу частину, а дробову частину, яка залишилася знов помножити на цю основу.
Процес такого множення повторюється до одержання заданої кількості цифр. Результат записують як цілі частин добутку у порядку їхнього одержання.
Наприклад: переведемо число 0,625 з десяткової системи у двійкову
0,62510 =0,10102
| 0,625 |
|
| 2 |
|
| 1 ,250 |
|
| 2 |
|
| 0 ,500 |
|
| 2 |
|
| 1 ,000 |
|
| 2 |
|
| 0 ,000 |
Для переведення змішаних чисел у двікову систему потрібно окремо переводити цілу та дробову частини.
У вісімкових і шістнадцятькових чисел основа кратна степеню 2, тому переведення цих чисел у двійкову реалізується наступним чином: кожну цифру записують трьома двійковими цифрами (тріадами) для вісімкових чисел і чотирма - для шістнадцяткових чисел в напрямках вліво та вправо від коми. При цьому крайні незначущі нулі опускаються.
3 0 5, 4 2
Наприклад: 305,428 =11 000 101,100 012
7 2 А, E F
72А,EF16 =111 0010 1010,1110 11112
Для переведення двійкового числа у вісімкове початкове число розбивають на тріади вліво та вправо від коми, відсутні крайні цифри доповнюють нулями, кожну тріаду записують вісімковою цифрою. Аналогічно здійснюється переведення двійкового числа у шістнадцяткове, при цьому виділяють, які заміняють шістнадцятковими цифрами.
6 3, 4 2
Наприклад:
110 011,100 0102 =63,42
3 А С 7
0011 1010,1100 01112 =3А,С716
Критерії вибору
На відміну від аналогових машин, де будь-яка фізична чи математична величина може бути представлена у виді напруги, переміщення і т. п., у цифрових обчислювальних машинах дані задаються у виді цифрових чи буквених символів. При цьому використовується не будь-який набір символів, а визначена система. В електронних обчислювальних машин застосовуються позиційні системи числення. Така система числення, як римська, непозиційна, в обчислювальній техніці не використовується через свою громіздкість і складні правила утворення.
Від вибору системи числення залежить швидкодія ЕОМ та об’єм пам’яті. При виборі враховують такі нюанси:
1) наявність фізичних елементів;
2) економічність системи числення (чим більша основа системи числення, тим потрібна менша кількість розрядів, але більша кількість відображуючих елементів). Найбільш ефективна це трійкова система числення, але двійкова система і системи числення з основою 4 - не гірша;
3) важкість виконання операцій (чим менше цифр, тим простіше);
4) швидкодія (чим більше цифр, тим менша швидкодія);
5) наявність формального математичного апарату для аналізу і синтезу обчислювальних пристроїв.
Класична двійкова система числення - це така система числення, в якій для зображення чисел використовують тільки два символи: 0 та 1, а вага розрядів змінюється по закону 2k , де к —довільне число.
Правило виконання операцій у класичній двійковій системі числення
У загальному вигляді двійкові числа можна представити у вигляді поліному:
А2 = r n *2n + r n-1 * 2n-1 + … + r1 * 21 + r0 *20 + r-1 * 2-1 ,
Додавання у двійковій системі числення проводиться по правилу додавання поліномів, тобто j-тий розряд суми чисел a та b визначається за формулою.
Двійкова арифметика, чи дії над двіковими числами, використовують наступні правила, задані таблицями додавання, віднімання, множення.
Додавання Віднімання Множення
0 + 0 = 0 0 – 0 = 0 0 * 0 = 0
0 + 1 = 1 1 – 0 = 1 0 * 1 = 0
1 + 0 = 1 1 – 1 = 0 1 * 0 = 0
1 + 1 = 10 10 – 1 = 1 1 * 1 = 1
Логічне додавання
| 0 |
1 |
|
| 0 |
0 |
1 |
| 1 |
1 |
1 |
Додавання по модулю 2
|
|
0 |
1 |
| 0 |
0 |
1 |
| 1 |
1 |
0 |
Додавання двох багаторозрядних двійкових чисел проводиться порозрядно з урахуванням одиниць переповнення від попередніх розрядів.
Приклад:
| + |
1011 |
| 1011 |
|
| 10110 |
Віднімання багаторозрядних двійкових чисел, аналогічно додаванню, починається з молодших розрядів. Якщо зайняти одиницю в старшому розряді, утвориться дві одиниці в молодшому розряді.
Приклад.
| - |
1010 |
| 0110 |
|
| 0100 |
Множення являє собою багаторазове додавання проміжних сум і зсувів.
Приклад.
| x |
10011 |
| 101 |
|
| + |
10011 |
| 00000 |
|
| 10011 |
|
| 1011111 |
Перевірка за вагами розрядів числа 1011111(2) дає 64 + 16 + 8 + 4 + 2 + 1 = 95(10).
Процес ділення складається з операцій віднімання, що повторюють.
Приклад.
| 101010 |
111 |
|||
| 111 |
110 |
|||
| 0111 |
||||
| 111 |
||||
| 0000 |
||||
Позиційні системи числення з непостійною штучною вагою
Для ЦОМ розроблені допоміжні системи числення, що одержали назву двійково-кодовані десяткові системи (ДКДС). У цій системі кожна десяткова цифра представляється двійковим еквівалентом. Чотирьохрозрядне двійкове число може мати ваги розрядів: 2, 4, 2, 1 чи 8, 4, 2, 1, і ін. Десяткове число 7 у залежності від прийнятої системи ваги війкового розряду буде зображено у виді:
А) 1101 і Б) 0111
2421 8421(2-10)
Недоліком ДКДС є використання зайвих двійкових розрядів для десяткових чисел від 0 до 7. Більш раціональне застосування вісімкової системи, але вісімкові числа доводиться переводити в десяткові, а числа в ДКДС відразу читаються в десятковому коді.
Такі системи числення найчастіше використовуються в спеціалізованих ЕОМ як коди. Прикладом є двійково-десяткова системи числення.
Щоб перекласти десяткове число у двйково-десяткову систему числення, необхідно кожну цифру десяткового числа замінити.
Щоб перекласти число з двійково-десяткової системи числення необхідно спочатку перекласти його у десяткову систему числення, а потім за загальним правилом в іншу систему числення.
Щоб перекласти двійково-десяткове число у десяткову систему числення, необхідно кожні чотири цифри двійкової системи числення замінити однією цифрою десяткової системи числення, для цілої частини, починаючи з молодшого розряду, для дробової - з старшого.
Таблиця кодів
| (10) |
8-4-2-12 |
8-4-2-1 (спеціалізована) |
8-4-2-1+”3” |
8-4-2-1+”6” |
Грея |
| 0 |
0000 |
0000 |
0011 |
0110 |
0000 |
| 1 |
0001 |
0001 |
0100 |
0111 |
0001 |
| 2 |
0010 |
0010 |
0110 |
1000 |
0011 |
| 3 |
0011 |
0011 |
0111 |
1001 |
0010 |
| 4 |
0100 |
0100 |
1000 |
1010 |
0110 |
| 5 |
0101 |
1011 |
1001 |
1011 |
0111 |
| 6 |
0110 |
1100 |
1001 |
1100 |
0101 |
| 7 |
0111 |
1101 |
1010 |
1101 |
0100 |
| 8 |
1000 |
1110 |
1011 |
1110 |
1100 |
| 9 |
1001 |
1111 |
1100 |
1111 |
1101 |
2. Визначення та призначення тригерів. Класифікація тригерів
Тригери - це мікроелектроні схеми з двома стійкими станами. Вони призначені для зберігання значень двійкового розряду цифр 0 або 1.
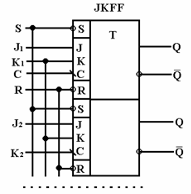
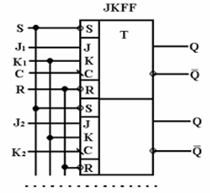
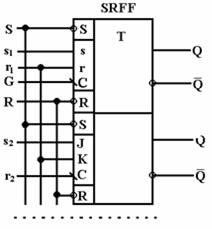
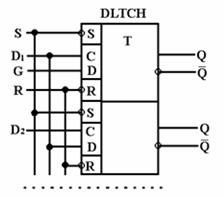
Тригери мають динамічне і потенційне керування. Кожен компонент може містити один чи кілька тригерів у корпусі, у яких загальними є сигнали установки, скидання і тактової синхронізації (дивись малюнок). Перелік тригерів приведений нижче у таблиці.
а)
б)
в)
г)
Мал.- Тригери: а) - JK-тригер з негативним фронтом спрацьовування і низьким рівнем сигналів установки і скидання; б) - D-тригер з позитивним фронтом спрацьовування і низьким рівнем сигналів установки і скидання; в) - синхронний двотактний RS-тригер; г) -синхронний однотактний D-тригер
Таблиця. Перелік тригерів
| Тип |
Параметри |
Порядок перерахування виводів |
Функціональне призначення |
|
| Тригери з динамічним керуванням |
||||
| JKFF |
Кількість тригерів |
S,R,C,J,J,...,K,K,...,Q,Q,..., Q, Q,... |
JK-тригер з негативним фронтом спрацьовування і низьким рівнем сигналу установки і скидання |
|
| DFF |
Кількість тригерів |
S, R, C, D, D,..., Q, Q,..., Q, Q,... |
D-тригер з позитивним фронтом спрацьовування і низьким рівнем сигналу установки і скидання |
|
| Тригери з потенційним управлінням |
||||
| SRFF |
Кількість тригерів |
S, R, G, S, S,..., R, R,...,Q,Q,..., Q,Q,... |
Двотактний синхронний RSтригер |
|
| DLTCH |
Кількість тригерів |
S,R,G,D,D,..., Q, Q,..., Q, Q,... |
Однотактний синхронний Dтригер |
|
Моделі динаміки тригерів з динамічним керуванням мають формат:
MODEL імя моделі UEFF [(параметри)]
Параметри моделі тригерів з динамічним керуванням типу UEFF приведені нижче в таблиці (значення за замовчуванням - 0, одиниця виміру - c). Коса риса / означає чи; наприклад, запис S/R означає сигнал S чи R.
Моделі динаміки тригерів з потенційним керуванням має формат:
MODEL імя моделі UGFF [(параметри)]
Параметри моделі тригерів з потенційним керуванням типу UGFF приведені в таблиці 5 (значення за замовчуванням - 0, одиниця виміру с).
За замовчуванням у початковий момент часу вихідні стани тригерів прийняті невизначеними (стани X). Вони залишаються такими до подачі сигналів чи установки чи скидання переходу тригера у визначений стан. У МС5 мається можливість установити визначений початковий стан за допомогою параметра DIGINITSTATE діалогового вікна Global Settings.
У моделях тригерів маються параметри, що характеризують мінімальні тривалості сигналів установки і скидання і мінімальну тривалість імпульсів. Якщо ці параметри більше нуля, то в процесі моделювання обмірювані значення длительностей імпульсів порівнюються з заданими даними і при наявності занадто коротких імпульсів на екран видаються попереджуючі повідомлення.
Завдання №1
1. Перевести 121,37 з десяткової системи числення у двійкову: 121,3710 =1111001,01012
| 121 |
2 |
0,37 |
|||
| 120 |
60 |
2 |
2 |
||
| 1 |
60 |
30 |
2 |
0 ,74 |
|
|
|
0 |
30 |
15 |
2 |
2 |
| 0 |
14 |
7 |
2 |
1 ,48 |
|
| 1 |
6 |
3 |
2 |
2 |
|
| 1 |
2 |
1 |
2 |
0 ,96 |
|
| 1 |
0 |
0 |
2 |
||
| 1 |
1 ,92 |
вісімкову: 121,3710 =171,27538
| 121 |
8 |
0,37 |
||
| 120 |
15 |
8 |
8 |
|
| 1 |
8 |
1 |
8 |
2 ,96 |
|
|
7 |
0 |
0 |
8 |
| 1 |
7 ,68 |
|||
| 8 |
||||
| 5 ,44 |
||||
| 8 |
||||
| 3 ,52 |
шістнадцяткову: 121,3710 =79,5ЕВ816
| 121 |
16 |
0,37 |
|
| 112 |
7 |
16 |
16 |
| 9 |
0 |
0 |
5 ,92 |
|
|
7 |
16 |
|
| 14 ,72 |
|||
| 16 |
|||
| 11 ,52 |
|||
| 16 |
|||
| 8 ,32 |
двійково-десяткову: 121,3710 =1 0010 0001,0011 01112-10
2. Перевести з двійкової системи числення у десяткову:
110111002 =1·27 +1·26 +0·25 +1·24 +1·23 +1·22 +0·21 +0·20 = +1·128+1·64+0·32+1·16+1·8+1·4+0·2+0·1=128+64+0+16+8+4+0+0=22010
вісімкову: 110111002 =011 011 1002 =3348
шістнадцяткову: 110111002 =1101 11002 =DC16
Завдання №2
1. записати всі константи одиниці;
2. записати всі константи нуля;
3. записати досконалу диз’юнктивну нормальну форму;
4. записати досконалу кон’юктивну нормальну форму;
5. мінімізувати функцію за допомогою карт Карно;
6. побудувати комбінаційну схему заданої функції у базисі І-ЧИ-НЕ
| Х1 |
Х2 |
Х3 |
Х4 |
f |
константа 1 |
константа 0 |
| 0 |
0 |
0 |
0 |
1 |
x1 x2 x3 x4 |
|
| 0 |
0 |
0 |
1 |
1 |
x1 x2 x3 x4 |
|
| 0 |
0 |
1 |
0 |
1 |
x1 x2 x3 x4 |
|
| 0 |
0 |
1 |
1 |
1 |
x1 x2 x3 x4 |
|
| 0 |
1 |
0 |
0 |
0 |
x1 x2 x3 x4 |
|
| 0 |
1 |
0 |
1 |
0 |
x1 x2 x3 x4 |
|
| 0 |
1 |
1 |
0 |
0 |
x1 x2 x3 x4 |
|
| 0 |
1 |
1 |
1 |
1 |
x1 x2 x3 x4 |
|
| 1 |
0 |
0 |
0 |
1 |
x1 x2 x3 x4 |
|
| 1 |
0 |
0 |
1 |
1 |
x1 x2 x3 x4 |
|
| 1 |
0 |
1 |
0 |
0 |
x1 x2 x3 x4 |
|
| 1 |
0 |
1 |
1 |
1 |
x1 x2 x3 x4 |
|
| 1 |
1 |
0 |
0 |
0 |
x1 x2 x3 x4 |
|
| 1 |
1 |
0 |
1 |
1 |
x1 x2 x3 x4 |
|
| 1 |
1 |
1 |
0 |
0 |
x1 x2 x3 x4 |
|
| 1 |
1 |
1 |
1 |
1 |
x1 x2 x3 x4 |
ДДНФ: F = x1 x2 x3 x4 x1 x2 x3 x4 x1 x2 x3 x4 x1 x2 x3 x4 x1 x2 x3 x4 x1 x2 x3 x4 x1 x2 x3 x4 x1 x2 x3 x4 x1 x2 x3 x4 x1 x2 x3 x4
ДДКНФ: F = (x1 x2 x3 x4 ) (x1 x2 x3 x4 ) (x1 x2 x3 x4 ) (x1 x2 x3 x4 ) (x1 x2 x3 x4 ) (x1 x2 x3 x4 )
|
|
|
01 |
11 |
10 |
||
| 00 |
1 |
1 |
1 |
1 |
||
| 01 |
1 |
|||||
| 11 |
1 |
1 |
||||
| 10 |
1 |
1 |
1 |
МДНФ: F = x1 x2 x3 x4 x1 x3 x4 x1 x2 x3
Комбінаційна схема:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() x1
x1
![]()
![]()
![]()
![]() x2
x2
![]()
![]()
![]() x3
x3
![]()
![]() x4
x4
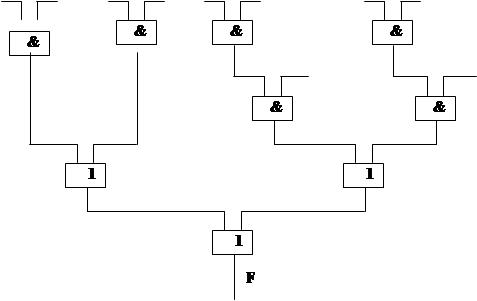 |
|||
Список використаної літератури
1. Комп’ютерна схемотехніка. М.П.Бабич, І.А.Жуков. МК-Прес. 2004 рік.
2. Конспект лекцій.
3. Інтернет.
 00
00