Системы случайных величин

СОДЕРЖАНИЕ: Функции распределения системы из двух случайных величин (СВ), ее числовые характеристики. Двумерная плотность вероятности как предел отношения. Условные законы распределения отдельных СВ в системе. Статистическая взаимозависимость и независимость.

Введение

В статистической радиотехнике частот приходится иметь дело одновременно с несколькими случайными величинами, например, мгновенные значения напряжения на выходах антенной решетки при воздействии на ее вход сигналов и помех и т.д. Свойства системы нескольких СВ не исчерпываются свойствами отдельной СВ, так как при этом необходимо описание связи между составляющими системы СВ.

1. Функции распределения системы из двух случайных величин

Функцией распределения системы из двух СВ называется вероятность совместного выполнения двух неравенств и :

.

По определению, функция распределения есть вероятность попадания случайной точки с координатами в квадрат с бесконечными размерами, расположенный левее и ниже этой точки на плоскости . Отдельно для каждой СВ X и Y можно определить одномерную функцию распределения, например, есть вероятность попадания в полуплоскость, расположенную левее точки с координатой x . Также и есть вероятность попадания в полуплоскость ниже точки y .

Свойства :

1) есть неубывающая функция обоих своих аргументов;

2) на - по обеим осям она равна нулю;

3) при равенстве + одного из аргументов согласно другому аргументу она превращается в одномерную функцию распределения;

4) если оба аргумента равны +, то = 1.

Вероятность попадания случайной точки в квадрат R с координатами по оси x и по оси y равна

.

существует как для непрерывных, так и для дискретных СВ.

2. Двумерная плотность вероятности

Двумерная плотность вероятности есть предел следующего отношения:

.

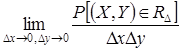Если не только непрерывна, но и дифференцируема, то двумерная плотность вероятности есть вторая смешанная частная производная функции по x и по y .

Размерность обратна произведению размерностей СВ X и Y.

Таким образом, двумерная плотность вероятности есть предел отношению вероятности попадания точки в малый прямоугольник к площади этого прямоугольника, когда оба размера прямоугольника стремятся к нулю. Геометрически можно представить как некоторую поверхность.

Если рассечь эту поверхность плоскостью, параллельной плоскости x 0y , и спроецировать полученное сечение на плоскость x 0y , то получится кривая, называемая кривой равной плотности вероятности.

Иногда удобно рассматривать семейства кривых равной плотности при разных уровнях сечения. Как и для одномерной плотности вероятности, здесь вводится понятие элемента вероятности.

Вероятность попадания случайной точки в произвольную область G определяется двумерным интегралом от по этой области. Геометрически это объем, ограниченный и областью G .

Если G есть прямоугольник с координатами вершин по оси x : и , а по оси y : и , то вероятность попадания случайной точки в этот прямоугольник определяется интегралом

.

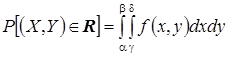Свойства двумерной плотности вероятности:

есть неотрицательная величина;

свойство нормировки аналогично одномерной плотности вероятности, но при двумерном интегрировании в бесконечных пределах.

3. Условные законы распределения отдельных СВ, входящих в систему СВ

Имея закон распределения системы двух СВ, всегда можно определить законы распределения отдельных СВ, входящих в систему. Например, и . Если известна плотность вероятности , то .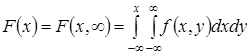

Аналогично определяется .

Таким образом, зная двумерную плотность вероятности, всегда можно определить одномерную плотность вероятности. Обратную задачу в общем случае решить невозможно. Ее можно решить, если известны условные плотности вероятности или функции распределения.

Условным законом распределения СВ, входящей в систему, называется ее закон распределения, определенный при условии, что другая СВ приняла определенное значение: . В этом случае можно найти двумерную плотность вероятности по формуле . Из этих выражений следует:

, .

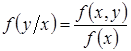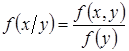4. Статистическая взаимозависимость и независимость

СВ X называется независимой от СВ Y , если закон распределения величины X не зависит от того, какое значение приняла СВ Y. В этом случае при любом y . Необходимо заметить, что если СВ X не зависит от СВ Y , то и СВ Y не зависит от СВ X . Для независимых СВ теорема умножения законов распределения имеет вид:

.

Это условие рассматривается как необходимое и достаточное условие независимости СВ. Различают понятия функциональной и статистической зависимостей. При статистической зависимости нельзя указать точно значение, которое принимает одна из СВ, если известно значение другой, можно лишь определить влияние в среднем. Но по мере увеличения взаимозависимости статистическая зависимость превращается в функциональную.

5. Числовые характеристики системы двух СВ. Коррелированность

Как и для одной СВ, для системы двух СВ можно использовать начальные и центральные моменты.

Начальным моментом порядка k, s системы (X, Y ) называется МО произведения: ; .

Центральным моментом порядка k, s системы (X, Y ) называется МО произведения k -й и s -й степени соответствующих центрированных величин.

Для непрерывных СВ –

,

.

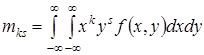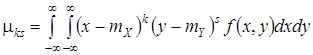Первый начальный момент есть МО для соответствующей СВ X или Y .

Аналогично имеются и вторые центральные моменты системы СВ: и , которые характеризуют степень разбросанности случайной точки вдоль осей x и y соответственно.

Особую роль в статистической радиотехнике играет второй смешанный центральный момент = K_XY - корреляционный момент.

Для непрерывных СВ корреляционный момент выражается формулой

.

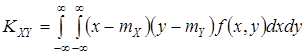Этот момент, кроме рассеивания СВ, характеризует и взаимозависимость СВ X и Y . При этом, если СВ X и Y независимы, то . Докажем это предположение: если СВ X и Y независимы, , то последний интеграл распадается на два независимых интеграла, в которых имеется произведение двух первых центральных моментов. Эти моменты равны нулю.

Чтобы исключить влияние разбросанности СВ на корреляционный момент, его делят на произведение среднеквадратических отклонений СВ X и СВ Y. Получается безразмерная величина, имеющая название коэффициент корреляции: 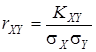. Если СВ X и СВ Y независимы, то всегда Значит, независимые СВ всегда некоррелированы, однако обратное не всегда верно. Коррелированность характеризует не всякую взаимозависимость, а лишь линейную статистическую взаимозависимость. Это означает, что при возрастании одной СВ МО другой имеет тенденцию возрастать (или убывать) в среднем по линейному закону. Коэффициент корреляции характеризует степень разбросанности координат точки относительно линейной зависимости между X и Y. Если СВ X и Y имеют линейную функциональную зависимость, то коэффициент корреляции равен ±1, в зависимости от знака наклона этой функции. При этом говорят о положительной или отрицательной корреляции.

Во многих радиотехнических устройствах имеются типовые радиотехнические тракты, состоящие из трех каскадно соединенных элементов: входной линейной цепи, нелинейного безынерционного элемента и выходной линейной цепи. В качестве этих элементов могут выступать различные электрические цепи с заданными характеристиками. На вход радиотехнического тракта воздействует аддитивная смесь сигнала и помехи:

,

где s (t ) - сигнал в виде гармонического или квазигармонического колебания; x (t ) - гауссов процесс с равномерной спектральной плотностью мощности (белый или квазибелый шум).

Известно [2], что в таких условиях при решении задачи обнаружения критерием качества работы устройства может служить отношение сигнал/помеха, которое определяется тремя выражениями:

система случайная величина

отношение сигнал/помеха по уровню 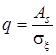, где A_s - амплитуда сигнала; - дисперсия шума;

отношение сигнал/помеха по мощности ;

энергетическое отношение сигнал/помеха 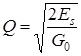, где - энергия сигнала; - спектральная плотность мощности помехи (белого или квазибелого шума).

Если длительность сигнала , то , а , где - ширина энергетической полосы квазибелого шума.

Плотность вероятности сигнала (со случайной начальной фазой)

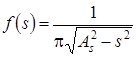, , а шума - .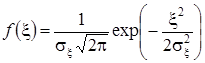

Если сигнал и помехи независимы, то , и плотность вероятности их смеси определяется интегралом свертки:

.

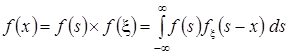6. Произвольное число СВ

Часто приходится иметь дело в статистической радиотехнике с системами многих СВ. В этом случае полной характеристикой системы СВ может служить закон распределения всей системы СВ. Например, имеется многоканальная в пространстве антенная система, с помощью которой прием ведется в нескольких точках пространства. При этом и обработка сигналов в приемных пунктах производится совместно. Для представления законов распределения системы более чем трех СВ приходится использовать многомерное пространство. Связь между функцией распределения и плотностью вероятности в этом случае обеспечивается n- мерной производной (n - число СВ, входящих в систему).

Вероятность попадания координат случайной точки в ограниченное пространство n- мерной системы определяетсяn -кратным интегрированием по этому пространству плотности вероятности.

7. Числовые характеристики системы нескольких СВ

Закон распределения системы СВ (функции распределения или плотности вероятности) является полной, исчерпывающей характеристикой системы нескольких СВ. Однако не всегда возможно применять такое описание СВ. Например, из-за ограниченности экспериментального материала или из-за того, что такое описание обладает излишней громоздкостью. Кроме того, очень часто тип распределения известен (например, n- мерный нормальный). Поэтому применяют описание системы СВ с помощью ограниченного числа числовых характеристик. К таким характеристикам относятся:

N математических ожиданий (МО), характеризующих средние значения входящих в систему СВ;

N дисперсий, характеризующих степень их разбросанности относительно своих МО;

N (N - 1 ) корреляционных моментов, определяющих попарную корреляцию СВ в системе: .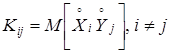

Следует отметить, что корреляционный момент при i = j превращается в дисперсию, т.е. .

Часто все корреляционные моменты располагают в виде так называемой корреляционной матрицы:

.

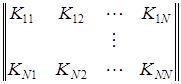По определению корреляционного момента, . Следовательно, корреляционная матрица всегда симметрическая, т.е. ее элементы, симметричные относительно диагонали, равны между собой. Обозначают ее символом . Вдоль главной диагонали располагаются дисперсии. Если все СВ, входящие в систему СВ, некоррелированы, то все элементы матрицы, кроме диагональных, равны нулю. Иногда пользуются нормированной корреляционной матрицей, составленной из коэффициентов корреляции: . Если все СВ некоррелированы, то образуется единичная матрица, у которой диагональные элементы - единицы, а недиагональные - нули.

В отношении с/п = |y (t ₀ ) |/ s_{n вых} числитель должен быть максимальным в заданный момент времени, поэтому необходимо рассматривать фазовый спектр. Так как спектр представлен в виде косинусных колебаний, они должны суммироваться на выходе цепи в фазе, чтобы максимальное мгновенное значение было при t = t ₀ , т.е. j_к (w) = -j_s (w) -wt ₀ - такие требования к фазовой характеристике обеспечат заданные требования по максимизации y (t ₀ ). Модуль передаточной функции цепи должен с точностью до постоянного множителя повторять модуль спектральной плотность сигнала K (w) = AS (w). С учетом требований к фазовой характеристике цепи K (j w) = AS (w) exp [-j j_s (w)] exp (-j wt ₀ ), так как S (j w) = S (w) exp [j j_s (w)], то K (j w) = AS (j w) exp (-j wt ₀ ).

Покажем, что найденное выражение для комплексного коэффициента передачи является оптимальным в смысле максимума отношения с/п = |y (t₀ ) |/s_{n вых} . Для линейной цепи справедлив принцип суперпозиции, т.е. можно отдельно рассматривать прохождение сигнала и шума:

|y (t ₀ ) | = | (2p) ^{- 1/2} S (j w) K (j w) exp (-j wt ₀ ) d w|,

а s_{n вых} = [ (2p) ^-1/2 W _n (w) K ² (w) d w] ^1/2 .

Подставим полученные выражения в отношение сигнал/помеха:

|y (t ₀ ) |/s_{n вых} =

= | (2p) ^-1/2 S (j w) K (j w) exp (-j wt₀ ) d w|/ [ (2p) ^-1/2 W_n (w) K ² (w) d w] ^1/2 .

В математике существует неравенство Шварца:

|F ₁ (x ) F ₂ (x ) dx |² [|F ₁ (x ) |² dx ] [|F ₂ (x ) |² dx ],

где F ₁ (x ) и F ₂ (x ) - некоторые комплексные функции. Применим это неравенство для нашего случая. Тогда отношение сигнал/помеха с/п 1/ [ (2p) ^-1 S² (w) dw] ^1/2 . Так как Э_s = (2p) ^-1 S ² (w) d w, то с/п 1/. При этом значении с/п K (j w) = K _опт (j w). Это неравенство превращается в равенство при условии, что F ₂ (x ) = F ₁ (x ). Применим это условие к K (j w), получим K _опт (j w) exp (j wt ₀ ) = AS (j w), тогда K _опт (j w) = AS (j w) exp (-j wt ₀ ).

На выходе сумматора сигнал образуется таким образом: . Возведение в квадрат является нелинейной операцией, но она выполняется уже после максимизации отношения сигнал/шум на выходах линейных согласованных фильтров и влияет незначительно.

На выходах квадратурных согласованных фильтров определяются квадраты составляющих комплексной огибающей (синусной и косинусной) и складываются в сумматоре. Полученный квадрат корреляционного интеграла инвариантен к начальной фазе входного сигнала (определяется квадрат длины вектора в комплексной системе координат). Однако наличие двух каналов приводит к потерям в отношении сигнал/шум в два раза по мощности (или - 3 дБ), поскольку шум в сумматоре удваивается по дисперсии.

Таким образом, применение синтезированной структуры приводит к независимости от начальной фазы, но приводит к усложнению согласованного фильтра (надо иметь два согласованных фильтра).

8. Двумерный нормальный закон плотности вероятности

Двумерная нормальная плотность вероятности задается формулой

,

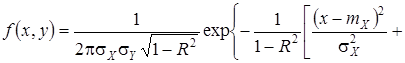
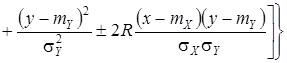в которой и - математические ожидания СВ X и Y; и - среднеквадратические отклонения этих СВ; R - коэффициент корреляции.

Заметим, что кривые равной плотности вероятности имеют вид эллипсов:

.

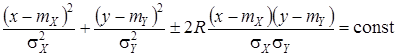На этом основании эллипсы имеют название эллипсов равных вероятностей или эллипсов рассеивания. В зависимости от знака величины R эллипсы имеют различную форму и ориентацию на плоскости x 0y. При этом главные оси эллипса пропорциональны главным среднеквадратическим отклонениям и , которые связаны со среднеквадратическими отклонениями следующими формулами:

;

,

где a - угол между одной из главных осей эллипса и осью 0x. Если главные оси эллипса совпадают с осями координат, то можно утверждать, что СВ X и Y являются некоррелированными, а главные среднеквадратические отклонения равны среднеквадратическим отклонениям. Если же при этом дисперсии и одинаковы, то эллипсы рассеивания превращаются в окружности.

Нормальное распределение имеет исключительную роль в статистической радиотехнике. Почти все шумы радиоприемных устройств подчинены нормальному закону (их мгновенные значения). Универсальность нормального закона объясняется тем, что каждая СВ, являющаяся суммой очень большого числа независимых СВ, каждая из которых оказывает незначительное влияние на сумму, распределена по нормальному закону, причем независимо от вида распределения каждого слагаемого (центральная предельная теорема теории вероятности) (рис.1).

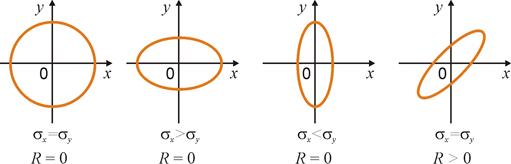
Рис.1

Поскольку в выражение для нормальной плотности вероятности входит только R , то для нормальных СВ некоррелированность одновременно означает и их независимость. Нетрудно доказать это утверждение, если в выражение для нормальной плотности вероятности подставить R= 0. При этом выражение для двумерной нормальной плотности вероятности преобразуется в произведение одномерных нормальных плотностей вероятностей.

Библиографический список

1. Математические основы современной радиоэлектроники [Текст] / И.А. Большаков [и др.]. - М.: Сов. радио, 2009. - 208 с.

2. Манжос, В.Н. Теория и техника обработки радиолокационной информации на фоне помех [Текст] / Я.Д. Ширман, В.Н. Манжос. - М.: Радио и связь, 2011. - 416 с.

3. Жовинский, В.Н. Инженерный экспресс-анализ случайных процессов [Текст] / А.Н. Жовинский, В.Н. Жовинский. - М.: Энергия, 2009. - 112 с.

4. Федосов, В.П. Статистическая радиотехника [Текст]: конспект лекций / В.П. Федосов, В.П. Рыжов. - Таганрог: Изд-во ТРТИ, 2008. - 76 с.

5. Гнеденко, Б.Н. Курс теории вероятности [Текст] / Б.Н. Гнеденко. - М.: Физматгиз, 2011. - 203 с.

Скачать архив с текстом документа