Составление теоретической конструкции балки
СОДЕРЖАНИЕ: Курсовая работа Тема: Составление теоретической конструкции балки Содержание 1 Теоретические основы создания балки 2 Создание балки из конкретного металла с заданными характеристиками
Курсовая работа
Тема: Составление теоретической конструкции балки
Содержание
1 Теоретические основы создания балки
2 Создание балки из конкретного металла с заданными характеристиками
3 Другие элементы
4 Расчет нагрузки на элементы
5 Определение размеров рам
1 Теоретические основы создания балки
1.1 Построение эпюр Qy и Mx. Опорные реакции
Yi = 0, RAy –qa+ qa– F =0,
Ray = F= 3qa = 50,4кН,
ma= 0, – МA+0,5qa2 – 1,5aqa – 2qa2 + 3qa3a = 0,
– МA+0,5qa2 – 1,5qa2 – 2qa2 +9qa2 = 0,
– MA = – 6qa2.
Эпюра Qy. Она строится по формуле Q=Q0 ±qz. В данном случае стоит взять знак «минус» для участка балки АВ, (так как погонная нагрузка направлена вниз), и знак «плюс» для участка балки ВС (погонная нагрузка направлена вверх). Поперечная сила постоянна на участке СD (т.к. q=0) и изображается прямой, параллельной оси Оz, на участках АВ и ВС – наклонной прямой (q=const). Вычисляем значения Qy в характерных точках
QA = RAy=3qa, кН,
QAB = QA – qa =3qa – qa=2qa , кН,
QВС = QAB +qa = 2qa+qa = 3qa, кН,
QСD = QВС = 3qa , кН и строим ее эпюру.
Эпюра Мх. Она строится по формуле Мх = М0+Q0z–0,5qz2. Изгибающий момент изменяется по квадратичному закону на участках АВ и ВС (т.к. q=const), и по линейному закону на участке СD (q=0). По значениям момента в характерных точках
MA = – 6qa2, кHм,
MAB = MA + Raya = – 6qa2 + 3qa2 = – 3qa2, кHм,
MBC = MAB +2qa a = – 3qa2 + 2qa2 = – qa2, кHм,
MCD = MBC – 2qa2 = – qa2– 2qa2 = – 3qa2, кHм,
MF = – 3qa2+ 3qa2=0
строим эпюру Мх. Расчетный изгибающий момент равен
Mрас = MA = 6 qa2 = 120,96 кHм.
1.2 Подбор сечений
Из условия прочности по нормальным напряжениям мах=Мрас/Wx [] определяем требуемый момент сопротивления поперечного сечения
Wx Mрас /[] = 120,96 103/160106 = 756 см3,
по которому подбираем конкретные сечения.
Круг: Wx = d3/32,
![]() =
= ![]() =19,75 см.
=19,75 см.
Принимаем по ГОСТ 6636-86 нормализованное значение d0 = 200 мм, тогда А1 = d02/4 = 202/4 =314 см2.
Прямоугольник (h/b = 2) Wx=b(2b)2/6=2b3/3,
![]() b 33 Wx /2 =
b 33 Wx /2 = ![]() = 10,43 см.
= 10,43 см.
Ближайшее меньшее значение равно b0=100мм. При этом балка будет работать с перенапряжением, равным
= [(b3-b03)/ b03] 100% =[10,433 – 103/ 103] 100% = 13,46%,
что недопустимо. Поэтому принимаем ближайший больший размер b0=105 мм, для которого А2=2b02= 2 10,52 = 220,5 см2.
Двутавр. По ГОСТ 8239-89 выбираем двутавр №36, для которого Wх=743,0 см3, А3 = 61,9 см2.
Два швеллера. По ГОСТ 8240-89 выбираем два швеллера № 30, для которых Wх = 2387 = 774 см3, А4 = 2 40,5 = 81см2.
Неравнобокие уголки. Они находятся подбором, так как в сортаменте не даны значения момента сопротивления. Используя формулу Wx=2Ix/(b – y0), сделаем несколько попыток, выбираем два уголка 250х160х20, для которых Wх = 24987/(25 – 8,31) = 597,6 см3, А5 = 278,5 = 157,0 см2.
| № |
1 |
2 |
3 |
4 |
5 |
| Форма сечения |
|
|
|
][ |
|
| А, см2 |
314 |
220,5 |
61,9 |
81 |
157 |
| A1 : A2 : A3 : A4 : A5 = 1 : 0,7 : 0,2 : 0,26 : 0,5 |
|||||
1.3 Оценка экономичности подобранных сечений
Масса балки определяется как произведение плотности материала на ее объем m=Al, т.е. расход материала при прочих равных условиях зависит только от площади поперечного сечения А. Сравнивая массы балок:
m1 : m2 : m3 : m4 : m5 = A1 : A2 : A3 : A4 : A5 = 1 : 0,7 : 0,2 : 0,26 : 0,5,
заключаем, что самым неэкономичным является круглое сечение. При замене круга другими формами (прямоугольник, двутавр, два швеллера, два уголка) достигается экономия, равная соответственно 30%, 80%, 74% и 50%.
Исследование напряжений в опорном сечении для балки двутаврового профиля №36, параметры которой по ГОСТ 8239-89 равны:
h = 36 см, b = 14,5 см, d = 0,75 см, t = 1,23 см,
Ix = 13380 см4, Sx = 423 см3.
Внутренние силовые факторы в опорном сечении А:
QA= 3qa = 3141,2 = 50,4 кН;
MA= – 6qa2 = – 6141,22 = –120,96 кНм.
Эпюра . Нормальные напряжения в поперечном сечении изменяются по линейному закону z=(Mx/Ix)y. Вычисляем напряжения в крайних точках
max= min = Mx/ Wx = 120,96 103/75610-6 = 160 МПа
и строим эпюру
Эпюра . Она строится по формуле Журавского =![]() .
.
Находим значения в 4 характерных точках по высоте сечения и строим эпюру касательных напряжений.
| № точек |
bi, см |
см3 |
|
i/ max |
i |
max |
| 1, 1 |
14,5 |
0 |
0 |
0 |
0 |
max= |
| 2, 2 |
14,5 |
310 |
21,38 |
0,04 |
0,8 |
|
| 3, 3 |
0,75 |
310 |
413,30 |
0,74 |
15,6 |
|
| 4, 4 |
0,75 |
423 |
58,34 |
1 |
21,2 |
Определение главных напряжений в точке К (ук=0,4h):
– напряжения в поперечном сечении
к = (МА/IA) YK= (–120,96103/1338010-8) 0,436102 = – 130МПа,
K = ![]() = 50,4103 33810-6 /(0,7510-213380 10-8) = 17МПа;
= 50,4103 33810-6 /(0,7510-213380 10-8) = 17МПа;
– величины главных напряжений
1,3 =0,5(к±![]() )=0,5(–130±
)=0,5(–130±![]() ),
),
1 = 2,2 МПа; 3 = – 132,2 МПа – ориентация главных площадок
tg1 = (1 – к)/k= (2,2 – ( –130))/17 = 7,78;
1 = 82040.
Экстремальные касательные напряжения равны по величине
max, min= ±0,5(1- 3)= ±0,5(2,2 + 132,2) = ± 67,2 МПа
и действуют на площадках, равнонаклоненным к осям 1 и 3. Графическое определение главных напряжений и положения главных площадок.
2 Создание балки из конкретного металла с заданными характеристиками
2.1 Построение эпюр поперечной силы и изгибающего момента. Опорные реакции
mв=0, – RA·3a + 1,5qa2 + q·3a·2,5a – 3·qa·a = 0, RA = 2qa;
Yi=0, RA – q·3a + RB – 3qa =0, RB = 4qa.
Эпюра Qy.
Поперечная сила постоянна на участке ЕВ и ВС; изменяется по линейному закону на участке DA и AE и принимает следующие значения:
QD = 0, QAD = QD – qa = – qa,
QA = QAD + RA = – qa + 2qa = qa, QAE = QA – q·2a = qa – 2qa = – qa,
QEB = QAE = – qa, QB = QEB+ RB = – qa + 4qa = 3qa,
QB = QC = 3qa.
Эпюра Мх.
Изгибающий момент изменяется по линейному закону на участке EB и BC, по квадратичному закону на участках DA и AE, принимая экстремальные значения в сечении z = 4а. По значениям момента в характерных точках
MD = 0, MA = – qa·0,5a = – 0,5qa2 ,
M (2a) = – 2qa·a + RA·a = – 2qa2 + 2qa2 = 0,
ME = – 3qa·1,5a + RA·2a = – 4,5qa2 + 4qa2 = – 0,5qa2 ,
MEB = ME + 1,5qa2 = – 0,5qa2 + 1,5qa2 = qa2 ,
Mmax = MB = – 3qa·2,5a + RA·3a – 1,5qa2 = – 3 qa2,
MC = 0.
строим эпюру Мх, из которой находим расчетный изгибающий момент
Мрас= 3qa2 = 60,48 кНм
2.2 Определение перемещений
2.2.1 Метод начальных параметров
Из граничных условий имеем: vA = 0, vB = 0. Отсюда находим v0 , 0:
vA= v(a) = v0 + 0а + ![]() ,
,
vB=v(4a)=v0+ 04а +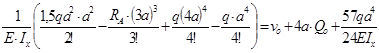 ;
;
0 = – ![]() ;
;
v0 = – ![]()
![]() = 0; v0 =
= 0; v0 = ![]() .
.
А теперь находим искомые перемещения:
- сечение z = а
(а) = 0 + ![]() ;
;
V(а) = 0;
- сечение z = 2а
(2а) = 0 + 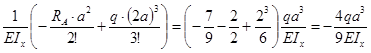 ;
;
v(2а) = v0+ 02a+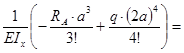
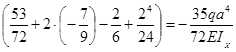 ;
;
- сечение z = 3а
(3а) = 0 + 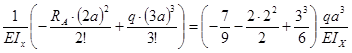 =
= ![]() ;
;
v(3a) = v0 + 03a + 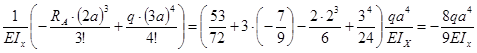 ;
;
- сечение z = 4а
v(4a) = 0;
(4а)=0+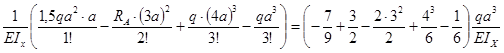 =
=![]() ;
;
- сечение z = 5а
(5а)=0+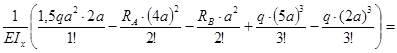
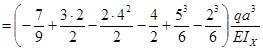 =
= ![]() ;
;
V(5a)=V0+05a+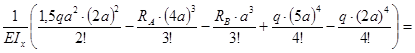
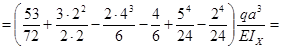
![]() .
.
Результаты вычислений сведем в таблице и построим упругую линию балки пунктиром
| Перемещения |
Сечение z |
|||||
| 0 |
a |
2a |
3a |
4a |
5a |
|
| х(qa3/EIx)-1 |
– 7/9 |
–11/18 |
– 4/9 |
– 5/18 |
20/9 |
67/18 |
| v х(qa4/EIx)-1 |
53/72 |
0 |
–35/72 |
– 8/9 |
0 |
29/9 |
Для расчета балки на жесткость необходимо знать максимальный прогиб, который имеет место в сечении, где угол поворота равен нулю. Он имеет место в сечении z = 3а, отсюда vmax= vВ = 8qa4/(9 EIx)
2.2.2.Энергетический метод
Строим эпюры моментов от заданной нагрузки и от единичных воздействий, приложенных к балке в направлении искомых перемещений. Определяем моменты посередине участков.
МсрDА = (МС + МА)/2 + qа2/8 = (0 + 1/2) qа2 + qа2/8 = 3/8 qа2,
МсрАM = (МA + МM)/2 + qа2/8 = (0 + 1/2) qа2 + qа2/8 = 3/8 qа2,
МсрME = (МM + МE)/2 + qа2/8 = (0 + 1/2) qа2 + qа2/8 = 3/8 qа2,
МсрEB =(МE + МB)/2 = (1 + 3) qа2/2 =1/2 qа2,
МсрBС =(МB + МC)/2 = (3 + 0) qа2/2 = 3/2qа2.
Перемножая соответствующие эпюры, находим искомые перемещения, увеличенные для удобства вычислений в EI раз:
EIxvB=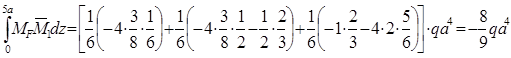 ;
;
ЕIxA=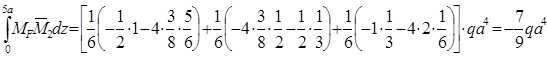 ;
;
ЕIxB=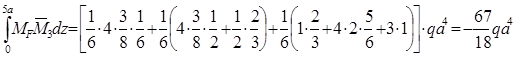 .
.
2.2.2 Расчет на ЭВМ методом конечных элементов
Исходные данные вво- дятся в безразмерной форме:
= z /a (0 10), ![]() ,
, ![]() .
.
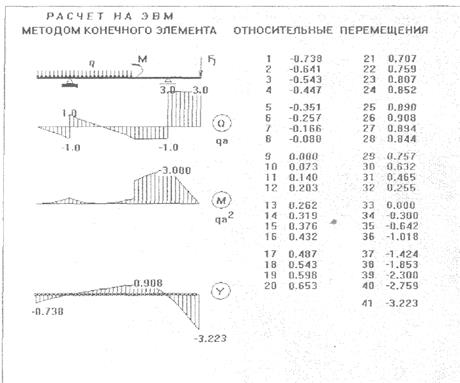
Из рисунка следует, что наибольший прогиб имеет место в сечении 3a, где возникает наибольший изгибающий момент, и равен
![]() .
.
2.2.4 Подбор сечения неравнобоких уголков по условиям прочности и жесткости
Из условия прочности имеем max = Mmax/Wx [].
Отсюда, учитывая что Mmax = – 3 qa2,
[]=![]() ,
,
вр=![]() , Fте находим из диаграммы растяжения
, Fте находим из диаграммы растяжения
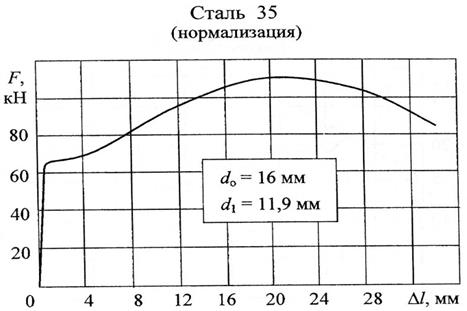
вр = ![]() = 318 МПа,
= 318 МПа,
[n] = 1,5 если ![]() 5%, [n] = 2,4 если
5%, [n] = 2,4 если ![]() 5%,
5%,
![]() =
= ![]() =0,7%,
=0,7%,
[] = 318/2,4=132,5 МПа, отсюда Wx Mmax/ []=60,48103/132,5106 = 456 см3.
Условиям прочности удовлетворяет Wx 456 см3
Согласно условиям жесткости
![]() [f],
[f],
откуда l/[f] = 900, [f] = l/900 =2,5/900 = 2,8 мм
Ix ![]() =
=![]() = 4608 см4;
= 4608 см4;
Учитывая условия прочности и жесткости по ГОСТу 8510-86 выбираем неравнобокие уголки №27 с следующими параметрами:
B=250мм, b=160 мм, d=18мм, A=157 см2, Ix=4987см4, Wx=597,6см3.
3 Другие элементы
3.1 Раскрытие статической неопределимости
Данная система дважды статически неопределима (две дополнительные связи), поэтому канонические уравнения имеют вид:
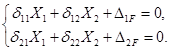
Коэффициенты при неизвестных, увеличенные в EI раз:
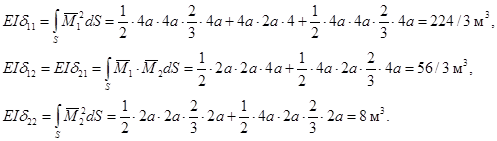
Проверка:
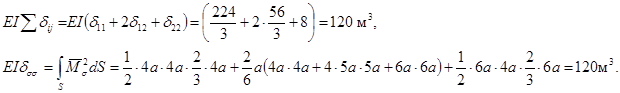
Свободные члены, увеличенные в EI раз:
![]() ;
;
![]()
Проверка: ![]() ;
;
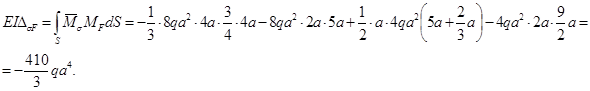
Канонические уравнения имеют вид:
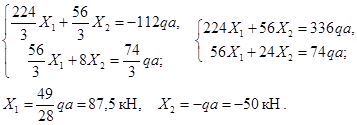
3.2 Определение опорных реакций
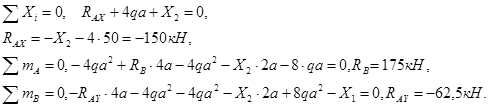
3.3 Построение эпюр внутренних силовых факторов
Эпюра Q. Эпюра строится по формуле ![]() . Вычисляем значения Q в характерных точках:
. Вычисляем значения Q в характерных точках:
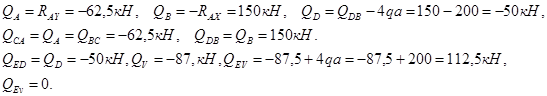
![]()
и строим эпюру Q.
Эпюра M. Эпюра строится согласно выражению
![]() .
.
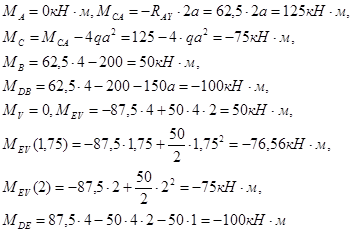
Эпюра N. Деформацию сжатия испытывают стержни BC и CD. Продольная сила в пределах каждого участка постоянна и принимает следующие значения:
![]()
3.4 Проверка решения
3.4.1Статическая проверка
Узел B
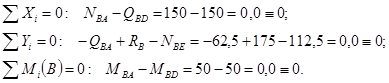
Узел C
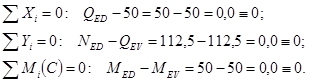
3.4.2 Кинематическая проверка. Проверка состоит в выполнении условия
![]() .
.
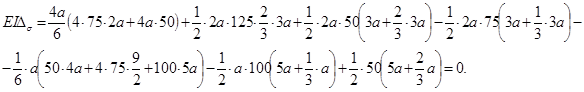
4 Расчет нагрузки на элементы
4.1 Определение геометрических характеристик сечения
а)Координаты центра тяжести.
| № п/п |
vi |
Ai |
vi Ai |
| 1 |
10t |
32t2 |
320t3 |
| 2 |
4t |
16t2 |
64t3 |
| 48t2 |
384t3 |
||
uc=0, vc=![]() =384t3/48t2=8t.
=384t3/48t2=8t.
б) Моменты инерции относительно главных центральных осей x, y.
Предварительно вычисляем осевые моменты инерции отдельных частей относительно собственных центральных осей ii
I![]() = 8t·(4t)3/12 = 42,67t4,
= 8t·(4t)3/12 = 42,67t4,
I![]() = 2·t·(8t)3/12 = 85,33t4,
= 2·t·(8t)3/12 = 85,33t4,
I![]() = 4t·(8t)3/12 = 170,67t4,
= 4t·(8t)3/12 = 170,67t4,
I![]() = 2·8t·t3/12 = 1,33t4.
= 2·8t·t3/12 = 1,33t4.
Остальные вычисления представим в табличной форме.
| № п/п |
xi |
yi |
Ai |
Ix=(I |
Iу=(I |
||||
| I |
|
I |
I |
|
I |
||||
| 1 |
0 |
2t |
32t2 |
42,67t4 |
128t4 |
213,33t4 |
1,33t4 |
0 |
1,33t4 |
| 2 |
1,5t |
-4t |
16t2 |
85,33t4 |
256t4 |
298,67t4 |
170,67t4 |
36t4 |
206,67t4 |
| 48t2 |
128t4 |
384t4 |
512t4 |
172t4 |
36t4 |
208t4 |
|||
в) Главные радиусы инерции
ix2 = Ix/A = 512t4/(48t2) = 10,67t2;
iy2 = Iy/A = 208t4/(48t2) = 4,33t2.
Построение ядра сечения. Для фигуры с прямолинейными сторонами ядро сечения представляет собой выпуклый многоугольник, координаты вершин которого определяются формулами:
xяi= – iy2/ai , yяi= – ix2/bi .
Здесь ai и bi – отрезки, отсекаемые нейтральной линией на осях координат, при ее обкатывании вокруг контура сечения. Выполняя необходимые вычисления в табличной форме, получим ядро сечения.
| Положение нейтральной линии |
Отрезки, отсекаемые на осях |
Координаты вершин ядра сечения |
||
| ai |
bi |
xяi |
yяi |
|
| 1–1 |
4t |
0 |
–2,668t |
|
| 2–2 (2–2) |
–4t (4t) |
1,083t (–1,083t) |
0 |
|
| 3–3 (3–3) |
–4t (4t) |
–16t |
1,083t (–1,083t) |
0,667t |
| 4–4 |
–8t |
0 |
1,334t |
|
4.2 Определение размеров сечения
Отрезки, отсекаемые нейтральной линией на осях координат
ао= – iy2/xf = –4,33t 2/(4t) = –1,083t;
bо= – ix2/yf = –10,67t 2/0 = .
Проводим нейтральную линию nn и устанавливаем опасные точки. Это будут точки 1 и 6 как наиболее удаленные от нейтральной оси.
Из условия прочности на растяжение
max = 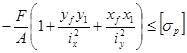 ,
,
max = ![]() ,
,
откуда 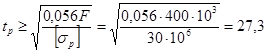 мм.
мм.
Из условия прочности на сжатие
min = 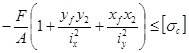 ,
,
min = ![]() ,
,
откуда 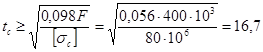
Следовательно, t = max ![]() = tp = 27,3 мм. Принимаем по ГОСТ 6636
= tp = 27,3 мм. Принимаем по ГОСТ 6636 ![]() =28 мм. Для ближайшего меньшего размера (
=28 мм. Для ближайшего меньшего размера (![]() =26 мм) будет перенапряжение 15,7%, что недопустимо.
=26 мм) будет перенапряжение 15,7%, что недопустимо.
4.3 Построение эпюры нормальных напряжений. Исходя из принятых размеров сечения, находим напряжения в опасных точках
![]() МПа;
МПа;
![]() МПа
МПа
и строим эпюру .
5 Пространственные рамы
5.1 Устанавливаем опасное сечение для каждого из стержней
AB – сечение А, где Mx = 3qa2, My = qa2, Mz = 2qa2;
Qx = 0, Qy = 2qa, NA = qa.
AB – сечение B, где Mx = qa2, My = qa2, Mz = 2qa2;
Qy =2qa, NA = qa.
BC – сечение B, где Mx = qa2, My = 2qa2, Mz = 0,5qa2;
Qy =qa, N = 2qa.
BC – сечение C, где Mx = 0, My = 2qa2, Mz = 0,5qa2;
Qy =qa, N = 2qa.
CD – сечение C, где Mx = 0,5qa2, My = 2qa2;
Qx = 2qa , Qy = qa.
CD – сечение D, где Mx = 0, My = 0;
Qx = 2qa , Qy = 0.
5.2 Подбор сечений стержней
Сечение А Стержень АВ
Он испытывает изгиб в двух плоскостях, кручение, сдвиг и сжатие.Так как Mx My, то рациональным будет такое расположение сечения, при котором Wx Wy, т.е. длинная сторона прямоугольника должна быть параллельна оси y. Для установления опасной точки необходимо вычислит эквивалентные напряжения в трех точках контура сечения. Из них опасной будет та точка, в которой экв является наибольшим. При подборе сечений будем пренебрегать в первом приближении продольными и поперечными силами.
Точка 1. В этой точке возникает линейное напряженное состояние, поэтому
![]() .
.
Так как h/b=1,5, то h = 1,5b;
![]() ,
, ![]() .
.
Следовательно,
![]() .
.
Точка 2. В этой точке возникает плоское напряженное состояние, поэтому
![]() .
.
Так как ![]() ,
, ![]() ,
,
Следовательно,
![]() .
.
Точка 3. В этой точке возникает плоское напряженное состояние, поэтому сог-ласно III гипотезе прочности
![]() .
.
Так как ![]() ,
, ![]() ,
,
Следовательно, ![]() .
.
Так как ![]() , то опасной является точка 2.
, то опасной является точка 2.
Записываем условие прочности для точки 2
![]() .
.
Отсюда ![]() мм.
мм.
Принимаем по ГОСТ 6636 bo =160 мм. Следовательно, стержень АВ должен иметь сечение 16x24 см.
Так как подбор сечения выполнен без учета продольной и поперечной сил, то необходимо проверить прочность стержня, принимая во внимание все внутренние силовые факторы, возникающие в опасном сечении. Рассмотрим опасную точку 2 и вычислим в ней нормальные, касательные и эквивалентные напряжения.
Нормальные напряжения:
- от изгиба
![]() МПа;
МПа;
- от продольной силы
![]() МПа;
МПа;
- суммарные
![]() МПа.
МПа.
Касательные напряжения:
- от кручения
![]()
![]() МПа;
МПа;
- от поперечной силы
![]() МПа;
МПа;
- суммарные
![]() МПа.
МПа.
Эквивалентное напряжение
![]() МПа.
МПа.
Без учета продольной и поперечной сил
![]() МПа.
МПа.
Как видим, расхождение между ![]() и
и ![]() не превышает 3%, т.е. лежит в пределах инженерного расчета. Поэтому на практике продольными и поперечными силами, как правило, пренебрегают.
не превышает 3%, т.е. лежит в пределах инженерного расчета. Поэтому на практике продольными и поперечными силами, как правило, пренебрегают.
Условие прочности стержня АВ при принятых размерах поперечного сечения выполняется, так как
![]() МПа.
МПа.
Сечение В Стержень ВС
Он испытывает изгиб в двух плоскостях, кручение, сдвиг и сжатие. Пренебрегая продольной и поперечной силами, условие прочности можно записать в виде ![]() ,
,
где ![]() - эквивалентный момент по III гипотезе прочности, равный
- эквивалентный момент по III гипотезе прочности, равный
![]() .
.
Следовательно, ![]() ,
,
откуда 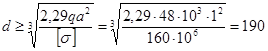 мм.
мм.
Принимаем по ГОСТ 6636 do=190мм.
Сечение С Стержень СD
Он испытывает изгиб в двух плоскостях, т.е. косой изгиб. Так как Mx My, то сечение следует расположить длинной стороной вдоль оси x. В этом случае будет выполняться условие WxWy, т.е.большему изгибающему моменту будет соответствовать больший момент сопротивления
Так как h/b=2, то h = 2b;
![]() ,
, ![]() .
.
Условие прочности
![]() .
.
Отсюда 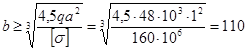 мм.
мм.
Принимаем по ГОСТу 6636 do=110мм. Искомое сечение стержня будет 11x18 см.
6 Определение размеров рам
Дано: ![]()
Значения коэффициента продольного изгиба , увеличенные в 1000 раз, приведены в таблице:
| 10 |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
90 |
100 |
110 |
120 |
130 |
140 |
150 |
|
| 996 |
992 |
900 |
780 |
660 |
575 |
463 |
387 |
312 |
252 |
210 |
175 |
150 |
129 |
113 |
6.1 Определение геометрических характеристик сечения
- площадь ![]() ;
;
- минимальный момент инерции
Imin = ![]() ;
;
- минимальный радиус инерции
![]() .
.
Полученные характеристики можно записать в общем виде следующим образом:
![]() ,
,
где ![]() ; d = а – характерный размер сечения.
; d = а – характерный размер сечения.
6.2 Подбор поперечного сечения
Искомый характерный размер сечения находится из трансцендентного уравнения
![]() ,
,
которое решается методом последовательных приближений.
Первое приближение. Примем ![]() , тогда
, тогда
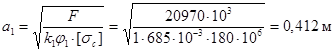
Гибкость стержня равна ![]() .
.
По таблице ![]() , используя формулу линейной интерполяции
, используя формулу линейной интерполяции
![]() ,
,
находим ![]() .
.
Ввиду большой разницы между 1 и ![]() делаем второе приближение, принимая
делаем второе приближение, принимая
Имеем: ![]() .
.
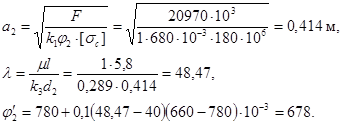
Расхождение ![]() , то есть подбор закончен. Следовательно, характерный размер сечения должен быть не менее
, то есть подбор закончен. Следовательно, характерный размер сечения должен быть не менее ![]() . Принимаем по ГОСТ 6636:
. Принимаем по ГОСТ 6636: ![]() .
.
6.3 Определение коэффициента запаса устойчивости
Гибкость стержня при принятых размерах сечения равна
![]() .
.
Поскольку ![]() , то стержень обладает средней гибкостью и для определения критической силы следует воспользоваться эмпирической формулой
, то стержень обладает средней гибкостью и для определения критической силы следует воспользоваться эмпирической формулой
![]() .
.
Коэффициент запаса устойчивости равен ![]()

