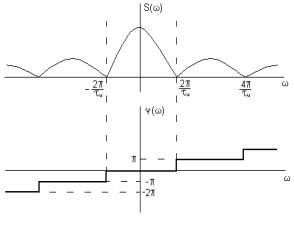
Спектры непериодических сигналов
СОДЕРЖАНИЕ: Спектры непериодических сигналов Пусть задан сигнал в виде ограниченной во времени функции s(t), отличной от нуля в промежутке t1t2. Выделим произвольный отрезок времени T, включающий промежуток t1t2, далее продолжим аналитически s(t) на всю бесконечную ось с периодом T. Тогда мы сможем разложить такую периодическую функцию s(t) в гармонический ряд Фурье.1.
2. Спектры непериодических сигналов
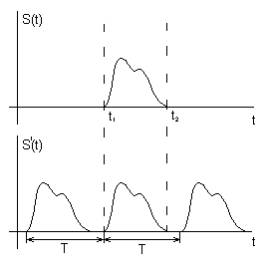 |
Пусть задан сигнал в виде ограниченной во времени функции s(t), отличной от нуля в промежутке t1 t2 . Выделим произвольный отрезок времени T, включающий промежуток t1 t2 , далее продолжим аналитически s(t) на всю бесконечную ось с периодом T. Тогда мы сможем разложить такую периодическую функцию s(t) в гармонический ряд Фурье. В комплексной форме будем иметь:
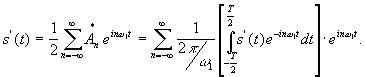
Полученный ряд на участке t1 t2 будет точно соответствовать нашей функции s(t). Однако, если нас интересуют моменты времени за участком t1 t2 , то необходимо увеличить период Т, т. е. отодвинуть повторные значения функции s(t). Производя замену переменных и переходя от суммирования к интегрированию, получим
![]()
![]()
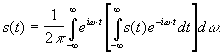
![]()
![]() где
где
![]() - спектральная плотность сигнала s(t).
- спектральная плотность сигнала s(t).
Спектр непериодического сигнала сплошной (непрерывный) и распространяется на отрицательные частоты.
Если ![]() , то
, то ![]() - модуль спектральной плотности – амплитудно-частотная характеристика.
- модуль спектральной плотности – амплитудно-частотная характеристика.
![]() - фазово-частотная характеристика.
- фазово-частотная характеристика.
![]()
Необходимое условие существования спектральной плотности ![]()
Пример. Спектр прямоугольного сигнала
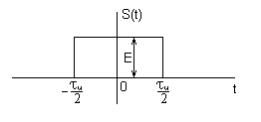 |
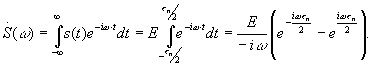
Согласно формуле Эйлера ![]()
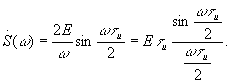
|
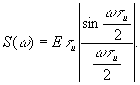
|
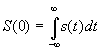 - площадь под импульсом.
- площадь под импульсом.
1.1 Свойства преобразования Фурье
а) Сдвиг сигнала во времени s2 (t)=s1 (t-t0 ).
![]()
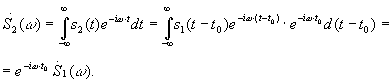
Сдвиг во времени функции s(t) на ±t0 приводит к сдвигу фазы спектра на ±wt0 . Это позволяет для удобства разложения в спектр сдвигать сигнал относительно начала координат.
б) Сжатие и расширение сигнала s2 (t)=s1 (nt) .
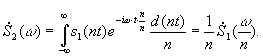
При сжатии сигнала в n раз на временной оси во столько же раз расширяется его спектр на оси частот при уменьшении модуля в n раз. Наоборот, при растяжении сигнала во времени имеет место сужение спектра и увеличение модуля спектральной плотности. Т. о. сжатие спектра импульса с целью повышения точности измерения частоты требует удлинения времени измерения. В то же время сжатие импульса по времени с целью, например, повышения точности измерения времени его появления заставляет расширять полосу пропускания измерительного устройства. В теории преобразования Фурье доказывается, что ![]() где
где ![]()
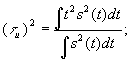
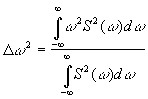 .
.
В реальности это проявление принципа неопределенности: ![]() При
При ![]()
![]() при несреднеквадратичном определении
при несреднеквадратичном определении ![]() и
и ![]() .
.
в) Дифференцирование и интегрирование сигнала
![]()
![]()
![]()
Аналогично спектральная плотность интеграла ![]() равна
равна ![]()
г) Сложение сигналов (линейность преобразования)
![]()
![]() - из-за линейности операции интегрирования.
- из-за линейности операции интегрирования.
д) Спектр произведения двух функций
![]()
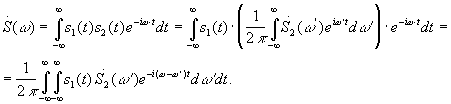
Изменяем порядок интегрирования:
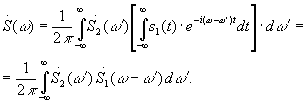
Спектр произведения двух функций равен свертке их спектров (с множителем ![]() ).
).
Аналогично можно показать, что свертке двух функций 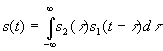 соответствует спектр
соответствует спектр
![]() являющийся произведением исходных спектров.
являющийся произведением исходных спектров.
е) Взаимная обратимость s(t) и
![]() .
.
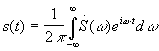 ;
; 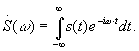
Для четного сигнала s(t)=s(-t),
и в связи с симметричностью пределов интегрирования в выражении для ![]() можно поменять знак в экспоненте
можно поменять знак в экспоненте ![]() Тогда, если по функциональной зависимости
Тогда, если по функциональной зависимости ![]() то
то ![]()
1.2 Распределение энергии в спектре непериодического сигнала
Найдем спектр квадрата функции s(t).
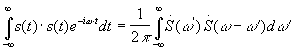 - используем свойства преобразования Фурье для произведения двух функций.
- используем свойства преобразования Фурье для произведения двух функций.
В частном случае (![]() ) будем иметь:
) будем иметь:
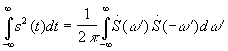 . Переходя от
. Переходя от ![]() к
к ![]() и т. к.
и т. к. ![]() , комплексное сопряжение
, комплексное сопряжение ![]() .
.
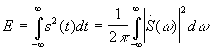 - равенство Парсеваля.
- равенство Парсеваля.
![]() - спектральная плотность энергии (энергия, приходящаяся на единицу полосы частот). Е
- полная энергия сигнала.
- спектральная плотность энергии (энергия, приходящаяся на единицу полосы частот). Е
- полная энергия сигнала.
Для энергии, приходящейся на конечную полосу частот, получим:
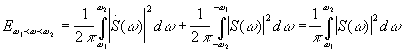 - при симметричной
- при симметричной ![]()
Примеры.Спектр Гауссова (колокольного) импульса
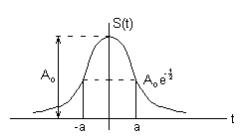 |
![]() , - t
, а
- условная половина длительности на уровне 0,606.
, - t
, а
- условная половина длительности на уровне 0,606.
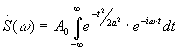 .
.
Произведем преобразование в показателях степени:
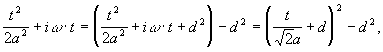
где d - определяется из условия:
![]() откуда
откуда ![]()
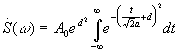 .
.
При d
- конечном 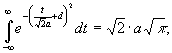 т. к.
т. к. 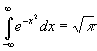 .
.
Тогда 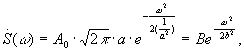 т. е. спектр Гауссова импульса имеет Гауссову форму:
т. е. спектр Гауссова импульса имеет Гауссову форму: ![]()
![]() .
.
Можно показать, что Гауссов импульс обладает наименьшим ![]() при среднеквадратичном их определении.
при среднеквадратичном их определении.
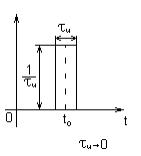
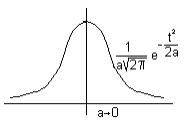
Спектр d-функции
|
 |
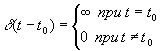 .
.
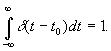
В качестве d -функции может выступать сигнал любой формы с бесконечно малой длительностью и единичной площадью.
1.3 Свойства d-функции
1) 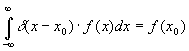 - фильтрующее свойство.
- фильтрующее свойство.
2) Четность ![]()
3) Нормировка ![]()
Спектральная плотность
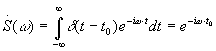 .
.
При t0
= 0,
![]() ,
,
при t0
0,
![]() .
.
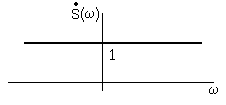 |
![]() - это спектральное определение d
-функции.
- это спектральное определение d
-функции.
Аналогично ![]() - определение d
-функции в частотной области.
- определение d
-функции в частотной области.
Спектральная плотность гармонического колебания
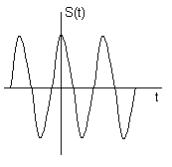 |
Одним из условий применения интегрального преобразования Фурье функции s(t)
является ее абсолютная интегрируемость Применениеd- функции позволяет получить спектральную плотность и для неинтегрируемых функций. |
Пусть ![]() Найдем спектральную плотность, формально не обращая внимания, что сигнал абсолютно не интегрируем.
Найдем спектральную плотность, формально не обращая внимания, что сигнал абсолютно не интегрируем.
Произведем замену ![]() .
.
![]()
Но ![]() тогда
тогда
![]() .
.
Гармоническому колебанию с конечной амплитудой соответствует бесконечно большая спектральная плотность на дискретных частотах ±w0 .
В частности, для постоянного напряжения w0
= 0, ![]()
![]()
Задание 2
В соответствии с номером варианта (последняя цифра в номере списка группы) определить энтропию источника сообщений.
| 4 | 0,15 | 0,01 | 0,09 | 0,25 | 0,01 | 0,04 | 0,1 | 0,18 | 0,02 | 0,15 |
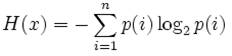
![]()
Задание 3
Для источника сообщений предыдущего задания построить эффективный код Хаффмена.
| x4 | 0,25 | 0,25 | 0,25 | 0,25 | 0,25 | 0,25 | 0, 32 | 0,4 3 | 0,5 7 | 1 |
| x8 | 0,18 | 0,18 | 0,18 | 0,18 | 0,18 | 0,25 | 0,25 | 0,32 | 0,43 | |
| x6 | 0,15 | 0,15 | 0,15 | 0,15 | 0,1 7 | 0,18 | 0,25 | 0,25 | ||
| x9 | 0,15 | 0,15 | 0,15 | 0,15 | 0,15 | 0,17 | 0,18 | |||
| x3 | 0,10 | 0,10 | 0,10 | 0,10 | 0,15 | 0,15 | ||||
| x7 | 0,09 | 0,09 | 0,09 | 0,03 | 0,10 | |||||
| x10 | 0,04 | 0,04 | 0,04 | 0, 08 | ||||||
| x1 | 0,02 | 0,02 | 0,0 4 | |||||||
| x2 | 0,01 | 0,0 2 | ||||||||
| x5 | 0,01 |
![]()
![]()
|
|
|
|
|
|
|

![]() x2-1110001
x2-1110001
![]() x3-1111
x3-1111
![]()
![]()
|
x5-1110000
![]()
![]() x6-11101
x6-11101
x7-010
|

|
|
![]() x9-111001
x9-111001
![]()
![]()
|
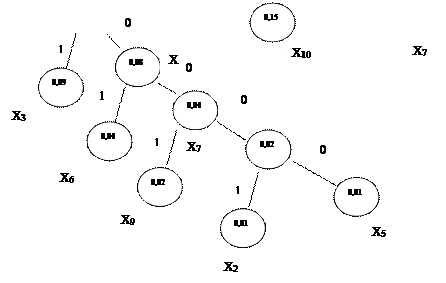 |
Задание 4
Построить двоичный групповой помехоустойчивый код Хэмминга для исправления одиночных ошибок. Количество передаваемых сообщений – 45.
Дать описание построенного кода в виде проверочных равенств и матрицы.
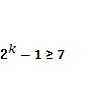
k=3
![]()
m=3
n=m+k
n=6
(6,3)
Исходный код:
k1 k2 k3
Код Хэмминга:
m1m2k1m3k2k3
a1 a2 a3 a4 a5 a6
Варианты разрядов в которых может возникнуть ошибка
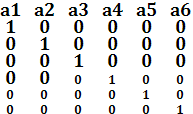
Номера разрядов в которых может возникнуть ошибка
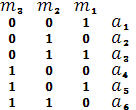
![]()
![]()
![]()
Значения проверочных битов
![]()
![]()
![]()
Проверочные равенства:
![]()
![]()
![]()
![]() – проверочный синдром, указывающий номер бита с ошибкой
– проверочный синдром, указывающий номер бита с ошибкой
Проверочная матрица:
![]()
Пример:
Закодируем сообщение 101
Исходный код
![]()
Закодированный код
![]()
Найдем проверочные разряды
![]()
![]()
![]()
Получаем код
![]()
Смоделируем ошибку при передаче сообщения. Инвертируем 5 бит сообщения 101101 и получим 10111 1.
Представим принятый код в виде
![]()
Используя проверочные равенства найдем
![]()
![]()
![]()
Получаем проверочный синдром S(101), который указывает на ошибку в 5 бите. Для исправления ошибки необходимо проинвертировать указанный бит 10110 1. В результате получаем исходный закодированный код. Для его декодирования необходимо исключить из сообщения биты 1,2, и 4 биты. Получаем исходный код 101.
Литература
1. Блейтхут Р. Для теории и практики кодов, контролирующих ошибки. / Под общей редакцией К. Ш. Зигангирова . -г. Москва.: Мир, 2003.
2. Дмитриев В.И. Прикладная теория информации. – М.: Высшая школа, 1989.
3. Мсхаля Ж. Основы современных информационных технологий. Учебное пособие для вузов. М.: АСВ, 2003.
4. Методические указания к лабораторным работам по курсу Элементы теории информации для студентов специальности Программное обеспечение вычислительной техники и автоматизированных систем / Составители: В.Н. Ярмолик, А.В. Литвиненко, А.И. Янушкевич. – Мн.: БГУИР, 1996.