Стальной каркас одноэтажного промышленного здания
СОДЕРЖАНИЕ: Характеристики мостового крана. Компоновка конструктивной схемы здания. Проектирование подкрановых конструкций. Расчет поперечной рамы каркаса, ступенчатой колонны, стропильной фермы: сбор нагрузок, характеристика материалов и критерии их выбора.Курсовой проект
На тему:
«Стальной каркас одноэтажного промышленного здания»
1. Исходные данные
1.1 Данные для проектирования
Место строительства: г. Самара;
Наименование цеха: цех сборочный;
Тип здания: отапливаемое;
Пролет L= 18 м;
Длина l= 96 м;
Высота отметки головки подкранового рельса: Н1 =14,4 м;
Грузоподъемность крана: Q=1000 кН;
Сталь подкрановых конструкций: С345;
Группа режимов работы кранов: 3К;
Вид сечения элементов фермы: ШТ.;
Сталь фермы: С255;
Вид кровли: без прогонов;
Сталь колонны: С245.
1.2 Характеристики мостового крана
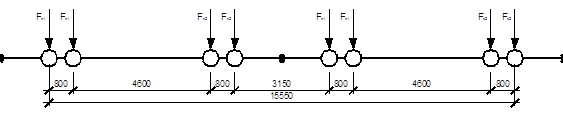
Рис. 1. Мостовой кран Q=100 т
Для кранов с грузоподъемностью
100 т. при пролете здания 18 м: Нк =3700 мм;
В1 =400 мм;
В2 =9350 мм;
К=4600 мм.
Максимальное давление на колеса: Fn1 =410 кН;
Fn2 =450 кН;
Вес тележки: Gт =410 кН;
Вес крана с тележкой: Gк = 1250 кН;
Тип кранового рельса: КР-120;
Высота рельса: hр =170 мм;
Высота подкрановой балки: hб =1500 мм.
2. Компоновка конструктивной схемы здания
2.1 Разбивка сетки колонн
Согласно требованиям унификации, шаг колонн однопролетных зданий принимают равным 6 или 12 м. Это определяется сравнением параметров. Опыт показывает, что для зданий пролетом 30 и более м. и с высотой 14 и более м., с кранами грузоподъемностью более 50–75 т. экономичнее оказывается шаг 12 м. Принимаем шаг колонн равным 12 м. Колонны у торцов здания смещаем с модульной сетки внутрь на 500 мм. для удобства оформления углов стандартными ограждающими элементами. Для здания данной протяженности (96 м.) и категории (отапливаемое) температурный шов не требуется.
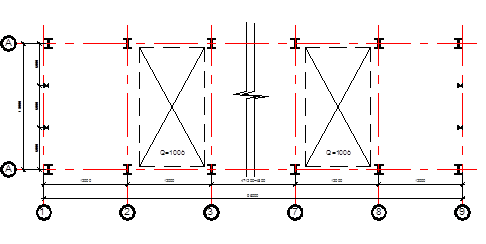
Рис. 2. Разбивка сетки колонн
2.2 Компоновка поперечной рамы здания
Компоновку поперечной рамы начинают с установления основных (габаритных) размеров элементов конструкций в плоскости рамы. Размеры по вертикали привязывают к отметке уровня пола, принимая ее нулевой. Размеры по горизонтали привязывают к продольным осям здания. Все размеры принимают в соответствии с основными положениями по унификации. Сначала целесообразно установить вертикальные размеры.
Вертикальные габариты здания зависят от технологических условий производства. Они определяются расстоянием от уровня пола до головки кранового рельса Н1 =14,4 м и расстоянием от головки кранового рельса до низа несущих конструкций покрытия Н2 . В сумме размеры Н1 и Н2 определяют полезную высоту цеха H0 .
Размер Н2 диктуется высотой мостового крана:
,
где HK + 100 мм – габаритный размер от головки рельса до верхней точки тележки крана (3700 мм, см. стр. 530 [2]) плюс установленный по требованиям техники безопасности зазор между этой точкой и строительной конструкциями, равный 100 мм;
f – размер, учитывающий прогиб конструкции покрытия (ферм, связей), принимаемый равным 200400 мм, в зависимости от величины пролета.
В нашем случае L= 18 м, принимаем f = 200 мм;
Тогда Н2 = (3700 мм + 100 мм) + 200 мм = 4000 мм.
Далее устанавливаем высоту цеха от уровня пола до низа стропильных ферм:
Н0 =14400 мм + 4000 мм=18400 мм;
В соответствии с «Основными положениями по унификации» высоту цеха от уровня пола до низа стропильных ферм Н принимаем до высоты 10,8 м кратной 1,2 м, а при большей высоте кратно 1,8 м: Н0 = 19,8 м.
Уточняем размер H1 : H1 =H0 – H2 =19,8 – 4,0 = 15,8 м.
Высота верхней части колонны HB :
где hб – высота подкрановой балки, которая предварительно принимается 1/81/10 пролета балки;
hр
– высота кранового рельса – 170 мм. Принимаем 
.
HB =1500 мм + 170 мм + 4000 мм = 5670 мм
Размер нижней части колонны:
где Нзагл = (6001000) мм – обычно принимаемое заглубление опорной плиты башмака колонны ниже нулевой отметки пола.
Hн =19800 мм – 5670 мм + 800 мм = 14930 мм;
Общая высота колонны рамы:
H = 5670 мм + 14930 мм =20600 мм;
Высота фермы зависит от принятой конструкции стропильных ферм и принимается hоп =2250 мм – для ферм пролетом 18 и 24 метров.
Исходя их того, что в здании используется мостовой кран Q = 100 т и группа режимов работы кранов 3К принимается привязка наружной грани колонны а = 500 мм. Принимаем высоту верхней части ступенчатой колонны hВ = 700 мм (исходя из того, что привязка а = 500 мм), что удовлетворяет условию:
При назначении высоты нижней части ступенчатой колонны необходимо учесть, что для того чтобы кран при движении вдоль цеха не задевал колонну, расстояние от оси подкрановой балки до оси колонны должно быть не менее:
;
где B1 = 400 мм;
l1 =400 мм + (700 мм – 500 мм) + 75 мм = 675 мм.
Принимаем l1 =750 мм (кратно 250 мм).
Ось подкрановой ветви колонны обычно совмещают с осью подкрановой балки, тогда должно выполняться условие:
hн = 750 мм + 500 мм=1250 мм;
Высота нижней части составной колонны должна удовлетворять условию:
Пролет мостового крана: 
2.3 Выбор схемы связей
Вертикальные связи между колоннами каркаса в продольном направлении обеспечивают жесткость и неизменяемость каркаса здания в продольном направлении от воздействия продольных нагрузок; ветровых – на торцевые стены здания и тормозных сил от мостовых кранов. Также эти связи служат для обеспечения устойчивости колонн.
Рис. 3. Связи по колоннам
Связи нижнего яруса следует располагать ближе к середине здания или температурного блока для того, чтобы обеспечить свободу температурных деформаций продольных элементов и избежать дополнительных температурных напряжений, которые могут быть весьма значительны и ведут к повреждению конструкций.
Верхние вертикальные связи ставят в тех же осях, что и нижние. Иногда для повышения жесткости каркаса верхние связи 2 ставят в торцах здания или температурного блока, т. к. небольшая жесткость надкрановой части колонн незначительно влияет на температурные напряжения. В пределах высоты стропильных ферм в связевом блоке и по торцам здания ставят связи 3, которые идут на монтаж в виде готовой связевой фермы. В остальных местах колонны соединяются распорками.
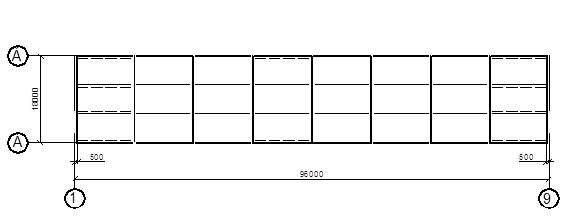
Рис. 4. Связи по верхнему поясу ферм
Связи между фермами, создавая общую пространственную жесткость каркаса, обеспечивают:
· устойчивость сжатых элементов ригеля из плоскости ферм;
· перераспределение местных нагрузок (например, крановых), приложенных к одной из рам, на соседние рамы;
· удобство монтажа;
· заданную геометрию каркаса;
· восприятие и передачу на колонны некоторых нагрузок.
Рис. 5. Связи по нижнему поясу ферм
Система связей покрытия состоит из горизонтальных и вертикальных связей.
2.4 Компоновка фасада. Выбор элементов ограждения
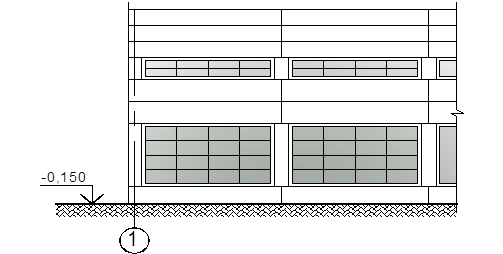
Рис. 6. Компоновка фасада
В качестве ограждающих конструкций выбираем типовые плиты длиной 12 м вдоль длиной части фасада, длиной 6 м вдоль короткой части фасада. Плиты продольной части фасада крепятся на колонны. Плиты поперечной части фасада крепятся на фахверковые колонны двутаврового профиля.
3. Проектирование подкрановых конструкций
3.1 Определение расчетных усилий
Рассмотрим различные варианты положения крана на подкрановой балке для определения наиболее невыгодного загружения:
Рис. 7. Варианты загружения подкрановой балки
Заметим, что некоторые варианты симметричны друг другу, будем рассматривать вариант №3.
Для крана грузоподъемностью Q=100 т принимаем данные для расчета:
Расчетное вертикальное давление колес крана:
где n =0,95 – коэффициент надежности по назначению;
f =1,1 – коэффициент надежности по нагрузки;
=0,85 (при учете 2-х кранов группы режима работы 3К) – коэффициент сочетания;
kF =1,0 (при шаге колонн 12 м и группе режима работы 3К) – коэффициент динамичности;
Fn1 = 410 кН; Fn2 = 450 кН – нормативное вертикальное давление колеса крана (см. стр. 530 [2]);
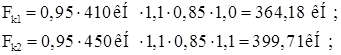
Равнодействующая вертикальных расчетных давлений колес:
Плечо равнодействующей силы:
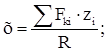
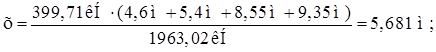
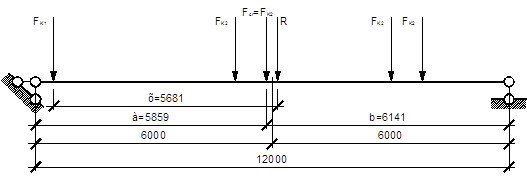
Рис. 8. Расчетная схема загружения подкрановой балки
Установка будет расчетной, если ближайшее к равнодействующей колесо будет являться критическим грузом:
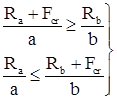
где a, b – расстояние от опор до критического груза;
Fcr – проверяемый критический груз;
Ra = 364,18 кН + 399,71 кН = 763,89 кН – равнодействующая всех грузов, расположенных слева от критического;
Rb = 2·399,71 кН = 799,42 кН – равнодействующая всех грузов, расположенных справа от критического.
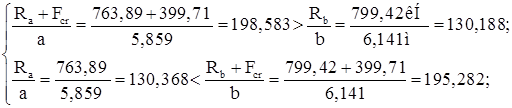
Условие выполняется, следовательно, принятая схема загружения является расчетной.
Определяем ординату линии влияния изгибающего момента для сечения под критическим грузом:
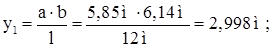
Далее строим линию влияния изгибающих моментов, и остальные ординаты получаем графически.
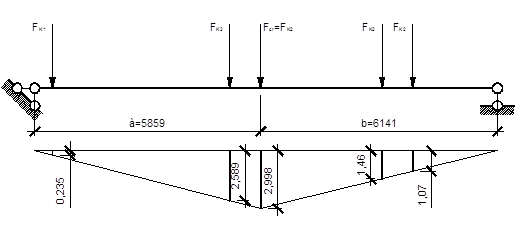
Рис. 9. Линия влияния изгибающего момента
Расчетный изгибающий момент от вертикальной нагрузки:
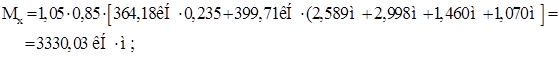
Расчетный изгибающий момент от горизонтальной нагрузки:
Здесь 
– расчетное горизонтальное давление колес крана;
Нормативное горизонтальное давление колес крана:
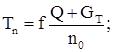
где Q = 1000 кН – грузоподъемность крана;
GТ = 410 кН – вес тележки крана;
n0 = 4 – число колес крана по одну сторону;
f = 0,05 (для кранов с гибким подвесом) – коэффициент трения.
Расчетное горизонтальное давление колес крана:
Наибольшая поперечная сила Qmax в разрезной балке будет при таком положении нагрузки, когда одна из сил находится непосредственно у опоры, а остальные расположены как можно ближе к этой же опоре.
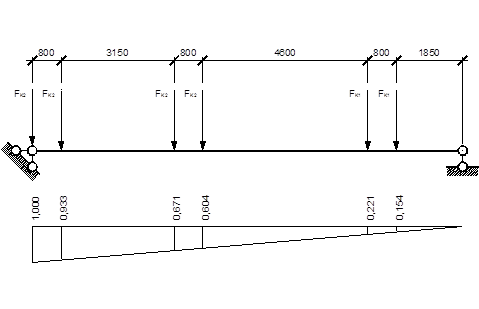
Рис. 10. Линия влияния поперечной перерезывающей силы
Максимальная поперечная перерезывающая сила от вертикальных нагрузок:
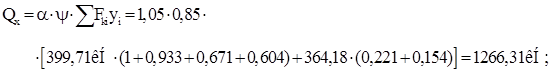
где a = 1,05 (для балки l = 12 м) – коэффициент, учитывающий вес подкрановой балки и полезную нагрузку от тормозной балки.
3.2 Подбор сечения подкрановых конструкций
Вначале подберем сечение подкрановой балки. Требуемый момент сопротивления сечения подкрановой балки:
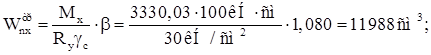
где b – коэффициент, учитывающий изгиб конструкции в 2-х плоскостях;
с = 1 – коэффициент условий работы конструкции;
Ry = 30 кН/см2 – для стали С345, для листового широкополосного универсального проката толщиной 2040 мм.
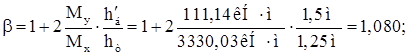
где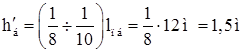 
– предварительная высота подкрановой балки;
hT = 1250 мм – ширина тормозной конструкции, предварительно принимается равной ширине нижней части колонны hн .
Минимальная высота подкрановой балки:
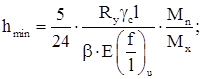
Е= 2,06·105 МПа – модуль упругости прокатной стали;
l = 12 м – длина подкрановой балки;
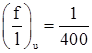(для кранов группы режима 3К) – предельный относительный прогиб подкрановой балки;
Мn – нормативный изгибающий момент от загружения балки одним краном. Определяем Мn аналогично Мх :
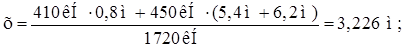
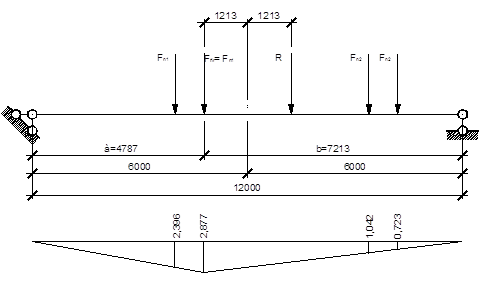
Рис. 11. Расчетная схема загружения подкрановой балки нормативной вертикальной нагрузкой
Определяем ординату линии влияния изгибающего момента для сечения под критическим грузом:
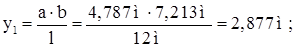
Далее строим линию влияния изгибающих моментов, и остальные ординаты получаем графически.
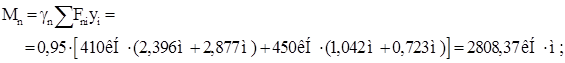
Минимальная высота подкрановой балки:
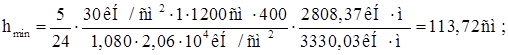
Оптимальная высота подкрановой балки:
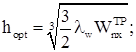
где lw = 120 – гибкость стенки (принята предварительно).
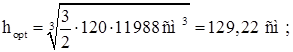принимаем высоту подкрановой балки h = 130 см, что больше hmin
= 95,63 см.
Определяем толщину стенки подкрановой балки из 2-х условий:
1) Условие на срез:
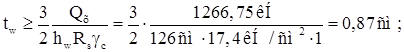
где Rs = 0,58Ry = 0,58·30 кН/см2 = 17,4 кН/см2 ;
hw = h – 2tf =130 см - 2.2 см = 126 см – высота стенки подкрановой балки;
tf = 2 см – толщина поясов подкрановой балки (принята предварительно).
2) Условие местной устойчивости без продольных ребер:
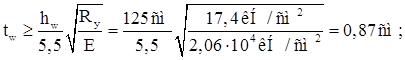
Принимаем толщину стенки подкрановой балки tw =1 cм.
Требуемый момент инерции подкрановой балки:
Проектируем пояса подкрановой балки.
Требуемый момент инерции двух поясов подкрановой балки:
Требуемая площадь пояса подкрановой балки:
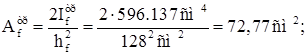
hf = 130cм - 2 см = 128cм.
Принимаем толщину пояса подкрановой балки tf = 2 см.
Тогда, требуемая ширина пояса подкрановой балки:
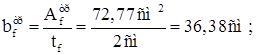
Принимаем ширину поясов подкрановой балки bf = 40 см.
Проверка условия местной устойчивости сжатого пояса:
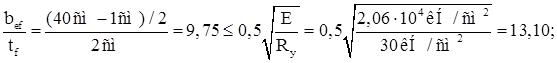
Условие выполняется.
Производим компоновку всего сечения подкрановой конструкции с учетом тормозной балки и определяем положение центра тяжести подкрановой конструкции.
Принимаем тормозную балку из швеллера №30 и рифленого листа толщиной tрл = 8 мм.
Ширина рифленого листа:
В нормах принято, что вертикальные нагрузки воспринимает только подкрановая балка, поэтому ось Х будет проходить через центр тяжести подкрановой балки. Если подкрановая балка симметричная, то ось Х проходит посередине. Горизонтальные нагрузки воспринимает только тормозная балка, которая состоит из трех элементов: верхнего пояса, рифленого листа и поддерживающего швеллера. Ось У будет проходить через центр тяжести тормозной балки.
Находим центр тяжести подкрановой конструкции:
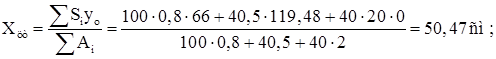
Рис. 12. Компоновка поперечного сечения подкрановой конструкции
Определим геометрические характеристики скомпонованного сечения. Относительно оси Х определяем только характеристики подкрановой балки.
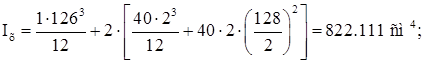
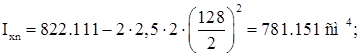
Относительно оси Y определяем характеристики тормозной балки:
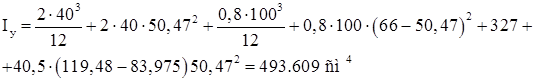
3.3 Проверка прочности и жесткости подкрановых конструкций
Рис. 13. Эпюра нормальных напряжений в подкрановой конструкции
Верхний пояс работает одновременно на изгиб в вертикальной и горизонтальной плоскости, поэтому прочность в т. А по нормальным напряжениям:
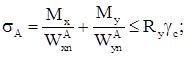
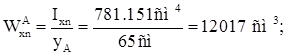
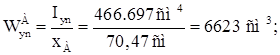
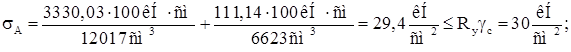
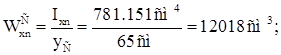
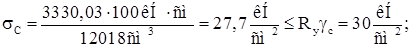
Далее проверяем наружный пояс тормозной балки в точке В.
Тормозная балка воспринимает следующие нагрузки:
1) Временная полезная нагрузка:
где gf = 1,2 – коэффициент надежности по нагрузке;
P0n =2 кН/м2 – нормативная временная нагрузка, задаваемая технологами.
2) Нагрузка от собственного веса настила:
3) Нагрузка от собственного веса швеллера:
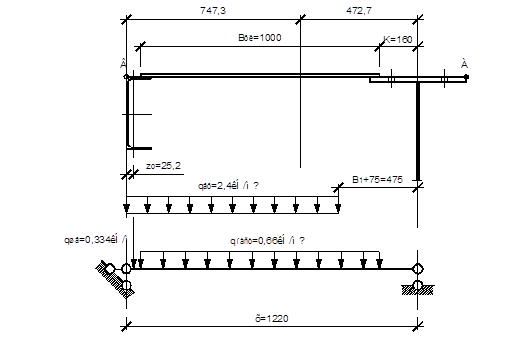
Рис. 14. Вертикальные нагрузки на тормозную балку
Расчетную нагрузку на швеллер определяем как реакцию на левую опору условной расчетной схемы:
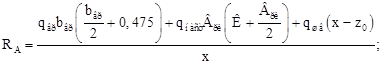
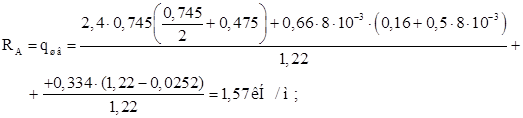
Определим изгибающий момент в швеллере:
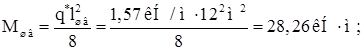
Проверим прочность швеллера по нормальным напряжениям в точке В:
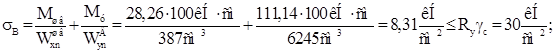
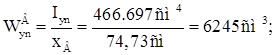
Проверим жесткость швеллера (по нормативным нагрузкам):
Здесь 
Проверим прочность подкрановой балки на опоре по касательным напряжениям:
Здесь 
– статический момент полусечения балки.
Проверим прочность стенки подкрановой балки по местным напряжениям от давления колес крана:
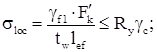
где gf1 =1,1 (для группы режима кранов 3К) – дополнительный коэффициент надежности по нагрузке;
Fk – расчетное вертикальное давление колеса крана без учета коэффициента динамичности;
где gn = 0,95 – коэффициент надежности по назначению;
gf = 1,1 – коэффициент надежности по нагрузке;
Fn max = 450 кН – нормативное вертикальное давление колеса крана.
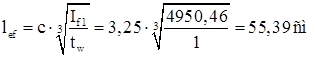– условная длина распределения местного давления колес крана.
где с=3,25 – коэффициент для сварных балок;
If1 – сумма собственных моментов инерций верхнего пояса балки и кранового рельса:
здесь Iр = 4923,79 см4 – момент инерции кранового рельса КР-120 (ГОСТ 4121–76).
– условие выполняется.
Проверка жесткости подкрановой балки от действия одного крана:
где Мn = 280837,1 кН.см – нормативный изгибающий момент от загружения балки одним краном.
– для режимов работы 1К6К.
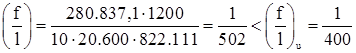– условие выполняется.
3.4 Проверка общей устойчивости подкрановой балки
При наличии тормозной балки считается, что общая устойчивость обеспечена и проверка не требуется.
3.5 Проверка местной устойчивости элементов подкрановой балки
Устойчивость верхнего сжатого пояса подкрановой балки будет обеспечена, если выполняется условие:
Для проверки устойчивости стенки определим ее условную гибкость:
2,2 – требуется укрепить стенку поперечными ребрами жесткости.
Принимаем ширину поперечных ребер 
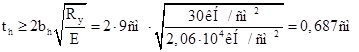– принимаем толщину tr
=8 мм. Ребра приваривают только к стенке подкрановой балки швами с минимальным конструктивным катетом. К верхнему и нижнему поясу ребра не привариваются.
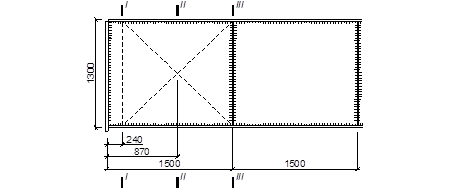
Рис. 15. К расчету на местную устойчивость
По длине балки ребра ставятся по аналогии с типовыми проектами с шагом 1,5 м.
Рис. 16. Схема загружения расчетного отсека
Каждый отсек стенки подкрановой балки проверяется на местную устойчивость по формуле:
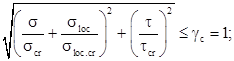
Находим расчетные отсеки:
Опорная реакция:
Находим средние значения поперечной силы и изгибающего момента:
Здесь 
– коэффициент, учитывающий собственный вес конструкций при пролете 12 м.
Находим нормальные и касательные напряжения:
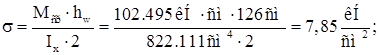
Коэффициент 
:
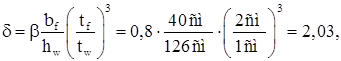
где 
=0,8.
Т.к. 
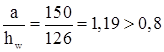и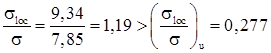 
,
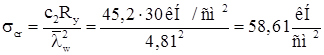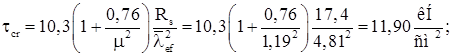
где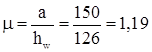 
– отношение большей стороны пластинки (отсека) к меньшей;
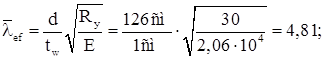
где d=hw =126 см – меньшая из сторон отсека.
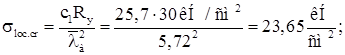
Здесь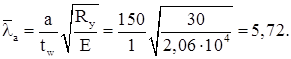 
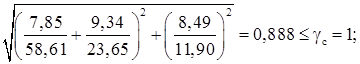
Местная устойчивость сжатого пояса и стенки балки обеспечена.
3.6 Расчет поясных швов
Поясные швы, которыми верхний пояс крепится к стенке, воспринимают одновременно сдвигающие усилия от изгиба балки и сосредоточенные усилия от давления колес крана. Сварка – автомат под слоем флюса. Проволока Св-10НМА. Rwf
= 240 МПа; 
- коэффициенты, учитывающие глубину провара; 
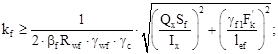
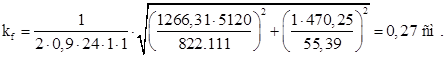
По конструктивным соображениям принимаем kf = 6 мм.
Нижний пояс воспринимает усилие сдвига:
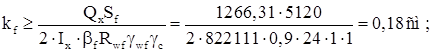
По конструктивным соображениям принимаем kf = 6 мм.
3.7 Проектирование опорного ребра подкрановой балки
При шарнирном соединении опорная реакция передается с балки на колонну через опорные ребра, которые ставятся в торце балки. Опорные ребра надежно прикрепляют к стенке балки сварными угловыми швами, а торцы строгают.
Размеры опорных ребер находятся из расчета на смятие их торцевой поверхности опорной реакцией балки V:
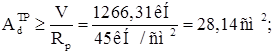
где V=Qх = 1266,31 кН;
Rp = Ru = 450 МПа расчетное сопротивление стали смятию торцевой поверхности.
Задаемся шириной опорного ребра bd = 40 см. Тогда толщина опорного ребра:
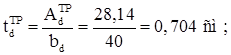
Условие местной устойчивости:
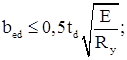
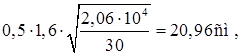здесь предварительно задаемся td
=1,6 см.
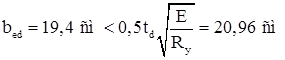– условие выполняется принимаем толщину опорного ребра td
= 16 мм.
Тогда фактическая площадь смятия будет равна:
Выступающая вниз часть опорного ребра не должна превышать a = 1,5td =1,5.1,6 см = 2,4 см, принимаем a = 2 см.
Вследствие недостаточных размеров ребер опорный участок балки может потерять устойчивость из плоскости балки, поэтому его рассчитывают на продольный изгиб как стойку с расчетной длиной равной высоте стенки. В площадь сечения условного стержня длиной As включаются опорные ребра и примыкающие участки стенки шириной s:
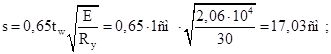
Устойчивость опорного участка балки относительно оси Z проверяют по формуле:
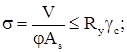
где 
– площадь сечения условного стержня;
– коэффициент продольного изгиба стойки, в зависимости от гибкости 
,
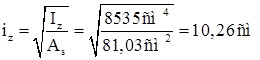, здесь:
– момент инерции условного стержня относительно оси Z;
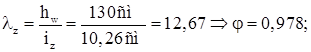
– устойчивость опорного участка обеспечена.
4. Расчет поперечной рамы каркаса
4.1 Расчетная схема рамы
Фактическая высота подкрановой балки отличается от принятой первоначально при компоновке рамы, уточним размеры Нв и Нн :
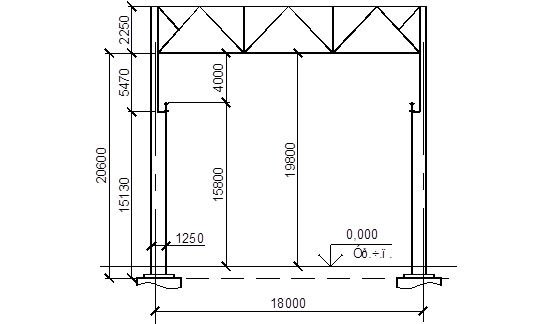
Рис. 17. Конструктивная схема рамы
Конструктивную схему рамы приводим к расчетной схеме, соблюдая следующее:
оси колонн проходят через центры тяжестей сечений;
заделка колонн принимается на уровне низа башмака;
ригель проходит по оси нижнего пояса фермы и принимается горизонтальным, т.к. уклон фермы менее 1/8.
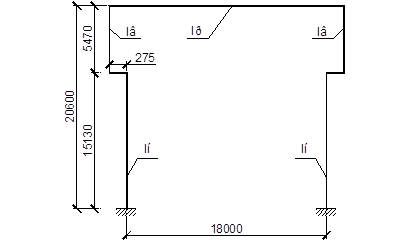
Рис. 18. Расчетная схема рамы
Расстояние между центрами тяжести верхнего и нижнего участков колонн: 
4.2 Сбор нагрузок на поперечную раму
| Состав кровли | Нормативная нагрузка, кН/м2 | Коэффициент надежности по нагрузке  |
Расчетная нагрузка, кН/м2 |
| Защитный слой гравия 15 мм. | 0,3 | 1,3 | 0,39 |
Гидроизоляция: 4 слоя рубероида |
0,2 | 1,3 | 0,26 |
| Цементная стяжка 20 мм | 0,4 | 1,3 | 0,52 |
Пенопласт  100 мм |
0,05 | 1,2 | 0,06 |
| Пароизоляция: 1 слой фольгоизола | 0,05 | 1,3 | 0,07 |
| Ж/б ребристая плита 300 мм | 2,7 | 1,1 | 2,97 |
| Стропильные фермы и связи покрытия | 0,35 | 1,05 | 0,37 |
| Итого: | 4,05 | 4,64 |
Определим постоянную равномерно распределенную нагрузку:
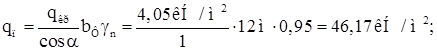
где bф = 12 м – шаг ферм;
– коэффициент надежности по назначению.
Опорная реакция ригеля рамы:
Рис. 19. Схема приложения постоянных нагрузок
В F1 , F2 входят: вес верхнего и нижнего участков колонны, а также собственный вес стенового ограждения с переплетами, прикрепленными к этим участкам.
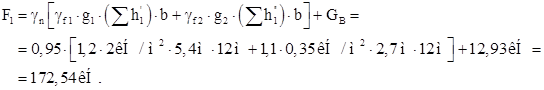
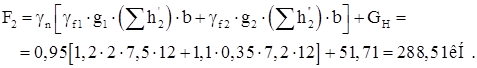
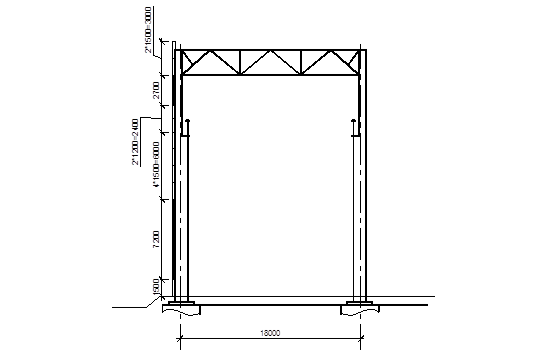
Рис. 20. Схема установки стеновых и оконных панелей.
Здесь:
– коэффициент надежности по назначению;
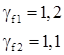– коэффициенты надежности по нагрузке;
g1 =2 кН/м2 – поверхностная масса навесных стен;
g2 =0,35 кН/м2 – поверхностная масса оконных переплетов с остеклением;
b=12 м – ширина грузовой площади стен;
– суммарная высота стеновых панелей, нагрузка с которых передается на верхнюю часть колонны;
– суммарная высота оконных переплетов, нагрузка с которых передается на верхнюю часть колонны;
– суммарная высота стеновых панелей, нагрузка с которых передается на нижнюю часть колонны;
– суммарная высота оконных переплетов, нагрузка с которых передается на нижнюю часть колонны;
GB =0,2GК – расчетная нагрузка от веса верхней части колонны;
GH =0,8GК – расчетная нагрузка от веса нижней части колонны;
GК – вес всей колонны.
,
gкол =0,6 кН/м2 – средний расход стали на колонны каркаса в расчете на 1 м2 площади здания;
Расчетная линейная нагрузка на ригель рамы определяется:
,
– коэффициент перехода от веса снегового покрова земли к снеговой нагрузке на покрытие (прил. 3 СНиП «Нагрузки и воздействия»);
Sg =2,4 кПа – расчетное значение веса снегового покрова на 1 м2 поверхности земли (IV снеговой район).
Рис. 21. Снеговая нагрузка
Опорная реакция ригеля рамы:
Вертикальная нагрузка на колонну от двух сближенных кранов наибольшей определяется с коэффициентом сочетания 
(режим работы 3К).
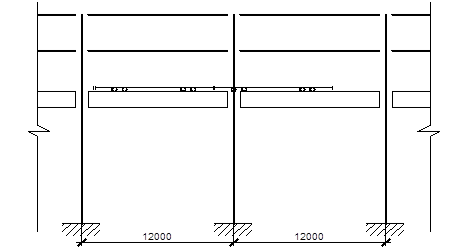
Рис. 22. Вид на каркас сбоку
Рис. 23. Линия влияния опорных реакций подкрановых балок
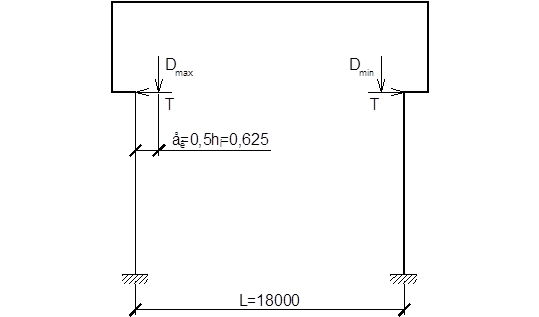
Рис. 24. Крановые нагрузки
Определяем расчетные давления на колонну Dmax (колонна рядом с тележкой), Dmin (противоположная от тележки колонна).
,
Где:
Fk i – расчетное давление колеса крана;
Fni – нормативное давление колеса крана с противоположной стороны;
yi – ординаты линии влияния;
– нормативный вес подкрановых конструкций;
– коэффициенты надежности по нагрузке;
P0 n = 2 кН/м2 – полезная нормативная нагрузка на тормозную балку;
b=12 м – шаг колонн;
bT =1 м – ширина тормозной конструкции.
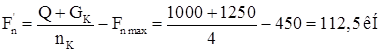– нормативное давление колес крана с противоположной от тележки стороны;
где Q= 1000 кН – грузоподъемность крана;
Fnmax =450 кН – максимальное нормативное давление колеса крана;
GK = 1250 кН – масса крана с тележкой;
nK =4 – число колес с одной стороны одного крана.
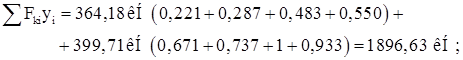
Расчетная горизонтальная сила Т, передаваемая на колонну, определяется:
где 
кН – нормативное значение горизонтального давления колеса мостового крана.
Изгибающие моменты, возникающие по оси колонны от сил Dmax , Dmin равны:
Расчетная ветровая нагрузка в любой точке по высоте рамы будет равна:
с наветренной стороны:
с подветренной стороны:
,
где 
– коэффициент надежности по нагрузке;
W0 =0,38 кПа – нормативный скоростной напор в зависимости от ветрового района (III ветровой район);
се =0,8; се3 =0,6 – аэродинамические коэффициенты (по прил. 4 СНиП «Нагрузки и воздействия»;
k – коэффициент, учитывающий изменение ветрового давления по высоте.
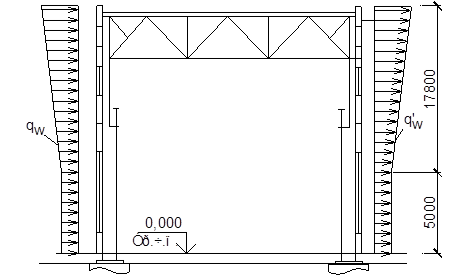
Рис. 25. Схема изменения ветровой нагрузки по высоте
В=12 м – шаг колонн.
Тип местности – В.
Тогда ветровая нагрузка на высоте 10, 19,8 и 22,8 м равна:
Для удобства расчета фактическую линейную нагрузку заменяют эквивалентной, равномерно распределенной по высоте колонны.
Рис. 26. Ветровые нагрузки
Приближенно можно определить:
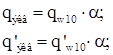
где 
– коэффициент, зависящий от высоты здания.
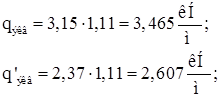
Ветровая нагрузка, которая действует на участке h от низа ригеля до наиболее высокой точки здания, заменяется сосредоточенной силой, приложенной в уровне низа ригеля.
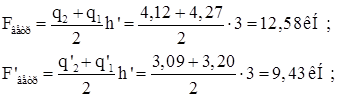
4.3 Определение расчетных усилий в сечениях рамы
Постоянная нагрузка.
Примем условно соотношение между моментами инерции нижней части колонны Iн , верхней части колонны Iв , и моментом инерции ригеля Iр .
, 
;
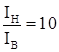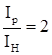Условно принимаем IВ =1.
Вычисляем параметры рамы: 
, 
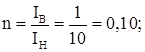
Сосредоточенный момент из-за смещения осей участков колонн 
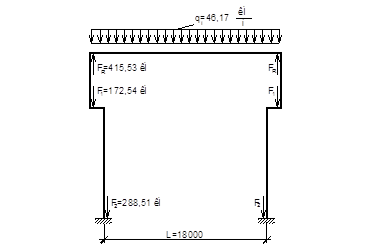
Рис. 27. Схема нагрузки рамы.
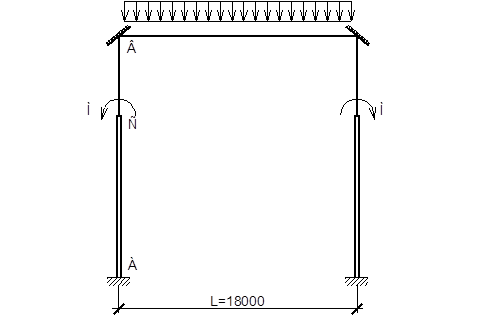
Рис. 28. Основная система метода перемещений
Каноническое уравнение для левого узла:
Узлам ненагруженной рамы дается смещение на угол = 1 и строится эпюра М на растянутых волокнах:
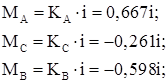
где 
;
КА = 0,667, КС = – 0,261, КВ = – 0,598 – коэффициенты для определения изгибающих моментов, определяемые по таблице 12.4 [2] в зависимости от параметров n и .
Момент в ригеле: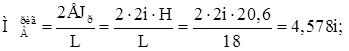 
Моменты от нагрузки на стойках (рис. 29, в):
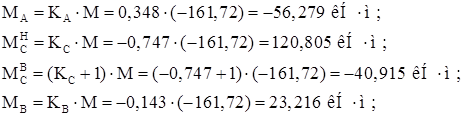
Моменты на опорах ригеля определяются как в защемленной балке:
Определяем коэффициенты канонического уравнения из условия равновесия узлов:
Угол поворота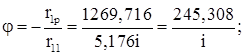 
Строим эпюру моментов от постоянной нагрузки (рис. 29, г):
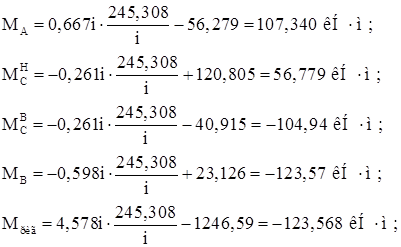
Строим эпюру Q (рис. 29, д):
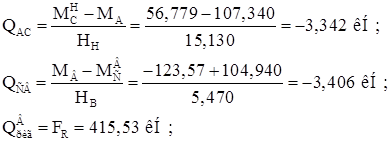
Строим эпюру N (рис. 29, е):
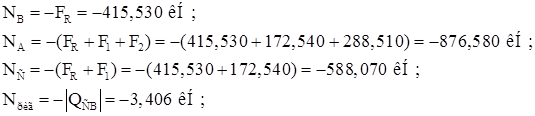
Рис. 29. К расчету рамы на постоянную нагрузку: а – основная система; б – эпюра М1 ; в-эпюра Мр ; г – эпюра М; д – эпюра Q; е – эпюра N
Снеговая нагрузка:
Находим сосредоточенный момент:
Каноническое уравнение:
Моменты от нагрузки на стойках:
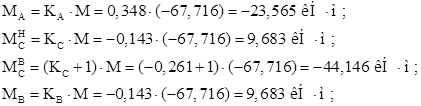
Моменты на опорах ригеля определяются как в защемленной балке:
Определяем коэффициенты канонического уравнения:
;
Угол поворота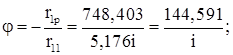 
Строим эпюру моментов от постоянной нагрузки:
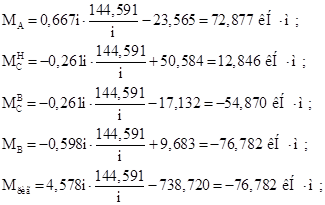
Строим эпюру Q:
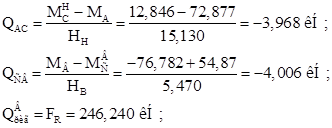
Строим эпюру N:
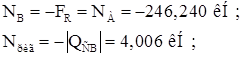
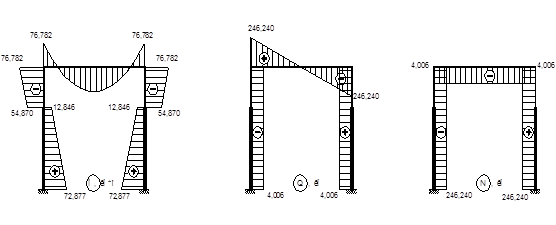
Рис. 30. Эпюры M, Q, N от действия снеговой нагрузки
Вертикальная нагрузка от мостового крана
Расчет проводится при расположении тележки крана у левой стойки.
Проверка возможности считать ригель абсолютно жестким:
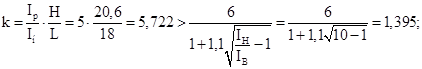
Каноническое уравнение для определения смещения плоской рамы:
Раме дают единичное смещение на D=1 и определяют моменты и реакции от этого смещения:
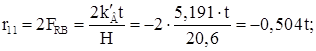
Моменты и реакции на левой стойке от нагрузки:
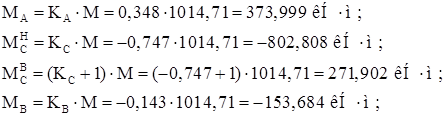
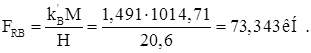
Усилия на правой стойке можно получить аналогично или умножая усилия левой стойки на отношение: 
Реакция верхних концов стоек:
Смещение плоской рамы:
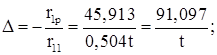
Крановая нагрузка – местная, поэтому aпр 1:
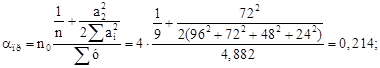
Смещение с учетом пространственной работы
Строим эпюры:
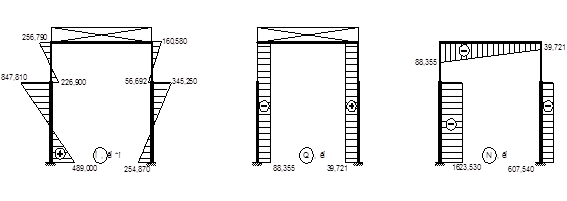
Рис. 31. Эпюры M, Q, N от действия вертикальной крановой нагрузки
Горизонтальная нагрузка от мостового крана
Основная система, эпюра М1 , каноническое уравнение, коэффициент aпр – такие же, как и при расчете на вертикальную нагрузку от мостовых кранов.
Моменты и реакции на левой стойке от нагрузки:
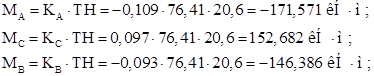
Смещение верхних концов с учетом пространственной работы
Используя те же формулы, строим эпюры:
Рис. 32. Эпюры M, Q, N от действия горизонтальной крановой нагрузки
Ветровая нагрузка
Основная система и эпюра М1 – как для крановых воздействий.
Моменты и реакции на левой стойке от нагрузки:
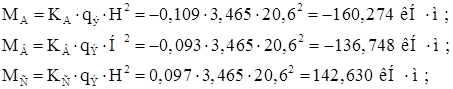
На правой стойке усилия получаются умножением на коэффициент
Коэффициенты канонического уравнения:
Смещение рамы (ветровая нагрузка воздействует на всю раму, поэтому aпр =1)
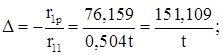
Эпюра Q на левой стойке:
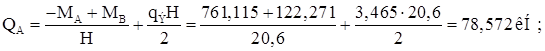
Эпюра Q на правой стойке:
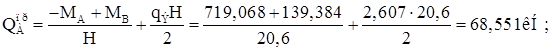
При правильном решении сумма поперечных сил внизу должна быть равна сумме всех горизонтальных нагрузок:
Строим эпюры:
Рис. 33. Эпюры M, Q, N от действия ветровой нагрузки
5. Расчет ступенчатой колонны
Расчетные длины верхней и нижней частей колонны:
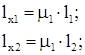
где l1 =HН =15,130 м – длина нижнего участка колонны;
l2 =HB =5,470 м – длина верхнего участка колонны;
– коэффициенты расчетной длины нижнего и верхнего участков колонны.
Т.к. условия 
и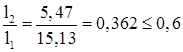 
соблюдается, то коэффициенты определяется по табл. 14.1 [2]. В однопролетной раме с жестким сопряжением ригеля с колонной верхний конец колонны закреплен только от поворота: 
.
Таким образом для нижней части колонны:
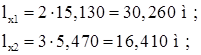
Находим расчетные длины из плоскости рамы:
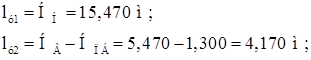
5.1 Проектирование верхней части колонны
Выбираем наиболее невыгодную комбинацию усилий: 
; N=-224 кН. Вычисляем требуемую площадь поперечного сечения верхней части колонны:
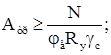
где 
– коэффициент надежности по назначению;
– коэффициент снижения расчетного сопротивления при внецентренном сжатии по табл. 74 СНиП.
Для определения вычисляем предварительные характеристики сечения:
Радиус инерции:
,
где hB =70 см. – высота сечения верхней части колонны.
Ядровое расстояние:
Условная гибкость:
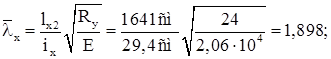
Относительный эксцентриситет:
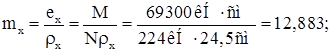
Задаемся отношением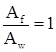 
.
Приведенный относительный эксцентриситет:
,
где: 
По табл. 74 СНиП 
.
Высота стенки будет равна 
(Принимаем толщину полок 1,6 см).
При 
наибольшая условная гибкость (табл. 27 СНиП):
Из условия местной устойчивости находим толщину стенки:
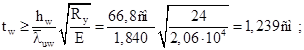
Принимаем толщину стенки tw
=0,8 см. Стенка получается заведомо неустойчивой, потому в расчетную площадь сечения колонны будем включать только пояса и примыкающие к ним участки стенки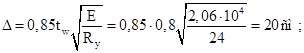 
Определяем требуемую площадь одного пояса:
Из условия устойчивости верхней части колонны из плоскости рамы:
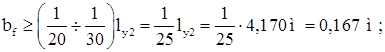
Принимаем 
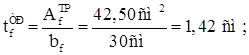
Проверяем пояс из условия обеспечения местной устойчивости:
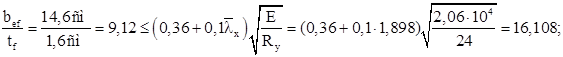
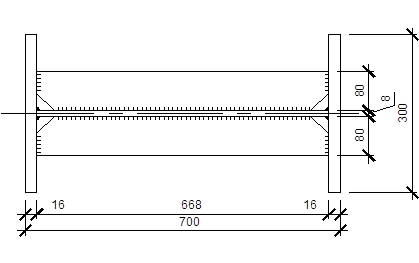
Рис. 34. Сечение верхней части колонны
Определяем фактические характеристики скомпонованного сечения:
Редуцированная площадь сечения:
Моменты инерции:
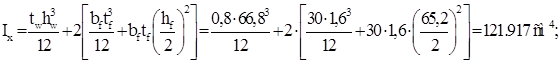
Радиусы инерции:
, 
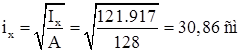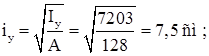
Момент сопротивления:
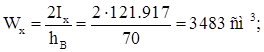
Ядровое расстояние:
Проверяем устойчивость верхней части колонны в плоскости рамы:
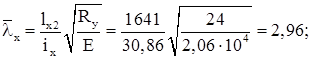
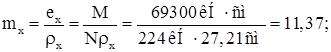
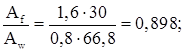
По приложению 8 СНиП: 
.
Приведенный относительный эксцентриситет:
По табл. 74 СНиП 
.
Устойчивость колонны в плоскости действия момента:
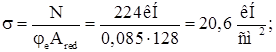
Оцениваем недонапряжение:
;
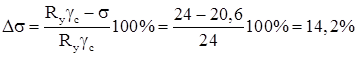Проверяем устойчивость верхней части колонны из плоскости рамы:
.
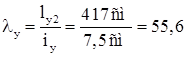
Найдем максимальный момент в пределах средней трети расчетной длины стержня:
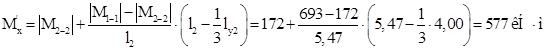
где:
– расчетный момент, по которому проектируется колонна;
– соответствующий момент в сечении 2–2 при тех же номерах нагрузок, что и М1-1
.
При изгибе колонн относительно оси y материал стенки работает в упругой стадии, поэтому устойчивость стенки проверяем по упругим формулам.
Наибольшее сжимающее напряжение в стенке:
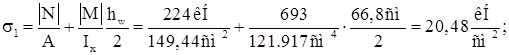
Соответствующее напряжение у противоположного края стенки:
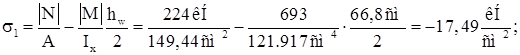
Среднее касательное напряжение в стенке:
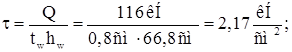
где:
– поперечная сила в сечении 1–1 при тех же номерах нагрузок, что М и N.
Определяем коэффициенты:
;
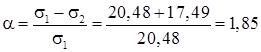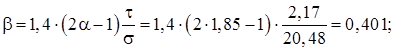
При 
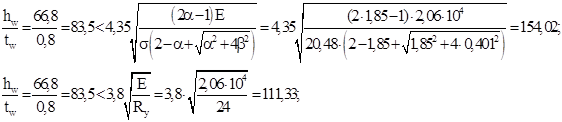
Условие не выполняется, стенка неустойчива. Включаем в расчет стенки два участка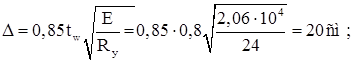 
Относительный эксцентриситет:
.
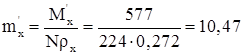Определяем коэффициент c, учитывающий влияние изгибающего момента на устойчивость из плоскости его действия, т. к. mx 10:
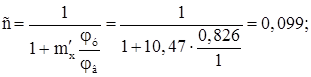
Устойчивость из плоскости рамы обеспечена.
Т.к.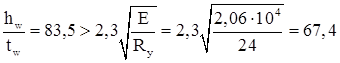 
, то следует укрепить стенку поперечными ребрами жесткости.
Ширина выступающей части парного симметричного ребра:
Принимаем:
Толщина ребра:
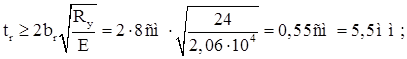
Принимаем:
5.2 Проектирование нижней части колонны
Сечение нижней части колонны сквозное, состоящее из двух ветвей, соединенных решеткой. Высота сечения 
. Подкрановую ветвь колонны принимаем из двутавра, наружную – составного сечения в виде швеллера.
Рис. 35. Сечение нижней части колонны
Из таблицы 2 выбираем наиболее невыгодные комбинации усилий для ветвей (сечения 3–3, 4–4).
Для подкрановой ветви (в. 1):
; 
.
Для наружной ветви (в. 2):
; 
.
Задаемся 
.
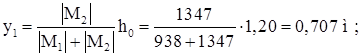
Усилие в подкрановой ветви:
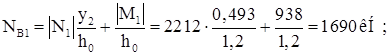
Усилие в наружной ветви:
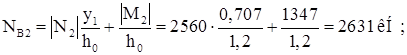
Определяем требуемую площадь ветвей, задаваясь коэффициентом продольного изгиба 
:
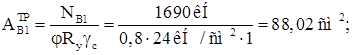
Для подкрановой ветви принимаем двутавр 50Б2:
; 
;
; 
;
; 
;
; 
;
.
Для наружной ветви:
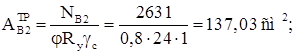
Компонуем сечение наружной ветви:
Принимаем 
.
Пусть 
Условная гибкость стенки (предварительно задаемся гибкостью 
):
.
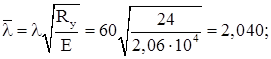
Назначаем толщину стенки швеллера 
, ширину пояса 
Требуемая толщина пояса:
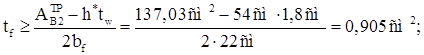
Принимаем 
Из условия местной устойчивости пояса швеллера:
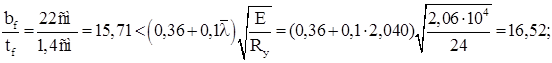
Проверяем местную устойчивость стенки швеллера:
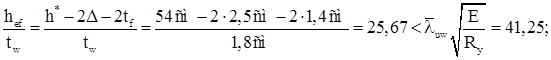
Устойчивость стенки обеспечена.
Определяем геометрические характеристики ветви:
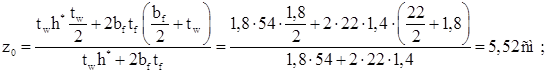
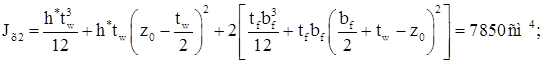
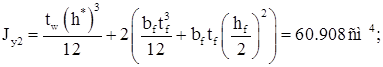
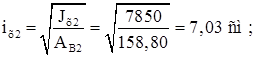
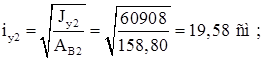
Уточняем положение центра тяжести колонны.
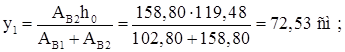
Отличие от первоначально принятых размеров менее 5%, поэтому усилия в ветвях не пересчитываем. Проверяем устойчивость каждой ветви как центрально сжатого стержня из плоскости рамы (относительно оси y).
Подкрановая ветвь:
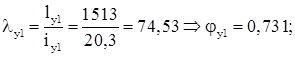
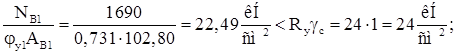
Устойчивость ветви обеспечена.
Наружная ветвь:
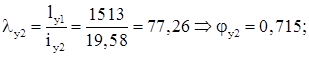
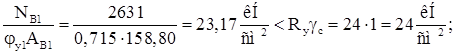
Устойчивость ветви обеспечена.
Из условия равноустойчивости каждой ветви в плоскости и из плоскости рамы находим максимальное возможное расстояние между узлами решетки:
Для подкрановой ветви:
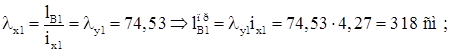
Для наружной ветви:
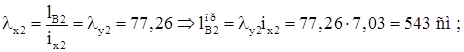
Принимаем высоту траверсы htr =63 см.
Проверяем устойчивость каждой ветви в плоскости рамы относительно осей 1–1 и 2–2 на участках между узлами решетки:
Подкрановая ветвь:
Наружная ветвь:
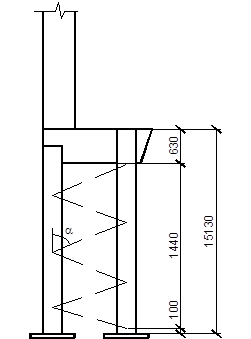
Рис. 36. Схема колонны
На участке Нреш =1440 мм должно уложиться равное количество панелей.
Принимаем угол наклона раскоса 
Расстояние между узлами решетки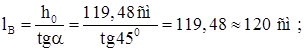 
Принимаем число панелей: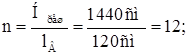 
Фактическая поперечная сила в сечении колонны Qmax =166 кН.
Условная поперечная сила:
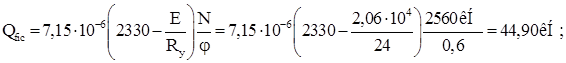
где N=2560 кН – наибольшее усилие в сквозной колонне;
– предварительное значение коэффициента продольного изгиба.
Т.к. 
расчет ведем по Qmax
.
Усилие сжатия в раскосе:
Задаемся гибкостью раскоса =90, находим соответствующий р =0,642 и определяем требуемую площадь раскоса:
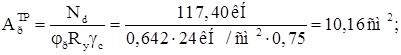
Здесь 
– коэффициент условий работы (учитываем, что раскос из уголка и крепится к ветви одной полкой).
Принимаем равнополочный уголок 808: Aр =12,29 см2 , imin =1,57 см.
Геометрическая длина раскоса 
Максимальная гибкость раскоса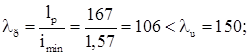 
По гибкости раскоса находим min =0,540 и проверяем устойчивость раскоса:
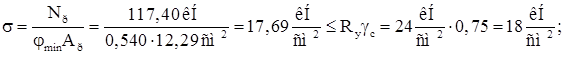
Проверяем устойчивость колонны как единого составного стержня в плоскости рамы. Определяем геометрические характеристики всего сечения:
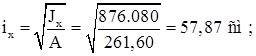
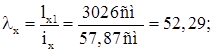
Приведенная гибкость:
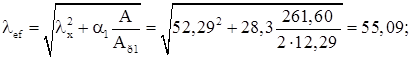
где 
=28,3 – коэффициент, зависящий от угла наклона раскосов.
Условная приведенная гибкость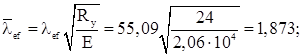 
Вычисляем относительные эксцентриситеты.
Для подкрановой ветви:
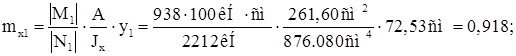
Для наружной ветви:
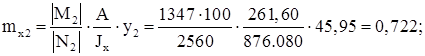
По приложению 9 [2] определяем коэффициенты 
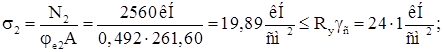
Устойчивость сквозной колонны в плоскости рамы обеспечена. Устойчивость сквозной колонны как единого стержня из плоскости действия момента проверять не нужно, так как она обеспечена проверкой устойчивости отдельных ветвей относительно оси у.
Для того, чтобы колонна сохраняла первоначальную форму и не закручивалась, в сквозных колоннах ставят поперечные диафрагмы через 3–4 м по высоте колонны (не менее 2-х на отправочную марку).
5.3 Расчет базы колонны
Раздельные базы под сквозные колонны устраивают при ширине колонны 1 м и более. Так как ветви сквозной колонны работают на осевые силы, то базы рассчитывают и конструируют как для центрально сжатой колонны. При этом центр опорной плиты совмещают с центром тяжести каждой ветви (иначе в ветви может появиться дополнительный изгибающий момент).
Максимальное усилие в нижнем сечении наружной ветви:
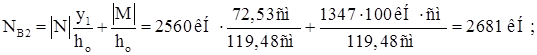
Требуемая площадь опорной плиты базы:
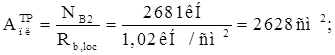
Здесь:
– расчетное сопротивление бетона класса В15 смятию.
Вылет плиты с2 =50 мм. Тогда габариты плиты:
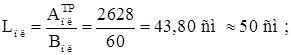
Давление под плитой считаем равномерно распределенным:
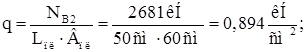
Из условия симметричного расположения траверс относительно центра тяжести ветви расстояние между траверсами в свету:
При толщине траверсы tтр =12 мм:
Определяем изгибающие моменты на отдельных участках плиты:
здесь =0,125 при b/a=45,8/22=2,08;
здесь =0,125 при b/a=45,8/12,76=3,59;
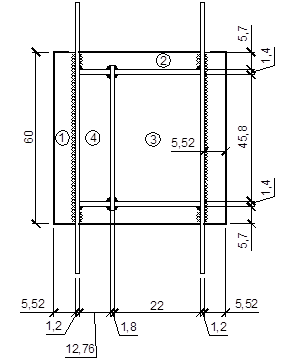
Рис. 37. К расчету базы колонны
По наибольшему из найденных изгибающих моментов определяют требуемую толщину плиты 
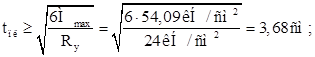
Принимаем опорную плиту из двух плит толщиной 2 см (22 см=4 см), Ry =24 кН/см2 .
Из предположения, что вся нагрузка со стержня колонны передается на ветви траверсы через вертикальные угловые швы, определяем высоту траверсы.
Сварку принимаем полуавтоматическую, положение швов нижнее.
Сварочные материалы: сварочная проволока Св-08ГА, электроды Э46.
, Rwf
=200 МПа;
, 
Принимаем hтр =36 см.
– Условие выполняется.
Проверяем прочность траверсы. Траверсы работают как двухконсольные балки под действием отпора бетона фундамента. Погонная нагрузка на одну ветвь траверсы равна:
Сила, действующая на одну ветвь траверсы:
В опорном сечении траверсы:
Рис. 38. Расчетная схема траверсы
Выбираем наибольшее значение поперечной силы Q1 =542,85 кН в опорном сечении. Момент в консоли:
Прочность траверсы по касательным напряжениям:
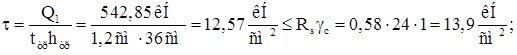
Прочность траверсы по нормальным напряжениям:
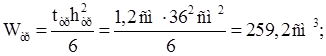
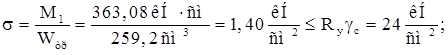
Прочность траверсы по редуцированным напряжениям:
В пролетном сечении траверсы Q2 =0.
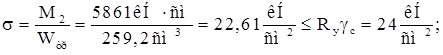
Рассчитывают горизонтальные угловые швы, которыми траверсы приварены к опорной плите. Суммарная длина горизонтальных швов:
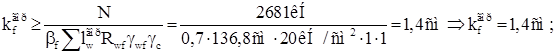
Рассчитаем анкерную плиту:
Комбинация усилий для расчета анкерных болтов: N=-702 кН; 
. Растягивающее усилие в анкерных болтах:
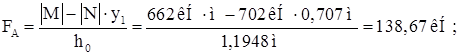
Требуемая площадь сечения одного болта:
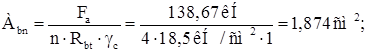
Конструктивно принимаем анкерные болты М24 с площадью сечения нетто Аbn =3,52 см2 . Диаметр отверстия в анкерной плите составляет 27 мм. Размеры сечения плиты 12030 мм.
6. Расчет стропильной фермы
6.1 Сбор нагрузок на ферму
Постоянная нагрузка на любой узел фермы равна:
где qкр =4,05 кН/м2 – расчетная поверхностная нагрузка от покрытия;
bф =12 м – шаг ферм;
d1 =d2 =3 м – длины примыкающих к узлу панелей.
Расчетная снеговая нагрузка в узел:
При жестком сопряжении фермы с колоннами на ферму передаются опорные изгибающие моменты. Определяем опорные изгибающие моменты по таблице расчетных усилий (табл. 2) в двух комбинациях.
Комбинация №1. Максимальный отрицательный момент в сечении 1–1: 
Соответствующий момент в верхнем сечении правой стойки: 
Комбинация №2.
Моменты, аналогичные моментам первой комбинации, но без учета снеговой нагрузки: 
Т.к. ферма входит в состав каркаса, то дополнительно учитываем передаваемый на нее распор рамы. Распор рамы определяем в двух комбинациях.
Комбинация №1.
Максимальный распор от действия всех нагрузок (по эпюрам продольных сил в ригелях):
- слева, 
- справа.
Комбинация №2.
Распор без учета снеговой нагрузки.
- слева,
- справа.
6.2 Статический расчет фермы
Распор рамы считаем приложенным к нижнему поясу фермы. Расчетной принимаем вторую комбинацию распора.
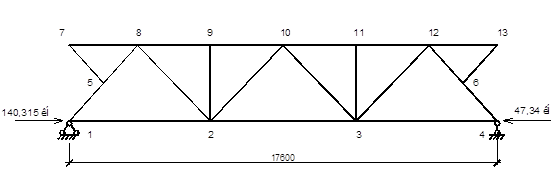
Рис. 39. Расчетная схема приложения распора
Усилия в стержнях нижнего пояса фермы от распора:
Для определения усилий от постоянной и снеговой нагрузок находим усилия в стержнях фермы от единичных сил, приложенных к верхнему поясу фермы (рис. 40).
Рис. 40. Расчетная схема для определения усилий от единичных сил
Для определения усилий от опорных моментов находим усилия в стержнях фермы от единичного момента, приложенного сначала к левой опоре (рис. 41), затем к правой (рис. 42).
Для удобства расчета единичный момент раскладываем на пару сил:
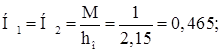
где hо – расстояние между осями поясов фермы на опоре.
где hоп =2,25 м – габарит фермы;
Длина фермы L=17,6 м. Углы наклона раскосов 
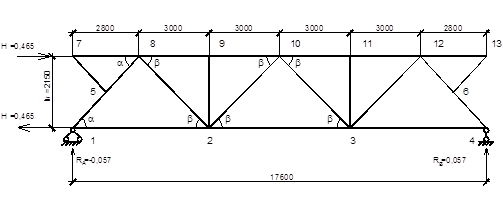
Рис. 41. Расчетная схема для определения усилий от единичного момента на левой опоре
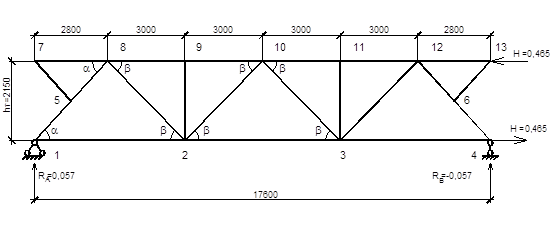
Рис. 42. Расчетная схема для определения усилий от единичного момента на правой опоре
Усилия от единичных сил и моментов находим методом вырезания узлов. Найденные усилия сводим в табл. 3, где также указываем усилия от постоянной и снеговой нагрузок, от опорных моментов, получаемых путем умножения усилий от единичных сил и моментов на значения сил.
6.3 Подбор сечений элементов фермы
Ферма принята с поясами из широкополочных тавров и решеткой из спаренных равнополочных уголков, которые соединяются через прокладки толщиной 10 мм. Сжатые элементы подбираются из требования общей устойчивости. В соответствии с требуемыми радиусами инерции и площадью сечения по сортаменту выбираем нужный номер профиля.
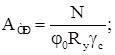
где 
определяется по гибкости 
(для поясов, опорного раскоса) и 
(для остальных элементов решетки).
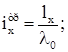
Принятое сечение проверяем на общую устойчивость. Растянутые элементы подбираются из условия прочности. В соответствии с требуемой площадью сечения по сортаменту выбираем необходимый номер профиля.
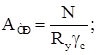
Принятое сечение проверяем на прочность. Результаты расчета сведены в таблицу 6.
6.4 Расчет сварных швов прикрепления решетки
Сварку узлов фермы принимаем полуавтоматическую порошковой проволокой ПП-АН8 (Rwf
=215 МПа) в нижнем положении (
). Тип электрода Э50. Определяем расчетное сечение:
расчетное сечение проходит по металлу шва.
Длины сварных швов, которыми раскосы и стойки из равнополочных уголков прикрепляются к фасонкам и поясам фермы, определяются по следующим формулам:
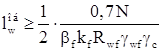– по обушку;
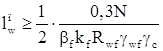– по перу;
Катеты швов kf принимаются в соответствии с минимально допустимыми катетами швов и с учетом условий:
– для швов по перу уголка; 
– для швов по обушку уголка.
Расчет швов приведен в таблице 7.
Табл. 7. Катеты сварных швов
| № стержня | Сечение , мм | N, кН | Шов по обушку | Шов по перу | ||||
| Nоб =0,7N, кН | kf , см | lw , см | Nоб =0,3N, кН | kf , см | lw , см | |||
| 1–8 | 16010 | 661 | 467 | 0,8 | 20 | 200 | 0,8 | 9 |
| 2–8 | 807 | 432 | 305 | 0,6 | 17 | 131 | 0,6 | 8 |
| 2–10 | 807 | 173 | 122 | 0,6 | 7 | 53 | 0,6 | 5 |
| 2–9 | 705 | 152 | 106 | 0,5 | 7 | 47 | 0,5 | 5 |
Список литературы
1. СНиП II-23–81*. Стальные конструкции. Нормы проектирования. М.: ЦИТП Госстроя СССР. 1990.
2. Металлические конструкции. Общий курс: Учебник для вузов / Под общ. ред. Е.И. Беленя. М.: Стройиздат, 1986.
3. Расчет стальных конструкций: Справочное пособие Я.М. Лихтарников и др. – 1984.