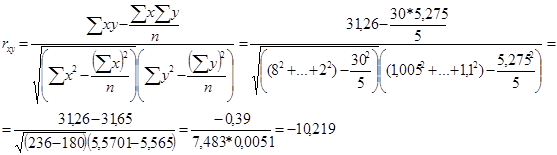Статистические расчеты 2
СОДЕРЖАНИЕ: Задача 1. На основании данных выборочного наблюдения была произведена группировка количества разговоров по длительности: Длительность разговора, мин.Задача 1. На основании данных выборочного наблюдения была произведена группировка количества разговоров по длительности:
Длительность разговора, мин. |
3–5 | 5–7 | 7–9 | 9–11 | 11–13 | Свыше 13 | Всего разговоров |
| Число разговоров | 90 | 85 | 70 | 60 | 30 | 5 | 340 |
Выполнить вторичную группировку, чтобы обеспечить представительность последней группы. Образовать 4 группы с неравными интервалами: 3–5, 5–8, 8–12, свыше 12 мин.
Решение:
Проведём вторичную группировку:
Длительность разговора, мин. |
3–5 | 5–8 | 8–12 | Свыше 12 | Всего разговоров |
| Число разговоров | 90 | 108 | 117 | 25 | 340 |
Задача 2. По следующим данным сравнить состав занятого населения двух областей, вычислив относительный показатель, характеризующий соотношение между численностью работников производственной деятельности и работников двух других сфер деятельности
| Категории деятельности | Количество работников, чел. | |
| В I области | Во II области | |
| Сфера производства | 3250 | 2560 |
| Аппарат управления | 320 | 390 |
| Прочие виды деятельности | 670 | 740 |
Решение:
Определим относительную величину между численностью работников производственной сферы деятельности и других сфер деятельности по областям:
- между численностью сферы производства и аппарата управления:
а) для области I:
![]()
б) для области II:
![]()
Вывод: на численность производственной сферы работников аппарата управления во второй области приходиться на 5,38% больше, чем в первой (15,23 – 9,85)
- между численностью сферы производства и прочими видами деятельности:
а) для области I:
![]()
б) для области II:
![]()
Вывод: на численность производственной сферы работников других видов деятельности во второй области приходиться на 8,29% больше, чем в первой (28,91 – 20,62)
Задача 3. Определите среднюю производительность труда в целом по предприятию в I полугодии по следующим данным:
| Цех | Производительность труда, млн. р./чел. | Среднесписочное число работников, чел. |
| № 1 | 80 | 60 |
| № 2 | 68 | 50 |
| № 3 | 55 | 30 |
Определите, как колеблется данный показатель.
Решение:
Рассчитаем среднюю производительность труда по формуле средней арифметической взвешенной:
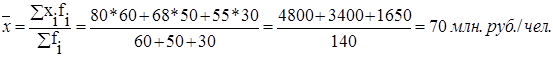 ,
,
где ![]() – средняя производительность труда по предприятию;
– средняя производительность труда по предприятию; ![]() – производительность труда рабочего в i-м цехе;
– производительность труда рабочего в i-м цехе; ![]() – число рабочих;
– число рабочих; ![]() – производительность труда рабочих i-го цеха завода.
– производительность труда рабочих i-го цеха завода.
Рассчитаем размер вариации:
1) дисперсия (2 )
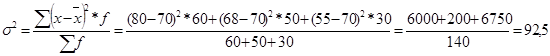
2) среднее квадратичное отклонение ():
![]()
3) коэффициент вариации (V):
![]() .
.
Задача 4. По данным задачи 1:
1) определите среднее значение изучаемого признака, моду и медиану;
2) постройте гистограмму;
3) оцените характер асимметрии.
Решение:
Рассчитаем среднее значение изучаемого признака:
![]()
Рассчитаем моду:
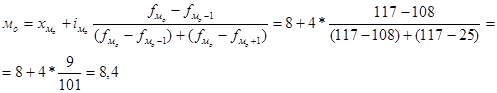
где ![]() – начало (нижняя граница) модального интервала;
– начало (нижняя граница) модального интервала; ![]() – величина интервала;
– величина интервала; ![]() – частота модального интервала;
– частота модального интервала; ![]() – частота интервала, предшествующего модальному;
– частота интервала, предшествующего модальному; ![]() – частота интервала, следующего за модальным.
– частота интервала, следующего за модальным.
Рассчитаем медиану:
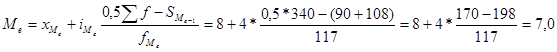
где ![]() – начало (нижняя граница) медианного интервала;
– начало (нижняя граница) медианного интервала; ![]() – величина интервала;
– величина интервала; ![]() – сумма всех частот ряда;
– сумма всех частот ряда; ![]() – сумма накопленных частот вариантов до медианного;
– сумма накопленных частот вариантов до медианного; ![]() – частота медианного интервала.
– частота медианного интервала.
Построим график интервального ряда распределения:(гистограмма):
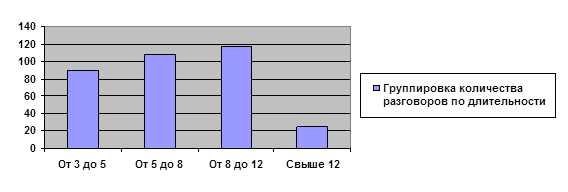
Так как М0
МЕ
![]() , то перед нами левосторонняя асимметрия.
, то перед нами левосторонняя асимметрия.
Задача 5. Ежегодные темпы прироста продукции (в % к предыдущему году) составили:
| Годы | 1-й | 2-й | 3-й | 4-й | 5-й |
| Темпы прироста | 2,4 | 1,7 | 2,0 | 1,5 | 2,8 |
Вычислите за приведенные годы базисные темпы роста по отношению к начальному (базисному) году и среднегодовые темпы роста и прироста за весь период.
Решение:
Рассчитаем средний уровень ряда по формуле средней арифметической простой:
![]() ,
,
В зависимости от задачи исследования абсолютные приросты (снижения) y, темпы прироста (снижения) Т
Рассчитаем базисные темпы роста по отношению к начальному году:
- 2-ой год по отношению к 1-му:
![]()
- 3-ий год по отношению к 1-му:
![]()
- 4-ый год по отношению к 1-му:
![]()
- 5-ый год по отношению к 1-му:
![]()
Рассчитаем среднегодовой темп роста за весь период:
![]()
Рассчитаем среднегодовой темп прироста:
![]()
Задача 6. По следующим данным исчислите общий и индивидуальные индексы себестоимости и сумму экономики.
| Изделие | Затраты на товарную продукцию, млрд. р. | Объем производства в отчетном году, тыс. ед. | Снижение себестоимости единицы продукции по сравнению с базисным периодом, % |
| А | 220 | 4,5 | 7,5 |
| Б | 305 | 6,0 | 4,5 |
| В | 148 | 2,8 | 3,0 |
Решение:
Рассчитаем затраты на товарную продукцию в базисном периоде:
- для изделия А:
Z0 = 220 + 220 * 7,5 % = 236,5 млн. руб.
- для изделия Б:
Z0 = 305 + 305 * 4,5 % = 318,725 млн. руб.
- для изделия В:
Z0 = 148 + 148 * 3,0 % = 152,44 млн. руб.
Рассчитаем общий индекс:
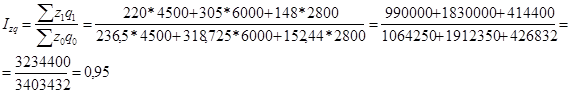
Рассчитаем индивидуальные индексы:
- для изделия А:
![]()
- для изделия Б:
![]()
- для изделия В:
![]()
Рассчитаем экономию по каждому изделию:
- по изделии А:
Э = Z1 – Z0 = 220 – 236,5 = - 16,6 млн. руб.
- по изделии Б:
Э = Z1 – Z0 = 305– 318,725 = - 13,725 млн. руб.
- по изделию В:
Э = Z1 – Z0 = 148 – 152,44 = - 4,44 млн. руб.
Задача 7. В отчетном периоде произошло снижение цен на 5% при увеличении физического объема продукции на 15%. Определите:
1) изменение стоимости продукции в отчетном периоде по сравнению с базисным периодом;
2) абсолютное изменение стоимости продукции за счет изменения физического объема продукции;
3) абсолютное и относительное изменение стоимости продукции за счет изменения цен.
Решение:
Рассчитаем стоимость продукции и физический объём:
q1 = q0 + q0 * 15 % = q0 + 0,15 * q0 = 1,15 * q0
P1 = P0 – P0 *5 % = Р0 – 0,05 * Р0 = 0,95 * Р0
Таким образом, изменение стоимости в отчетном периоде по сравнению с базисным:
![]()
Рассчитаем абсолютное изменение стоимости продукции за счёт изменения физического объёма продукции:
![]()
Рассчитаем абсолютное и относительное изменение стоимости продукции за счет изменения цен:
![]()
Задача 8. Изменение средней годовой численности работников отрасли характеризуется следующими данными:
| Годы | 1980 | 1990 | 2000 | 2005 (прогноз) |
| Численность работников, тыс. чел. | 153,2 | 226,1 | 315,9 | 340,5 |
Изобразите эти данные в виде графиков: а) прямоугольных (столбиковых и ленточных); б) квадратных. Какой из этих графиков наиболее наглядно изображает изменение численности работников в данной отрасли за 1980-2005 гг.? Сформулируйте выводы, следующие из графических изображений.
А) - Столбиковая:
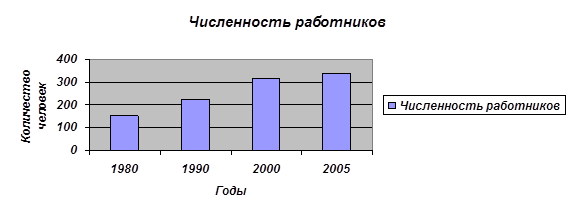
- Ленточная:
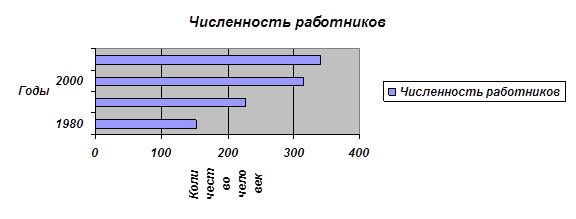
б) Квадратная:
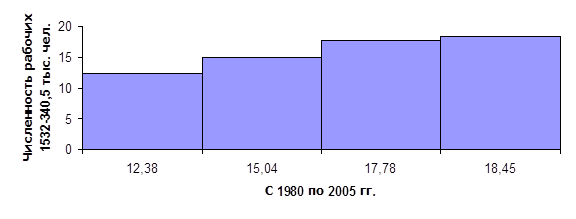
На мой взгляд, наиболее полно отражает изменение численности работников в данной области столбиковая диаграмма. В соответствии с данными графиков, можно сделать вывод, что на протяжении 1980 – 2005 гг. численность работников увеличилась в два раза и продолжает расти.
Задача 9. Хронометраж работы станочника дал следующие результаты:
| Затраты времени на изготовление одной детали, мин. | 20–21 | 21–22 | 22–23 | 23–24 |
| Число изготовленных деталей | 6 | 13 | 10 | 7 |
Определите среднюю трудоемкость изготовления детали и предельную ошибку этого показателя с вероятностью 0,954, учитывая, что хронометраж производится при массовом выпуске. Какие результаты получатся, если взять вероятность 0,997?
Решение:
Рассчитаем среднюю трудоёмкость изготовления детали:
![]()
Рассчитаем среднюю внутригрупповую дисперсию:
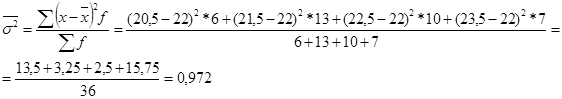
Рассчитаем среднюю ошибку выборочной средней при повторном отборе
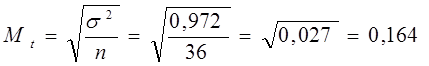
где ![]() – дисперсия выборочной совокупности; n – объем (число единиц) выборки.
– дисперсия выборочной совокупности; n – объем (число единиц) выборки.
Рассчитаем предельную ошибку выборки, при , t = 2 (для p=0,954):
![]()
Рассчитаем предельную ошибку выборки, при , t = 3 (для p=0,997):
![]()
Задача 10. Имеются следующие данные о продолжительности производственного стажа и среднем проценте выполнения норм выработки по 30 рабочим-сдельщикам цеха о продолжительности производственного стажа и среднем проценте выполнения норм выработки:
| Группы рабочих по продолжительности стажа работы, лет | Число рабочих, чел. | Средний процент выполнения норм выработки одним рабочим |
| До 5 | 8 | 100,5 |
| 5–10 | 10 | 104,0 |
| 10–15 | 8 | 106,0 |
| 15–20 | 2 | 107,0 |
| 20 и более | 2 | 110,0 |
Определите:
1)средний процент выполнения норм выработки по цеху;
2) вид корреляционной зависимости между данными показателями;
3) параметры уравнения регрессии;
4) тесноту изучаемой связи.
Решение:
Рассчитаем средний процент выполнения норм выработки по цеху:
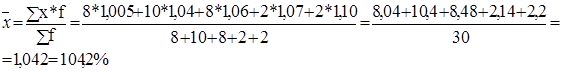
Определим вид корреляционной зависимости между данными показателями:
В качестве линии регрессии используем уравнение прямой:
![]() ,
,
где y – результативный (зависимый) признак; x – факторный (независимый) признак; a и b – параметры уравнения прямой.
Для определения параметров a и b по методу наименьших квадратов составляется система двух нормальных уравнений:
![]()
![]()
![]() ,
,
![]() .
.
Решая эту систему уравнений, находим:
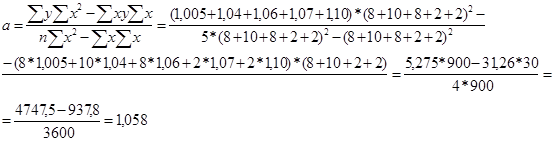
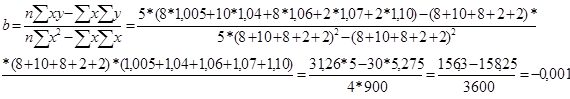
Для измерения тесноты данной связи используем коэффициент корреляции, исчисляемый по формуле: