Стоимость и доходность отдельных видов ценных бумаг
СОДЕРЖАНИЕ: Стоимостная оценка акции. Методы оценки акций. Определение курсовой стоимости акции. Стоимостная оценка облигации. Ценообразование бескупонной облигации. Облигации с постоянным купонным доходом. Понятие доходность к погашению (доходность до погашения).1. Стоимостная оценка акции
При принятии инвестиционных решений в процессе анализа рынка ценных бумаг используются различные стоимостные оценки акций. В практической деятельности различают следующие их виды:
1) номинальная стоимость;
2) эмиссионная стоимость (цена размещения);
3) бухгалтерская (балансовая, книжная) стоимость;
4) рыночная стоимость;
5) курсовая стоимость.
Номинальная стоимость акции - это стоимость, указанная на лицевой стороне акции или ее сертификата. Оплата акций при учреждении общества производится учредителями по их номинальной стоимости. В начальный период функционирования общества стоимость его имущества равна величине уставного капитала.
В процессе своей деятельности стоимость имущества предприятия может увеличиваться или уменьшаться. Таким образом, с течением времени реальная стоимость имущества акционерного общества (АО) будет отличаться от величины уставного капитала. В этой связи возникает необходимость в определении бухгалтерской стоимости акции, которая представляет собой отношение стоимости чистых активов компании к количеству размещенных акций. Балансовая стоимость обычно рассчитывается ежеквартально и в конце года при составлении баланса.
Под стоимостью чистых активов АО понимается величина, исчисляемая вычитанием из суммы активов АО, принимаемых к расчету, суммы его пассивов, принимаемых к расчету. В состав активов, принимаемых к расчету, относят: внеоборотные и оборотные активы, за исключением сумм, затраченных на выкуп собственных акций и задолженности учредителей по взносам в уставный капитал. В состав пассивов, включаемых в расчет, включают: долгосрочные и краткосрочные обязательства АО.
В процессе своего развития АО периодически прибегает к эмиссии акций с целью получения дополнительного капитала. Цена, по которой реализуются акции нового выпуска, называется ценой размещения (эмиссионной ценой). По российскому законодательству размещение акций должно осуществляться по рыночной цене, которая может отличаться от номинальной. Если в процессе обращения на вторичном рынке сделки по купле-продаже акций могут совершаться по цене выше или ниже их номинальной стоимости, то при эмиссии акций цена их размещения должна быть не ниже номинальной.
Рыночная цена - это цена, по которой акция покупается и продается на вторичном рынке. Эта цена формируется под влиянием рыночной конъюнктуры и определяется спросом и предложением, уровнем доходности на смежных сегментах финансового рынка, инфляционными ожиданиями и другими факторами. Рыночная цена обычно устанавливается на торгах на фондовой бирже и отражает действительную цену акции при условии большого объема сделок.
В отличие от других ценных бумаг оценка обыкновенных акций несет в себе определенные трудности для инвестора. Это связано с тем, что:
1) существуют трудности в оценке первой составляющей дохода владельца акции - дивидендов. Размер дивидендов по обыкновенным акциям не известен, и поэтому текущая оценка будущих дивидендов строится на предположениях инвестора;
2) неопределенность в движении курса акции. В отличие от долговых ценных бумаг, у которых рыночная цена связана с номиналом и постоянно приводится в соответствии с требуемой доходностью и риском к ней, цена акции не носит такой зависимости. Рыночная цена акции в большей степени определяется ростом чистых активов компании, и ее максимальное значение не ограничено. При этом она может как расти, так и снижаться, при том что направление ее движения строится также на прогнозах инвесторов;
3) бессрочный характер акции требует учета планов инвестора по отношению к ней. Это связано с подходом к оценке ценных бумаг с определенным и неопределенным сроком владения, так как оценка происходит на основе дисконтирования будущих потоков платежей.
Определение цены акции, как и большинства ценных бумаг, базируется на текущей оценке денежных потоков, которые инвестор получит в будущем. Так при определении цены акции инвестор учитывает размер будущих дивидендов и ожидаемую стоимость акции в конце инвестиционного периода. Причем прогноз и будущих дивидендов, и изменение цены акции строятся на основании политики акционерного общества в отношении этих показателей и анализе динамики изменений их за предыдущий период. Поэтому оценки будущих доходов от акций носят условный характер. Исключение составляют привилегированные акции, размер дивидендов по которым определен в уставе.
Отметим, что доход в форме дивидендов может быть представлен в виде серии равных платежей и платежей произвольной формы. В связи с этим различаются методы оценки акций. Если инвестор, приобретая акцию на неопределенный период, рассчитывает только на доход в форме дивидендов, то курсовая цена акции для него будет определяться как
![]()
где PV – текущая стоимость акции;
t – период, в котором были выплачены дивиденды;
Divt – дивиденд, который будет выплачен в периоде t;
r- ставка дисконтирования (доходность), которая соответствует уровню риска инвестирования в акции данного акционерного общества.
При этом если дивиденды выплачиваются равными платежами, то используют следующую формулу:
![]()
Как видно из формулы (4.1), она неудобна для определения курсовой стоимости акции, поскольку сложно определить уровень дивидендов которые уходят в бесконечность, так как акция является бессрочной бумагой. Формула (4.1) несколько видоизменится, если инвестор, владеющий акцией, планирует держать ее в течение определенного периода времени, получая дивиденды, и затем продать ее:
![]()
где FV – цена акции в конце периода n, когда инвестор планирует ее продать.
В формуле (4.3) как и в формуле (4.1) сложность возникает как с прогнозированием дивидендов, так и с прогнозированием цены будущей продажи акции. Простейшая модель прогнозирования дивидендов предполагает, что они будут расти с постоянным темпом. Тогда дивиденд для любого года можно рассчитать по формуле:
Divt =Div0 (1+g)t (4)
где Div0 – дивиденд за текущий год;
g – темп прироста дивидендов.
Более удобно определять курсовую стоимость по следующей формуле:
![]()
где Div1 – дивиденд будущего года, который можно определить по формуле (4).
Формула (4.5) выведена для следующих условий: предполагается, что дивиденд растет с постоянным темпом и r g.
Пример.
За прошедший год дивиденд составил 100 руб. на акцию, темп прироста дивиденда равен 5%, ставка дисконтирования составляет 25%. Определить курсовую стоимость акции.
Решение.
Div1 =100(1+0,05)=105 руб.
![]()
Рыночная цена в расчете на 100 денежных единиц (д.е.) номинала называется курсом:
![]() (6)
(6)
где Ka – курс акции;
Р – рыночная цена;
N – номинальная цена.
Пример.
Рыночная цена акции составляет 210 руб. Номинальная цена акции – 200 руб. Рассчитайте курс акции.
Решение.
![]()
Биржевой курс как результат биржевой котировки определяется равновесным соотношением спроса и предложения. Котировка предполагает наличие двух цен:
1) цены приобретения, по которой покупатель выражает желание приобрести акцию, или цены спроса, чаще называемой цена бид;
2) цены предложения, по которой владелец акции желает ее продать, или цена предложения, называемая оферта.
2. Доходность акции
Инвестиции в акции - разновидность финансовых инвестиций, то есть вложение денег в финансовые активы с целью получения дохода. Приобретая акции, инвестор предполагает получить доход от своих инвестиций выше среднерыночного. Доход от вложений в акции складывается из:
1) дивидендов;
2) изменения курсовой стоимости.
Рыночная текущая доходность, которая будет зависеть от уровня цены, существующей на рынке в каждый момент времени рассчитывается по следующей формуле:
![]()
![]() (7)
(7)
где Р – рыночная цена акции;
Div – сумма дивиденда за год.
Пример.
Рассчитайте текущую доходность акции, если известно, что ее рыночная цена составляет 500 руб., а выплаченный дивиденд – 50 руб.
Решение.
![]()
Синонимом термина «текущая доходность» является термин «ставка дивиденда». Ставка дивиденда показывает, какой уровень доходности инвестор получит на свои инвестиции за счет возможных дивидендов, если купит акцию по текущей цене.
После реализации ее держатель может получить, при благоприятном изменении цены акции, вторую составляющую совокупного дохода - прирост курсовой стоимости. Количественно это обозначается как доход, равный разнице между ценой реализации и ценой приобретения. При этом при превышении цены продажи над ценой покупки инвестор получает доход, а при снижении цен на фондовом рынке и соответственно цены реализации по сравнению с ценой приобретения инвестор понесет убытки.
Если инвестиционный период не включает выплаты дивидендов, то доход образуется как разница между ценой покупки и ценой продажи. При этом доходность рассчитывается как отношение разницы в цене продажи и цене покупки к затратам инвестора. Такая доходность называется конечной, так как он реализовал свою ценную бумагу и, следовательно, доход по ней ни в какой форме уже не получит:
![]() (8)
(8)
где Yf – конечная доходность;
S - цена продажи акции.
Если инвестиционный период, по которому оцениваются акции, включает выплату дивидендов и заканчивается их реализацией, то доход определяется как сумма совокупных дивидендов и изменения курсовой стоимости. Доходность обычно называется совокупной и рассчитывается по формуле:
![]() (9)
(9)
где n – количество лет владения акцией
или
![]() (10)
(10)
где T – количество дней владения ценной бумагой.
Пример.
Инвестор купил акцию за 4000 руб. и продал через три года за 5000 руб. За первый год ему выплатили дивиденд в размере 300 руб., за второй – 350 руб., за третий – 450 руб. Определить доходность акции.
Решение.
![]() годовых
годовых
3. Стоимостная оценка облигации
Облигации имеют нарицательную цену (номинальную) и рыночную цену. Номинальная стоимость облигации напечатана на лицевой стороне самой ценной бумаги и обозначает сумму, которая берется взаймы и подлежит возврату по истечении срока обращения. Как правило, облигации выпускаются с высокой номинальной стоимостью и рассчитаны на богатых инвесторов. Этим они также отличаются от акций, стоимость которых рассчитана на приобретение широким кругом лиц, при этом если для акций номинальная стоимость - величина довольно условная (так как акции продаются и покупаются по цене, никак не связанной с номиналом), то для облигаций номинальная стоимость является очень важным параметром. Это связано с тем, что по изначально зафиксированной величине номинала облигации будут погашаться по окончании срока их обращения.
С момента эмиссии и до погашения облигации продаются и покупаются по установившимся на рынке ценам. Рыночная цена в момент эмиссии может быть ниже номинала, равным ему или быть выше. С момента эмиссии рыночная цена облигаций определяется исходя из ситуации, сложившейся на рынке, а также двух главных элементов:
1) перспективы получить при погашении номинальную стоимость (чем ближе срок погашения, тем выше рыночная цена облигации);
2) права на регулярный фиксированный доход (чем выше процентный доход, тем выше рыночная цена).
Определение рыночной цены облигации зависит прежде всего от формы дохода, который она приносит своему владельцу. В этой связи различают:
1) облигации с нулевым купоном, или дисконтные, по которым инвестор доход получает в форме дисконта. Ценообразование бескупонной облигации заключается в определении величины элементарного потока платежей, по известным значениям номинальной стоимости, безрисковой процентной ставки (или ожидаемой доходности) и периода инвестирования. Таким образом, текущая цена облигации:
![]() (11)
(11)
где N - номинальная стоимость облигации.
При этом рыночная цена данной облигации никогда не превысит номинальную, так как при погашении инвестор получит только номинальную стоимость облигации.
Пример.
Номинальная стоимость бескупонной облигации равняется 1000 руб. На рынке доходность на инвестиции с уровнем риска, соответствующим данной облигации, оценивается в 20%. Срок обращения облигации – 3 года. Рассчитать текущую (курсовую) стоимость.
Решение.
![]() руб
руб
2) облигации с постоянным купонным доходом. Купонная ставка по таким облигациям зафиксирована и является неизменной на всем протяжении срока ее обращения. Рыночная цена такой облигации определяется как
![]() (12)
(12)
где С – купон;
N – номинал;
n – число лет до погашения облигации;
r – доходность к погашению.
Рыночная цена данных облигаций может быть как выше, так и ниже номинальной в зависимости от ожидаемой инвестором доходности и от ставки купона. В формуле (12) появилось такое понятие как доходность к погашению (доходность до погашения) – это доходность в расчете на год, которую обеспечит себе инвестор, если купив облигацию, продержит ее до погашения.
Пример.
Номинальная стоимость облигации равняется 10000 руб., купон 20%, доходность до погашения – 15%, до погашения остается три года. Рассчитайте рыночную цену облигации.
Решение.
![]() руб
руб
В данном случае цена облигации оказалась выше номинала. Такая ситуация объясняется тем, что, согласно условиям примера, рынок требует по облигации доходность до погашения на уровне 15% годовых. Однако по ней выплачивается более высокий купон – 20%. Каким образом инвестор может получит более низкую доходность, чем 20%? Это возможно лишь в том случае, если он приобретет облигацию по цене выше номинала. При погашении облигации ему выплатят только номинал. Поэтому сумма премии, которую он уплатил сверх номинала, уменьшит доходность его операции до 15%.
Поскольку номиналы у разных облигаций различаются, то для сопоставления рыночных цен облигаций используют курс. Курсом облигации называется значение рыночной цены облигации, выраженное в процентах к ее номиналу:
![]() (13)
(13)
где К – курс облигации;
Р – рыночная цена облигации;
N – номинальная цена облигации.
Пример.
Рассчитайте курс облигации, если известно, что рыночная цена облигации составляет 500 руб., а номинальная цена – 600 руб.
Решение.
![]()
4. Доходность облигации
Общий доход от облигации складывается из следующих элементов:
1) периодически выплачиваемых процентов;
2) изменения стоимости облигации за соответствующий период;
3) дохода от реинвестиций полученных процентов.
Облигация приносит своему владельцу фиксированный доход в виде процентов. Обычно проценты выплачиваются 1-2 раза в год. При этом, чем чаще производятся процентные выплаты, тем больший доход приносит облигация, ведь проценты могут быть реинвестированы. Размер купонного дохода по облигациям зависит прежде всего от надежности облигации, то есть от того, кто является эмитентом. Чем устойчивее компания и надежнее облигация, тем ниже предлагаемый процент. Кроме того, существует зависимость между процентным доходом и сроком обращения (чем больше срок обращения, тем выше должен быть процент), при этом чем больше срок обращения облигации, тем существеннее доход от реинвестиций.
Однако более существенной составляющей дохода от владения облигацией является доход от изменения стоимости облигации. При этом для владельцев облигаций с нулевым купоном – это единственный источник дохода. Доход по ним образуется как разница между номинальной ценой и рыночной ценой.
В зависимости от получаемого инвестором дохода различают:
1) текущую доходность облигации;
2) доходность до погашения облигации.
Показатель текущей доходности характеризует годовые (текущие) поступления по облигации относительно ее рыночной стоимости. Текущая доходность облигации рассчитывается по формуле:
![]() (14)
(14)
где Yc - текущая доходность облигации, %;
С – сумма выплаченных в год процентов, руб.;
PV – текущая цена облигации, руб.
Текущая доходность облигации является простейшей характеристикой облигации. В знаменателе формулы (14) стоит текущая цена облигации. В любой момент она может измениться, тогда измениться и значение текущей доходности. Показателем текущей доходности удобно пользоваться, когда до погашения облигации остается немного времени, так как в этом случае ее цена вряд ли будет сильно меняться.
Более объективным показателем является доходность до погашения, так как при ее определении учитывается не только купон и цена бумаги, но и период времени, который остается до погашения, а также скидка или премия относительно номинала. Формула ориентировочной доходности облигации имеет следующий вид:
![]() (4.15)
(4.15)
где Y – доходность до погашения;
N – номинал облигации;
PV – цена облигации;
n – число лет до погашения;
С – купон.
Пример.
Номинал облигации равен 1000 руб., текущая цена облигации 900 руб., число лет до погашения – 2 года, купон равен 5%. Определить доходность до погашения облигации.
Решение.
![]()
Погрешность формулы (15) тем больше, чем больше цена облигации отличается от номинала и чем больше лет остается до погашения облигации.
Доходность до погашения с нулевым купоном определяется по следующей формуле:
![]() (16)
(16)
Пример.
Номинал бескупонной облигации равен 1000 руб., текущая рыночная стоимость равна 900 руб., до погашения осталось два года. Определить доходность к погашению.
Решение.
![]()
5. Стоимостная оценка векселя
Доход по векселям может быть получен как в виде процентов, так и виде дисконта. В связи с этим различают два подхода к стоимостной оценке векселей.
Если вексель приносит своему владельцу доход только в виде дисконта, то сумма, которую инвестор получит при погашении, будет равна вексельной сумме или номинальной стоимости векселя.
При этом на рынке такой вексель будет обращаться по цене ниже номинальной, то есть с дисконтом:
PV=N–D. (17)
Величину дисконта определяют по следующей формуле:
![]() (18)
(18)
где t – количество дней до погашения векселя;
d – ставка дисконтирования, %;
N – номинал векселя.
Пример.
Номинал векселя равен 10000 руб., ставка дисконта равна 10%, до погашения векселя осталось 35 дней. Определить величину дисконта.
Решение.
![]() руб
руб
Отсюда рыночная стоимость дисконтного векселя:
![]() (19)
(19)
Пример.
Номинальная цена векселя 100000 руб., ставка дисконта 5%, до погашения остается 60 дней. Определить цену векселя.
Решение.
![]() руб.
руб.
Процентный вексель может приносить доход своему владельцу и в виде процентов, и в виде дисконта.
Сумма, которую инвестор получит при погашении процентного векселя, равна номиналу векселя и сумме начисленных процентов:
S=N +I (20)
При этом величина процентов определяется по следующей формуле:
![]()
где Tобр – период обращения векселя, дней;
R – вексельная процентная ставка, %.
Отсюда сумма, причитающаяся векселедержателю при погашении:
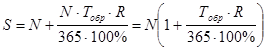 (22)
(22)
Пример.
Номинал векселя равен 20000 руб., по векселю начисляются 10% годовых, с начала начисления процентов до момента предъявления векселя к оплате прошло 60 дней. Определить сумму, которую получит держатель процентного векселя при его погашении.
Решение.
![]() руб.
руб.
На рынке такие векселя могут продаваться по цене как выше номинальной стоимости, так и ниже, в зависимости от доходности и риска. Процесс определения рыночной цены таких векселей можно представить как дисконтирование суммы, получаемой при погашении.
При этом сумма дисконта по процентному векселю определяется по следующей формуле:
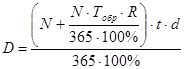 (23)
(23)
Отсюда рыночная цена процентного векселя определяется как
PV=N + I –D(24)
Или
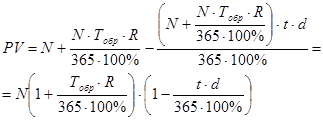 (25)
(25)
Пример.
Номинальная цена векселя составляет 300000 руб., по векселю начисляются 10% годовых, с начала начисления процентов до момента предъявления векселя к оплате прошло 90 дней, а число дней, оставшихся до погашения векселя составляет 10 дней. Ставка дисконта по векселю 5%. Определить текущую цену векселя.
Решение.
![]() руб.
руб.
6. Доходность векселя
При определении доходности по векселю, так же как и по облигациям, инвестор учитывает доход, полученный в форме процентов и дисконта.
Дисконтный вексель доход своему владельцу приносит только в виде дисконта. При этом доходность будет равна:
![]() (26)
(26)
где Р – цена приобретения векселя.
Пример.
Рассчитайте доходность дисконтного векселя, если известно, что цена приобретения векселя составляет 98000 руб., до погашения векселя осталось 30 дней, величина дисконта - 2000 руб.
Решение.
![]()
По процентному векселю доход обычно составляет сумма процентов или разницу между ценой погашения и номинальной стоимостью векселя. Однако, в связи с тем, что векселя обращаются по рыночным ценам, лучше доходом по векселю считать разницу между ценой погашения и ценой приобретения векселя.
Тогда доходность по процентному векселю рассчитывается по следующей формуле:
![]() (27)
(27)
где Pпог – цена погашения векселя.
Пример.
Рассчитайте доходность процентного векселя, если известно, что цена приобретения векселя составляет 55000 руб., цена погашения векселя 57000 руб., до погашения векселя осталось 60 дней.
Решение.
![]()
Литература
1. Анесянц С.А. Основы функционирования рынка ценных бумаг. – М.: «Финансы и статистика», 2005.
2. Бердникова Т.Б. Оценка ценных бумаг. – М.: ИНФРА-М, 2003.
3. Бердникова Т.Б. Рынок ценных бумаг и биржевое дело. – М.: ИНФРА-М, 2002.
4. Биржевое дело: Учебник / Под ред. В.А. Галанова, А.И. Басова. – М.: Финансы и статистика, 2003.
5. Боровкова В.А. Рынок ценных бумаг. – СПб.: Питер, 2005.
6. Гинзбург А.И., Михейко М.В. Рынки валют и ценных бумаг. – СПб.: Питер, 2004.
7. Дегтярева О.И., Коршунов Н.М., Жуков Е.Ф. Рынок ценных бумаг и биржевое дело. – М.: «ЮНИТИ», 2002.
8. Жуков Е.Ф. Ценные бумаги и фондовые рынки. – М.: ЮНИТИ, 1998.
9. Килячков А.А., Чалдаева Л.А. Практикум по российскому рынку ценных бумаг. – М.: БЕК, 1997.
10. Килячков А.А., Чалдаева Л.А. Рынок ценных бумаг и биржевое дело. – М.: «Экономистъ», 2004.
11. Миркин Я.М. Ценные бумаги и фондовый рынок. – М.: Перспектива, 1997.
12. Рынок ценных бумаг / Под ред. В.А. Галанова, А.И. Басова. – М.: Финансы и статистика, 2004.
13. Рынок ценных бумаг: Учебник Под ред. В.И. Колесникова, В.С. Торкановского. - М.: Финансы и статистика, 1999.
14. Чалдаева Л.А. Фондовая биржа. Организационно-управленческие структуры. – М.: 2002.
15. Информационные материалы, размещенные в сети Интернет.