зно математика 2007 с ответами
СОДЕРЖАНИЕ: МАТЕМАТИКА ТЕСТОВІ ЗАВДАННЯ 2007 РОКУ З ВІДПОВІДЯМИ ТА КОМЕНТАРЯМИ Тест зовнішнього незалежного оцінювання з математики перевіряє: відповідність знань, умінь і навичок учнів програмовим вимогам;МАТЕМАТИКА
ТЕСТОВІ ЗАВДАННЯ 2007 РОКУ З ВІДПОВІДЯМИ ТА КОМЕНТАРЯМИ
Тест зовнішнього незалежного оцінювання з математики перевіряє:
· відповідність знань, умінь і навичок учнів програмовим вимогам;
· рівень навчальних досягнень учнів;
· ступінь підготовленості випускників загальноосвітніх навчальних
закладів до подальшого навчання у вищих навчальних закладах.
При укладанні тесту були використані підручники та посібники, рекомендовані Міністерством освіти і науки України для класів універсального, природничого, фізико-математичного профілів, а також для класів, шкіл, ліцеїв і гімназій математичного профілю та для спеціалізованих шкіл і класів з поглибленим вивченням математики.
Частина 1
ЗАВДАННЯ З ВИБОРОМ ОДНІЄЇ ПРАВИЛЬНОЇ ВІДПОВІДІ
- Розташуйте у порядку спадання числа
| А | Б | В | Г | Д |
Правильна відповідь: А.
Компоненти програмових вимог, що перевіряються завданням: Дійсні числа. Порівняння чисел. Основна логарифмічна тотожність.
- Банк сплачує своїм вкладникам 8% річних. Визначте, скільки грошей треба покласти на рахунок, щоб через рік отримати 60 грн. прибутку.
| А | Б | В | Г | Д |
| 1150 | 1050 | 950 | 850 | 750 |
Правильна відповідь: Д.
Компоненти програмових вимог, що перевіряються завданням: Задачі на відсотки.
- З натуральних чисел від 1 до 30 учень навмання називає одне. Яка ймовірність того, що це число є дільником числа 30?
| А | Б | В | Г | Д |
Правильна відповідь: В.
Компоненти програмових вимог, що перевіряються завданням: Поняття ймовірності випадкової події.
- Розв’яжіть нерівність
| А | Б | В | Г | Д |
Правильна відповідь : Д.
Компоненти програмових вимог, що перевіряються завданням: Дробово-раціональні нерівності.
- Знайдіть область визначення функції
| А | Б | В | Г | Д |
Правильна відповідь : Г.
Компоненти програмових вимог, що перевіряються завданням: Властивості елементарних функцій: область визначення.
- Будівельна компанія закупила для нового будинку металопластикові вікна та двері у відношенні 4:1. Укажіть число, яким може виражатися загальна кількість вікон та дверей в цьому будинку.
| А | Б | В | Г | Д |
| 41 | 45 | 54 | 68 | 81 |
Правильна відповідь : Б.
Компоненти програмових вимог, що перевіряються завданням: Застосування ознак подільності чисел до розв’язування задач.
- Обчисліть
| А | Б | В | Г | Д |
| 1 | 2 |
Правильна відповідь : Д.
Компоненти програмових вимог, що перевіряються завданням: Тотожні перетворення і знаходження значень виразів, що містять тригонометричні функції.
- Розв’яжіть рівняння tg
| А | Б | В | Г | Д |
| інша відповідь |
Правильна відповідь : Г.
Компоненти програмових вимог, що перевіряються завданням: Розв’язування найпростіших тригонометричних рівнянь.
9.
За видом графіка функції у
= кх
+ b
визначте знаки коефіцієнтів к
і b
.
Оберіть правильне твердження.

| А | Б | В | Г | Д |
Правильна відповідь : Г.
Компоненти програмових вимог, що перевіряються завданням: Лінійна функція та її властивості.
- Укажіть парну функцію.
| А | Б | В | Г | Д |
Правильна відповідь : Д.
Компоненти програмових вимог, що перевіряються завданням: Властивості елементарних функцій: парність.
- Обчисліть
| А | Б | В | Г | Д |
Правильна відповідь : А.
Компоненти програмових вимог, що перевіряються завданням: Властивості логарифма.
- Розв’яжіть нерівність
| А | Б | В | Г | Д |
| (0; 10) | (0,1; 10) | (10; 0) |
Правильна відповідь : Б.
Компоненти програмових вимог, що перевіряються завданням: Розв’язування найпростіших логарифмічних нерівностей, використовуючи властивості логарифмічної функції.
- Розв’яжіть рівняння
| А | Б | В | Г | Д |
Правильна відповідь : Г.
Компоненти програмових вимог, що перевіряються завданням: Розв’язування найпростіших показникових рівнянь.
- Укажіть, скільки дійсних коренів має рівняння
| А | Б | В | Г | Д |
| жодного | один | два | три | більше трьох |
Правильна відповідь : В.
Компоненти програмових вимог, що перевіряються завданням: Розв’язування рівнянь з модулем.
- Знайдіть первісну функції
| А | Б | В | Г | Д |
Правильна відповідь : Б.
Компоненти програмових вимог, що перевіряються завданням: Первісна. Основна властивість первісної. Правила знаходження первісних.
16.
На рисунку зображений графік функції ![]() та дотичні до нього в точках
та дотичні до нього в точках ![]() та
та ![]() . Користуючись геометричним змістом похідної, знайдіть
. Користуючись геометричним змістом похідної, знайдіть ![]() .
.
![]()
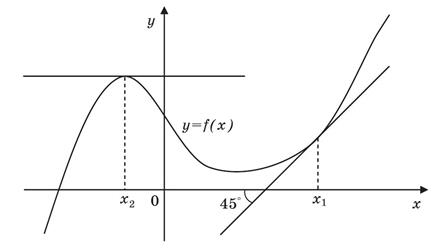
| А | Б | В | Г | Д |
| 1 |
Правильна відповідь : А.
Компоненти програмових вимог, що перевіряються завданням: Геометричний зміст похідної.
- Градусна міра зовнішнього кута А
рівнобедреного трикутника АВС (АВ = ВС)
становить
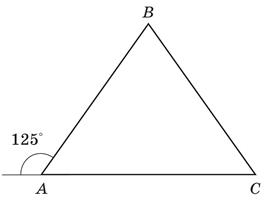
| А | Б | В | Г | Д |
| 30о | 40о | 50о | 60о | 70о |
Правильна відповідь : Д.
Компоненти програмових вимог, що перевіряються завданням: Властивість рівнобедреного трикутника. Сума кутів трикутника. Градусна міра кута.
- Точка М
– середина сторони квадрата АВС
D
. Площа зафарбованої частини дорівнює 7
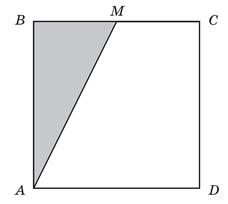
| А | Б | В | Г | Д |
| 14 |
21 |
28 |
35 |
42 |
Правильна відповідь : В.
Компоненти програмових вимог, що перевіряються завданням: Властивості квадрата. Площі рівних фігур.
- Знайдіть координати точки М
, відносно якої симетричні точки
| А | Б | В | Г | Д |
| інша відповідь |
Правильна відповідь : А.
Компоненти програмових вимог, що перевіряються завданням: Координати точки та симетрія відносно точки у просторі.
- Знайдіть об’єм тіла, утвореного обертанням круга навколо свого діаметра, довжина якого дорівнює а см
.
| А | Б | В | Г | Д |
Правильна відповідь : Г.
Компоненти програмових вимог, що перевіряються завданням: Знаходження об’єму тіла обертання.
Частина 2
ЗАВДАННЯ ВІДКРИТОЇ ФОРМИ З КОРОТКОЮ ВІДПОВІДДЮ
- Обчисліть
Правильна відповідь : ![]() .
.
Компоненти програмових вимог, що перевіряються завданням: Дії над ірраціональними числами.
- Знайдіть суму перших дванадцяти непарних натуральних чисел.
Правильна відповідь : 144.
Компоненти програмових вимог, що перевіряються завданням: Сума членів арифметичної прогресії.
- Укажіть найменше ціле число, яке є розв’язком нерівності
Правильна відповідь : ![]() .
.
Компоненти програмових вимог, що перевіряються завданням: Розв’язування раціональних нерівностей методом інтервалів.
- На перегоні, довжина якого дорівнює
10 ![]() менше, ніж мала бути за розкладом, і запізнився на 48
менше, ніж мала бути за розкладом, і запізнився на 48 ![]() . З якою швидкістю мав рухатися поїзд за розкладом?
. З якою швидкістю мав рухатися поїзд за розкладом?
Правильна відповідь : 60 ![]()
Компоненти програмових вимог, що перевіряються завданням: Розв’язування текстових задач за допомогою рівняння або системи рівнянь.
- Обчисліть
Правильна відповідь : 0,5
Компоненти програмових вимог, що перевіряються завданням: Тотожні перетворення і знаходження значень тригонометричних виразів.
- Розв’яжіть рівняння
Правильна відповідь : 11 (або 8).
Компоненти програмових вимог, що перевіряються завданням: Розв’язування ірраціональних рівнянь.
Примітка. Враховуючи, що чинні підручники з математики для загальноосвітніх навчальних закладів по-різному тлумачать ситуацію, коли рівняння мають кратні корені, відповідь 8 також є правильною.
Розв’язання.
Знайдемо область визначення: ![]()
![]()
![]()
Рівняння ![]() рівносильне сукупності рівнянь:
рівносильне сукупності рівнянь:
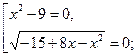 звідси:
звідси: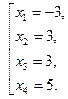
Рівняння має чотири корені, з яких два рівні між собою. Корінь ![]() не входить в область визначення. Тому 3+3+5=11.
не входить в область визначення. Тому 3+3+5=11.
- Розв’яжіть систему рівнянь
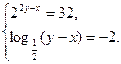
Запишіть у відповідь добуток ![]() , якщо пара
, якщо пара ![]() є розв’язком вказаної системи рівнянь.
є розв’язком вказаної системи рівнянь.
Правильна відповідь : ![]()
Компоненти програмових вимог, що перевіряються завданням: Розв’язування систем рівнянь, у яких одне рівняння показникове, а інше логарифмічне.
- Середній вік одинадцяти футболістів команди становить 22 роки. Під час гри одного з футболістів було вилучено з поля, після чого середній вік гравців, що залишилися, став 21 рік. Скільки років футболісту, який залишив поле?
Правильна відповідь : 32.
Компоненти програмових вимог, що перевіряються завданням: Статистичні характеристики рядів даних: середнє значення випадкової величини.
- Обчисліть
Правильна відповідь : 4.
Компоненти програмових вимог, що перевіряються завданням: Тотожні перетворення логарифмічних виразів.
- Знайдіть найбільше ціле значення параметра а
, при якому система рівнянь
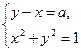 має два розв’язки.
має два розв’язки.Правильна відповідь : 1.
Компоненти програмових вимог, що перевіряються завданням: Розв’язування систем рівнянь з параметрами графічно.
- Знайдіть найбільше значення функції
Правильна відповідь : 2.
Компоненти програмових вимог, що перевіряються завданням: Дослідження функції за допомогою похідної.
- Знайдіть найменше ціле значення параметра а
, при якому рівняння
Правильна відповідь : ![]()
Компоненти програмових вимог, що перевіряються завданням: Розв’язування рівнянь з параметрами.
- Сторона рівностороннього трикутника АВС
дорівнює 5 см. Знайдіть скалярний
добуток ![]() .
.
Правильна відповідь : 12,5.
Компоненти програмових вимог, що перевіряються завданням: Скалярний добуток векторів.
- Для опалювальної системи будинку необхідні радіатори із розрахунку: три одиниці на 50м3
. Яку кількість одиниць радіаторів треба замовити, якщо новий будинок має форму прямокутного паралелепіпеда розміру 15м18м25м?
Правильна відповідь : 405.
Компоненти програмових вимог, що перевіряються завданням: Задачі прикладного змісту на знаходження об’єму фігур: об’єм прямокутного паралелепіпеда.
35
. Апофема правильної чотирикутної піраміди дорівнює 2![]() см
і нахилена під кутом
см
і нахилена під кутом ![]() до площини основи. Знайдіть об’єм піраміди.
до площини основи. Знайдіть об’єм піраміди.
Правильна відповідь : 12 ![]() .
.
Компоненти програмових вимог, що перевіряються завданням: Знаходження об’єму фігури, використовуючи теореми планіметрії: об’єм піраміди.
Частина 3
ЗАВДАННЯ ВІДКРИТОЇ ФОРМИ З РОЗГОРНУТОЮ ВІДПОВІДДЮ
36. У правильній чотирикутній піраміді SABCD ( S – вершина) бічне ребро вдвічі більше сторони основи. Знайдіть кут між медіаною трикутника SDC , проведеною з вершини D , та середньою лінією трикутника ASC , що паралельна основі піраміди.
Правильна відповідь : ![]() .
.
Розв’язання (авторський варіант)
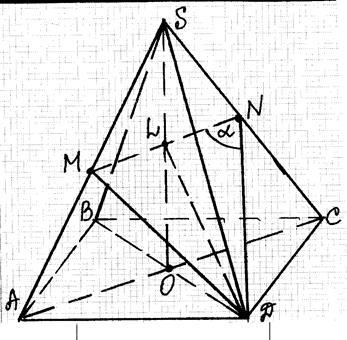
Нехай SABCD – задана правильна піраміда, в основі якої лежить квадрат ABCD, і SO її висота. Позначимо сторону основи АВ через а , тоді бічне ребро SA = 2a .
У трикутнику SDC
з вершини D
проведемо медіану DN,
N
– середина ребра SC
. У трикутнику ASC
проведемо середню лінію, паралельну AC
. Вона перетинає ребра SA
та SC
у точках М
та N
відповідно, AM =
MS
та SN =
NC
(за означенням середньої лінії). Оскільки АС
лежить у площині ABC
і MN
|| AC
, то MN
|| (ABC
). Прямі MN
та ND
перетинаються в точці N
, тому кут MND
є шуканим кутом між медіаною DN
трикутника SDC
і середньою лінією MN
трикутника ASC
. Позначимо ![]() .
.
Діагональ АС
квадрата АВС
D
дорівнює ![]() , тому середня лінія MN
=
, тому середня лінія MN
= ![]() .
.
Висота SO
піраміди перетинає MN
в точці L
. Оскільки трикутники ASC
і SMN
є рівнобедреними, то АО = ОС
і ML =
LN
= ![]() .
.
З прямокутного трикутника ![]()
![]() .
.
За теоремою Фалеса SL =
LO
= ![]() SO
=
SO
= ![]() .
.
З прямокутного трикутника ![]()
![]() .
.
Трикутник DNM рівнобедрений, оскільки DM = DN як медіани рівних трикутників SAD та SCD . Медіана DL є висотою. Отже, трикутник DLN є прямокутним.
З трикутника DLN маємо:
![]() .
.
Відповідь. ![]() .
.
Схема оцінювання
1. За правильно побудований рисунок до задачі з обґрунтуванням паралельності відповідної середньої лінії до основи учень одержує 1 бал .
2. За обгрунтування рівності двох сторін трикутника MND ( DM= DN) учень одержує ще 1 бал .
3. Якщо учень правильно знайшов елементи трикутника DLN
, необхідні для знаходження кута ![]() , він одержує ще 1 бал
.
, він одержує ще 1 бал
.
4. За правильну відповідь учень одержує ще 1 бал .
Таким чином, за правильно розв’язану задачу учень одержує 4 бали .
· Якщо учень не з’єднує точки М
і Д
на рисунку, а розглядає кут ![]() як кут трикутника DLN,
то в цьому випадку треба обґрунтувати, що трикутник DLN –
прямокутний.
Тоді має місце така схема оцінювання
:
як кут трикутника DLN,
то в цьому випадку треба обґрунтувати, що трикутник DLN –
прямокутний.
Тоді має місце така схема оцінювання
:
1. За правильно побудований рисунок до задачі з обґрунтуванням паралельності відповідної середньої лінії до основи учень одержує 1 бал .
2. За обґрунтування того, що ![]() учень одержує ще 1 бал
.
учень одержує ще 1 бал
.
3. Якщо учень правильно знайшов елементи трикутника DLN
, необхідні для знаходження кута ![]() , він одержує ще 1 бал
.
, він одержує ще 1 бал
.
4. За правильну відповідь учень одержує ще 1 бал .
Таким чином, за правильно розв’язану задачу учень одержує 4 бали .
· Якщо учень для розв’язування задачі використав векторно-координатний метод, то тоді має місце така схема оцінювання :
1. За правильне обґрунтування висоти SO учень одержує 1 бал .
2. За вибір системи координат з поясненням необхідних точок учень одержує ще 1 бал .
3. За обчислення координат цих точок учень одержує ще 1 бал .
4. За правильну відповідь учень одержує ще 1 бал .
Таким чином, за правильно розв’язану задачу учень одержує 4 бали .
37. Побудуйте графік функції 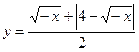 .
.
Розв’язання
Знаходимо область визначення функції, тобто розв’язуємо нерівність ![]() Отже,
Отже, ![]() .
.
Знайдемо точки, у яких модуль обертається в нуль, тобто розв’яжемо рівняння ![]() , звідки
, звідки ![]() .
.
Якщо ![]() , то
, то ![]() .
.
Якщо ![]()
![]() , то
, то ![]() .
.
Побудуємо ескіз графіка вказаної функції.
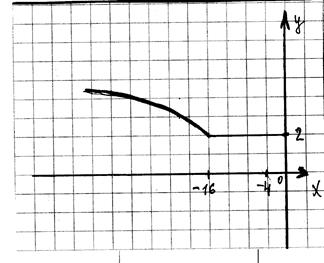
Схема оцінювання
1. За правильно знайдене ![]() учень одержує 1 бал
.
учень одержує 1 бал
.
2. Якщо учень правильно розкрив модуль на проміжку ![]() , то він одержує 1 бал
.
, то він одержує 1 бал
.
3. Якщо учень правильно розкрив модуль на проміжку ![]() , то він одержує ще 1 бал
.
, то він одержує ще 1 бал
.
4. За правильно побудований ескіз графіка вказаної функції учень одержує ще 1 бал .
Тобто за правильно розв’язане завдання учень одержує 4 бали .
38. Розв’яжіть нерівність
![]() .
.
Правильна відповідь: при ![]()
![]() ;
;
при ![]()
![]() ;
;
при ![]()
![]() .
.
Розв’язання
Визначимо область допустимих значень параметра а
: ![]() .
.
Дана нерівність еквівалентна наступній сукупності систем нерівностей:
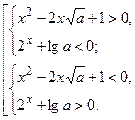
Розв’яжемо спочатку першу систему.
Розглянемо нерівність ![]() .
.
![]() .
.
- Якщо
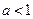 , то розв’язком першої нерівності даної системи буде
, то розв’язком першої нерівності даної системи буде 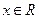 . Тоді розв’язком нерівності
. Тоді розв’язком нерівності 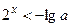 буде
буде 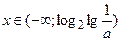 при
при 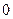
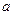 1. Тобто, розв’язок першої системи матиме вигляд
1. Тобто, розв’язок першої системи матиме вигляд 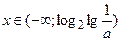 при
при 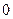
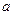 1.
1. - Якщо
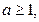 то розв’язком нерівності
то розв’язком нерівності 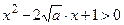 буде
буде 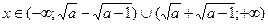 , а нерівність
, а нерівність 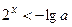 не має розв’язків. Отже, перша система не має розв’язків.
не має розв’язків. Отже, перша система не має розв’язків.
Розв’яжемо другу систему.
Розглянемо нерівність ![]() .
.
Ураховуючи розв’язання попередньої системи, ![]() .
.
1. Якщо ![]() , то нерівність не має розв’язків. Отже, друга система не має розв’язків.
, то нерівність не має розв’язків. Отже, друга система не має розв’язків.
2. Якщо ![]() то розв’язком нерівності
то розв’язком нерівності ![]() буде
буде ![]() . Тоді розв’язком нерівності
. Тоді розв’язком нерівності ![]() буде
буде ![]() . Тобто розв’язок другої системи матиме вигляд
. Тобто розв’язок другої системи матиме вигляд ![]() .
.
3. Якщо ![]() , то одержимо нерівність
, то одержимо нерівність ![]() , звідси
, звідси ![]() .
.
Отже, загальна відповідь: при ![]()
![]() ;
;
при ![]()
![]() ;
;
при ![]()
![]() .
.
Схема оцінювання
- Якщо учень правильно знайшов область допустимих значень параметра а і розглянув нерівність як сукупність двох систем, то він одержує 1 бал .
- За правильно розв’язану першу систему нерівностей учень одержує ще 2 бали . Якщо він припустився помилки при розв’язанні однєї з нерівностей при умові, що друга нерівність розв’язана правильно, учень одержує 1 бал .
- За правильно розв’язану другу систему нерівностей учень одержує ще 2 бали . Якщо він припустився помилки при розв’язанні однєї з нерівностей при умові, що друга нерівність розв’язана правильно, учень одержує 1 бал .
- За правильно записану відповідь учень одержує ще 1 бал .
Тобто за правильно розв’язану задачу учень одержує 6 балів .
· Якщо учень розв’язує нерівність методом інтервалів , то в цьому випадку має місце така схема оцінювання:
- За правильно знайдене ОДЗ змінної і параметра учень одержує 1 бал .
- За правильно знайдені нулі функції
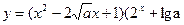 ) з вказівкою відповідних значень параметра учень одержує 2 бали
.
) з вказівкою відповідних значень параметра учень одержує 2 бали
.
Якщо знайдені нулі тільки одного множника з вказівкою відповідних значень параметра, то учень одержує лише 1 бал .
- За правильне застосування методу інтервалів на кожному з виділених проміжків для параметра а
учень одержує 2 бали
.
Якщо учень розглянув один з випадків ![]() або
або ![]() , то він одержує лише 1 бал
.
, то він одержує лише 1 бал
.
- За правильно записану відповідь учень одержує ще 1 бал
.
Тобто за правильно розв’язану задачу учень одержує 6 балів .
· Якщо учень розв’язує нерівність методом розбиття усіх значень а на три випадки:
![]() , а=
1,
, а=
1, ![]() ,
то в цьому випадку має місце така схема оцінювання:
,
то в цьому випадку має місце така схема оцінювання:
- Якщо учень дослідив випадок
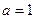 і одержав відповідь, то він одержує1 бал.
і одержав відповідь, то він одержує1 бал.
- Якщо учень дослідив випадок
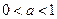 і одержав відповідь, то він одержує2 бали.
і одержав відповідь, то він одержує2 бали.
- Якщо учень дослідив випадок
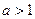 і одержав відповідь, то він одержує2 бали.
і одержав відповідь, то він одержує2 бали.
- За правильно записану відповідь учень одержує ще 1 бал .
Тобто за правильно розв’язану задачу учень одержує 6 балів .