Строение конечной группы 24-го порядка, заданной образующими и определяющими соотношениями G
СОДЕРЖАНИЕ: Московский Государственный Институт Электронной Техники (Технический Университет) Курсовая работа По дисциплине: Дискретная Математика Тема: «Строение конечной группы 24-го порядка, заданной
![]()
 |
|
Московский Государственный Институт
Электронной Техники
(Технический Университет)
Курсовая работа
По дисциплине:
« Дискретная Математика »
Тема:
«Строение конечной группы 24-го порядка, заданной
образующими и определяющими соотношениями
G = x, y | x2 =y2 =(xy)3 »
Выполнил: .
Группа: ЭКТ-35
Проверил: Клюшин А.В.
Москва 2009г.
Оглавление.
Титульный лист…………………………………………………………….1
Оглавление………………………………………………………………...2
1. Теоретическая часть…………………………………………………...3
1.1 Понятие группы……………………………………………………3
1.2 Определение группы. Свойства подгрупп………………………4
1.3 Изучения строения групп, заданных образующими и определяющими соотношениями……………………………….....5
2. Практическая часть…………………………………………………….7
2.1 Доказательство того, что в группе nэлементов………………..7
2.2 Оперделения порядка элементов…………………………………9
2.3 Вычисление таблицы умножения данной группы.
Нахождение центра группы………………………………………10
2.4 . Составление таблицы подгрупп, порожденных
двумя элементами………………………………………………………11
2.5 Нахождение всех подгрупп группы G…………………………………13
2.6 Структура всех подгрупп……………………………………………….14
3. Список используемой литературы…………………………………..……..15
.
1. Теоретическая часть.
1.1. Понятие группы.
Определение 1. Пусть G — некоторое множество. Бинарной операцией на G
называется произвольное отображение G G ® G. Если (g1,g2)G 1 G 2 , то
результат бинарной операции чаще всего будем обозначать g 1 • g 2 , где (•) — знак
бинарной операции.
Определение 2. Множество G с бинарной операцией (•) называется группой, если
1) g1 , g2,g3 G (g1• g2) • g3 =g1• ( g2• g3)
2) $ e G: e •g = g •е = e, этот элемент е будем называть единицей группы G;
3) g G $ g-1 G : g • g -1 = g -1 • g = e, элемент g -1 для элемента g будем
называть обратным к g.
Если к условиям 1)-3) добавить условие
4) g1 , g2 G g1•g2 = g2•g1 ,то группа G называется абелевой или коммутативной.
В этом случае знак бинарной операции чаще обозначают (+), что мы и будем
делать.
Результат бинарной операции (•) в дальнейшем будем называть произведением.
Прежде всего заметим, что, благодаря условию 1), произведение нескольких
элементов группы можно записывать без скобок.
Определение 3. Центр группы G, обычно обозначается Z(G), определяется как
Z(G) = {g G | gh = hg для любого h G } .
Иначе говоря, это максимальная подгруппа элементов, коммутирующих с каждым
элементом G.
Предложение 1. Единица в группе может быть только одна.
Доказательство. Действительно, если два элемента e1,e2 G обладают свойством
2), то e1 =e1 • е2 = e2 • e1
Предложение доказано.
Предложение 2. В группе элемент, обратный к данному элементу g, может быть
только один.
Доказательство. Если два элемента g -1
1 и g -1
2 обладают свойством 3) для элемента
g, то
g 1
-1 = g 1
-1 • e= g 1
-1 •g • g 2
-1 = e • g 2
-1 = g 2
-1
Что и требовалось доказать.
Каждая конечная группа может быть задана таблицей умножения, которая иначе
называется таблицей Кэли.
Для составления таблицы Кэли элементы группы выписываются по горизонтали и
вертикали в определенном порядке. В клетке на пересечении строки g G и
столбца h G пишется элемент gh.
Таблица Кэли обладает важным свойством: в каждой строке и каждом столбце
каждый элемент группы встречается ровно один раз. Таким образом, каждый
столбец и каждая строка являются некоторой перестановкой элементов группы.
1.2. Определение подгруппы. Свойства подгрупп.
Определение 1. Подмножество H группы G называется подгруппой, если
выполнены следующие условия
1) е H;
2) h1 , h2 H h1 • h2 H;
3) h H h-1H.
Как мы уже знаем, каждую конечную группу можно задать с помощью таблицы
умножений или таблицы Кэли. В каждой строке и каждом столбце таблицы Кэли
каждый элемент группы встречается ровно один раз. Если элементы группы
перенумеровать, то каждому элементу будет соответствовать некоторая
перестановка.
Определение 2. Если H - подгруппа группы G и g G, то множество gH = { gh | h
H}
называется левым смежным классом группы G по подгруппе H. Соответственно,
множество Нg называется правым смежным классом.
Каждое разбиение группы G на левые (правые) смежные классы по любой
подгруппе H задает некоторое отношение эквивалентности.
Определение 3. Число элементов конечной группы или, соответственно,
подгруппы будем называть ее порядком.
Определение 4. Пусть а 1 ,… ,а n G. Через а 1 ,… ,а n будем обозначать
наименьшую подгруппу в G, содержащую элементы а 1 ,… ,а n . Если а 1 ,… ,а n = G,
то элементы {а 1 ,… ,а n } будем называть системой образующих группы G. Систему
{а 1 ,… ,а n } будем называть минимальной системой образующих группы G, если
после удаления любого элемента оставшееся множество уже не будет являться
системой образующих для G. Группу G будем называть циклической, если
найдется элемент g G такой, что g=G.
Теорема 2 (Лагранжа). Порядок подгруппы делит порядок конечной группы.
Доказательство. Пусть G — конечная группа, Н — подгруппа. Рассмотрим
разбиение группы G на левые смежные классы по подгруппе Н. Во-первых, всегда
g gH. Значит, объединение всех левых смежных классов дает G.
Далее, покажем, что левые смежные классы либо не пересекаются, либо
совпадают. Действительно, если g3 g1H g2H, то g 3 = g 1 h 1 = g 2 h 2 для некоторых
h 1 , h 2 H. Но тогда g1 = g 2 h 2 h 1
-1 g2H, а g 2 =g 1 h 1 h 2
-1 g1H. Отсюда следует, что g 1 H
= g 2 Н.
Теперь покажем, что все левые смежные классы состоят из одного и того же числа
элементов. Действительно, рассмотрим отображение H ® gH, задаваемое правилом
g ® gh. Разные элементы при этом отображении переходят в разные.
Действительно, если gh1= gh 2 , то, умножая равенство слева на g -1 , получим h 1 = h 2 .
Следовательно, |Н| = |gН|. Таким образом, конечное множество G разбилось на
некоторое множество (пусть к) подмножеств, состоящих из |Н| элементов. Тогда
|G| = к •|Н|.
Теорема доказана.
Следствие. Если G - конечная группа, то порядки ее элементов являются
делителями числа |G|.
Доказательство. Если о(g) == к, то множество {g, g 2 ,... , gk-1, е} образует подгруппу в
G. Следствие доказано.
1.3 Изучение строения групп, заданных образующими и определяющими
соотношениями.
Рассмотрим алфавит из символов х, у, х -1 , у -1 . Конечную последовательность
символов будем называть словом. Если z - символ, договоримся записывать z n
вместо {
n
z...z . Слово, состоящее из пустого множества символов будем обозначать
е . Кроме того, если n,m - целые числа разных знаков, то слово z n z m договоримся
сокращать и записывать как z n+m . Например, х 3 х -4 = х -1 , х 2 х -2 = е .
На множестве слов рассмотрим бинарную операцию (·) , которую будем на-
зывать умножением. Если u=z 1 ...z n и v = t 1 …t m - два слова, то их произведением
будем называть слово uv = z 1 ...z n t 1 ...t m , в котором произведены все возможные
сокращения. Если одно из слов равно е , то положим е·u = u·е = u . Несложно
видеть, что данная бинарная операция ассоциативна, а элемент е является
единицей. Кроме того, каждое слово имеет обратное. Действительно, если u =
z 1 ...z n , то u -1 = 1 1
n 1 z - ...z - .
Таким образом, множество всех слов в данном алфавите с определенной
выше бинарной операцией будет группой. Эта группа называется свободной
группой с двумя образующими х, у .
Аналогично можно определить свободную группу с тремя образующими и
т.д.
Пусть F - свободная группа с образующими x 1 ...x n . Равенство двух слов u=v
будем называть соотношением. Всякое соотношение можно записать в виде u·v -1 =
е . Пусть задана система из k соотношений
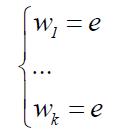 (1)
(1)
Рассмотрим все нормальные подгруппы группы F , содержащие слова w 1 ,...,
w k Одной из таких подгрупп является сама группа F. Пересечение всех нормальных
подгрупп, содержащих w 1 ,..., w k , обозначим N . Можно показать, что пересечение
нормальных подгрупп всегда будет являться нормальной подгруппой. Таким
образом, N будет наименьшей нормальной подгруппой, содержащей элементы
w 1 ,..., w k . Пусть G = F/N - фактор-группа. Напомним, что элементами фактор-
группы являются смежные классы по подгруппе N . Если u - слово, u F, то через
u будем обозначать смежный класс, содержащий u . Тогда в фактор-группе G
справедливы равенства 1 w = k w = 1 . Группу G будем называть группой с
образующими x 1 ...x n и соотношениями (1) и задавать в следующем виде
1 n 1 1 k k G=x ,...,x | u = v ,...,u = v
(2)
На практике в каждом смежном классе группы G = F/N выбирают наиболее
простое слово. Если одно слово группы F можно получить из другого с
помощью алгебраических преобразований, используя соотношения (1), то в группе
G такие слова равны (точнее, они лежат в одном смежном классе).
В дальнейшем мы ограничимся рассмотрением только конечных групп, за-
данных образующими и соотношениями. Поскольку в конечной группе каждый
элемент имеет конечный порядок, можно ограничиться словами, в которые каждый
6
символ входит в неотрицательной степени. Действительно, если , х n = 1 (n 1), то х
-1 = х n- 1.
На множестве слов введем порядок. Сначала упорядочим множество ис-
ходных символов, т.е. будем считать, что x 1 x 2 ... x n . В слове
1 k
1 k u = t a ...t a можно предполагать, что следующий символ отличен от предыдущего,
т.е. i 1 i t t + . Пусть имеются два слова 1 k
1 k u = t a ...t a и 1 m
1 m v = s b ... s b , где i i t , s { x 1 ... x n }.
Будем считать, что u v , если 1 k 1 m a + ... +a b + ... + b . В случае
1 k 1 m a + ... +a = b + ... + b будем считать, что u v , если 1 1 t s или 1 1 t = s , но
1 1 a b . Если 1 1 t = s и 1 1 a = b , то для сравнения слов u и v надо рассмотреть
следующие символы и т.д..
Таким образом, в алфавите х, у получается следующая последовательность
слов, расположенных по возрастанию.
1, x, y, x 2 ,xy, yx, y 2 ,x 3 ,x 2 y,xyx,xy 2 , yx 2 , yxy, y 2 x, y 3 ,...
Имея задание группы в виде (2), прежде всего нужно убедиться, что в G
лишь конечное число элементов. Используя соотношения (1) нужно в каждом
смежном классе выбрать наименьшее слово. Это иногда является непростой
задачей, т.к. не существует алгоритма позволяющего определить, являются ли два
слова равными в силу соотношений (1).
Центром группы называется множество всех ее элементов, коммутирующих
со всеми элементами группы. Центр группы G является подгруппой и обозначается Z(G) . Если имеется таблица умножений, то центр образуют те элементы, для
которых соответствующая строка в таблице умножений равна столбцу с тем же
номером.
2. Практическая часть
Рассмотрим группу G с образующими элементами x и y, введенной
бинарной операцией (), которую будем называть умножением.
G= x, y| x 2 = y 2 =( xy )3 , n = 24.
По определению группы операция умножения ассоциативна, а элемент e
является единицей, и для нее справедливы известные соотношения. Минимальной
системой образующих для нашей группы будет являться система из двух
элементов - {x, y}. Определим единицу данной группы.
xy = yxyx y 2 =( yxyxxyxy ) xy , yxyxxyxy = e , x 8 = y 8 = e
2.1. Доказательство того, что в группе n элементов.
Путем анализа определяющих соотношений убедиться, что число
элементов этой группы действительно равно n. Выразить все элементы
через образующие.
Рассмотрим каждый элемент группы в виде слова, записанного с помощью букв x и
y. Будем для начала рассматривать слова длины 1, т.е. элементы x и y. Путем
дописывания справа от имеющегося слова букв x или y, будем получать слова
длины на единицу больше, чем данное. Новое слово будем пытаться свести к уже
имеющимся с помощью определяющих соотношений: x 8 = e , y 8 = e , x 2 = y 2 =( xy )3 .
Если нам это удается, то для полученного “старого” слова
процесс прекращаем, иначе продолжаем действовать по той же схеме, т.е.
дописываем буквы и пытаемся свести полученное слово к уже имеющимся. В
итоге, каждое неприводимое слово будет новым элементом группы.
1. e
2. x
3. y
4. x2
5. xy= x2 yxyx
6. yx= x3 yxy
7. x3
8. x2 y =y x2 = y3
9. xyx
10. x y2 = y2 x
11. yxy= x5 yx= x3 yx y2
12. x4 =x y2 x= x2 y2
13. x3 y= x y3 =xy x2
14.x2 yx= yx y2 = y3 x=y x3
15. xyxy=yxyx
16. x5 = x3 y2
17. x4 y = x2 y x2
18. x3 y x=xyx y2
19. x2 y xy=yxy x2
20. x6 = x4 y2
21. x5 y = x3 y x2 = x4 yxy
22. x4 yx= x2 yx y2
23. x7 = x5 y2
24. x6 y = x4 y x2
Данным методом мы доказали, что в нашей группе действительно 24 элемента.
1. e
2. x
3. y
4. x2
5. xy
6. yx
7. x3
8. x2 y
9. xyx
10.x y2
11.yxy
12.x4
13.x3 y
14.x2 yx
15.xyxy
16.x5
17.x4 y
18.x3 y x
19.x2 y xy
20.x6
21.x5 y
22. x4 yx
23. x7
24. x6 y
2.2 Определение порядков элементов.
1. o(e)=1
2. o(x)=8
3. o(y)=8
4. o(x2 )=4 x2 x2 x2 x2 =e
5. o(xy)=12
6. o(yx)=12
7. o(x3 )=4
8. o(x2 y )=4
9. o(xyx )=8
10.o(yxy )=8
11.o(x 4 )=2
12.o(x 3 y )=8
13.o(x 2 yx )=4
14.o(xyxy)=6
15.o(yxyx)=4
16.o(x 5 )=8
17.o(x 4 y)=8
18.o(x 3 y x )=8
19.o(x 2 y xy )=8
20.o(x 6 )=4
21.o(x 5 y )=8
22.o(x 4 yx )=4
23.o(x 7 )=8
24.o(x 6 y )=4
В соответствие с полученными результатами переобозначим элементы группы:
| Обозначение | H1 | H2 | C1 | L1 | L2 | C2 | C3 | H3 | c4 | H4 | A1 | H5 | C5 | F1 | H6 |
| Элемент | x | y | x2 | xy | yx | x3 | x2 y | xyx | yxyx | yxy | x 4 | x 3 y | x 2 yx | xyxy | x 5 |
| Обозначение | H7 | H8 | H9 | C6 | H10 | C7 | H11 | C8 |
| Элемент | x 4 y | x 3 y x | x 2 y xy | x 6 | x 5 y | x 4 yx | x 7 | x 6 y |
2.3. Вычисление таблицы умножений данной группы. Нахождение центра группы.
Ввиду большого количества громоздких вычислений, не будем приводить их.
Скажем только то, что они основываются на базовых соотношениях x 8 = e , y 8 = e ,
x 2 = y 2 =( xy )3 , а также на ряде производных соотношений.
Применяя эти рассуждения, получим таблицу умножений. Приведем все полученные элементы, а затем рассмотрим примеры их получения:
| e | a1 | C1 | c2 | c3 | c4 | c5 | c6 | C7 | C8 | H1 | H2 | H3 | H4 | H5 | H6 | H7 | H8 | H9 | H10 | H11 | F1 | L1 | L2 |
| a1 | e | C6 | H11 | C8 | H5 | F1 | C1 | L2 | C3 | H6 | H7 | H4 | H3 | C4 | H1 | H2 | H9 | H8 | L1 | C2 | C5 | H10 | C7 |
| C1 | C6 | A1 | H6 | H7 | L1 | C7 | e | F1 | H2 | C2 | C3 | H8 | H9 | H10 | H11 | C8 | H4 | H3 | C4 | H1 | L2 | H5 | C5 |
| C2 | H11 | h6 | C6 | H10 | C3 | H4 | H1 | H9 | l1 | A1 | H5 | C7 | L2 | C8 | e | C4 | F1 | C5 | H2 | C1 | H3 | H7 | H8 |
| C3 | C8 | H7 | H10 | C6 | H4 | H11 | H2 | H1 | C1 | C5 | A1 | C2 | H10 | L1 | F1 | e | H5 | C4 | H8 | L2 | C2 | H9 | H6 |
| C4 | H5 | L1 | C3 | H4 | C5 | A1 | H10 | C6 | H3 | H2 | H1 | C2 | H11 | F1 | H8 | H9 | H6 | H7 | L2 | C8 | e | C7 | C1 |
| C5 | F1 | C7 | C8 | H3 | A1 | H5 | L2 | H10 | H4 | H7 | H9 | H11 | C2 | e | H2 | H8 | H1 | H6 | C1 | C3 | C4 | C6 | L1 |
| C6 | C1 | E | H1 | H2 | H10 | L2 | A1 | C5 | H7 | H11 | C8 | H9 | H8 | L1 | C2 | c3 | H3 | H4 | H5 | H6 | C7 | C4 | F1 |
| C7 | L2 | F1 | H2 | H8 | C6 | H10 | C5 | C4 | H9 | C8 | H3 | H1 | H6 | C1 | C3 | F1 | C2 | H11 | A1 | H7 | L1 | e | H5 |
| C8 | C3 | H2 | L2 | C1 | H3 | C2 | H7 | H6 | C6 | F1 | e | H10 | L1 | H4 | C5 | A1 | C4 | H5 | H9 | C7 | H11 | H8 | H1 |
| H1 | H6 | C2 | A1 | H5 | H2 | H8 | H11 | H4 | C4 | C1 | L1 | C5 | F1 | H7 | C6 | H10 | C7 | L2 | C8 | e | H9 | C3 | H3 |
| H2 | H7 | C3 | C5 | A1 | H8 | H6 | C8 | H11 | e | L2 | C1 | C4 | H5 | H9 | C7 | C6 | L1 | H10 | H3 | F1 | H1 | H4 | C2 |
| H3 | H4 | H8 | H10 | L2 | C2 | C3 | H9 | H7 | C7 | H5 | F1 | C6 | C1 | H11 | C4 | C5 | e | A1 | H1 | L1 | C8 | H6 | H2 |
| H4 | H3 | H9 | L2 | H10 | H11 | C2 | H8 | H2 | L1 | F1 | c5 | C1 | C6 | C8 | h5 | C4 | A1 | e | H6 | C7 | C3 | H7 | H1 |
| H5 | C4 | H10 | H4 | H11 | F1 | e | L1 | C1 | C2 | H8 | H6 | C3 | C8 | C5 | H9 | H1 | H7 | H2 | C7 | H3 | A1 | L2 | C6 |
| H6 | H1 | H11 | e | C4 | C5 | H9 | C2 | H3 | H5 | C6 | H10 | F1 | C5 | H2 | C1 | L1 | L2 | C7 | C3 | A1 | H8 | C8 | H4 |
| H7 | H2 | C8 | F1 | e | H9 | H1 | C3 | C2 | A1 | C7 | C6 | H5 | C4 | H8 | L2 | C1 | H10 | L1 | H4 | C5 | H6 | H3 | H11 |
| H8 | H9 | H4 | C4 | H5 | H2 | H1 | H3 | C8 | F1 | C7 | L2 | e | A1 | H7 | L1 | H10 | C1 | C6 | C2 | C5 | H2 | H11 | C3 |
| H9 | H8 | H3 | H5 | F1 | H1 | H2 | H4 | C3 | C5 | L1 | C7 | A1 | e | H6 | H10 | L2 | C6 | C1 | H11 | C4 | H7 | C2 | C8 |
| H10 | L1 | C4 | H9 | H1 | L2 | C1 | H5 | A1 | H6 | H4 | H11 | H7 | H2 | C7 | H3 | C2 | C8 | C3 | F1 | H8 | C6 | C5 | e |
| H11 | C2 | H1 | C1 | L1 | C8 | H3 | H6 | H8 | H10 | e | C4 | L2 | C7 | C3 | A1 | H5 | C5 | F1 | H7 | C6 | H4 | H2 | H9 |
| f1 | C5 | L2 | H3 | C2 | e | C4 | C7 | L1 | H11 | H9 | H8 | C8 | C3 | A1 | H7 | H6 | H2 | H1 | C6 | H4 | H5 | C1 | H10 |
| l1 | H10 | H5 | H8 | H6 | C7 | C6 | C4 | e | H1 | H3 | C2 | H2 | H7 | L2 | H4 | H11 | C3 | C8 | C5 | H9 | C1 | F1 | A1 |
| L2 | C7 | C5 | H7 | H9 | C1 | L1 | F1 | H5 | H8 | C3 | H4 | H6 | H1 | C6 | C8 | H3 | H11 | C2 | e | H2 | H10 | A1 | C4 |
Основным методом проверки правильности составления является присутствие
каждого элемента в каждой строке и в каждом столбце один раз.
Из данной таблицы находим центр группы, сравнивая строку и столбец одного и
того же элемента, т.е. определяя, коммутируют ли элементы друг с другом.
В итоге получаем следующее множество: Z (G ) = {e , a1, c 1 }.
2.4. Составление таблицы подгрупп, порожденных двумя элементами.
Подгруппы будем обозначать по тому же принципу, что и элементы, т.е. из 2-х
элементов через Ai, из 3-х элементов – Bi и т.д.
Заметим, что таблица будет симметрична относительно главной диагонали.
Используя таблицу умножений, получим:
A1={e,a1}![]() Z2
Z2
C1={e,a1,c1,c6}![]() Z4
Z4
F1={e,a1,c4,c5,f1,h5}![]() Z6
Z6
H1={e,a1,c1,c3,c6,c8,h2,h7}![]() Z8
Z8
H2={e,a1,c1,c6,h3,h4,h8,h9}![]() Z8
Z8
H3={e,a1,c1,c2,c6,h1,h6,h11}![]() Z8
Z8
L1={e,a1,c1,c4,c5,c6,c7,f1,h5,h10,l1,l2}![]() Z12
Z12
При нахождении подгрупп удобно будет пользоваться следующими
соображениями:
1. В нашем случае, согласно теореме Лагранжа, возможны подгруппы порядков 2, 4, 6, 8, 12 и тривиальные – 1, 24. Поэтому, необязательно для получения подгруппы G искать все 24 элементов, нужно найти всего 13 элементов.
2. Если на каком-то шаге мы нашли, что в нашей подгруппе имеются элементы x и y, то подгруппа тривиальная. Ведь {x,y} – это минимальная система образующих нашей группы.
| e | a1 | c1,c6 | c4,c5 | c3,c8 | C2,h11 | C7,h10 | H1,h6 | H2,h7 | H3,h4 | H8,h9 | F1,h5 | L1,l2 |
| a1 | A1 | C1 | F1 | H1 | H3 | L1 | H3 | H1 | H2 | H2 | F1 | L1 |
| c1,c6 | C1 | L1 | H1 | H3 | L1 | H3 | H1 | H2 | H2 | L1 | L1 | |
| c4,c5 | F1 | G | G | L1 | G | G | G | G | F1 | L1 | ||
| c3,c8 | H1 | G | G | G | H1 | G | G | G | G | |||
| C2,h11 | H3 | G | H3 | G | G | G | G | G | ||||
| C7,h10 | L1 | G | G | G | G | L1 | L1 | |||||
| H1,h6 | H3 | G | G | G | G | G | ||||||
| H2,h7 | H1 | G | G | G | G | |||||||
| H3,h4 | H2 | H2 | G | G | ||||||||
| H8,h9 | H2 | G | G | |||||||||
| F1,h5 | L1 | L1 | ||||||||||
| L1,l2 | L1 |
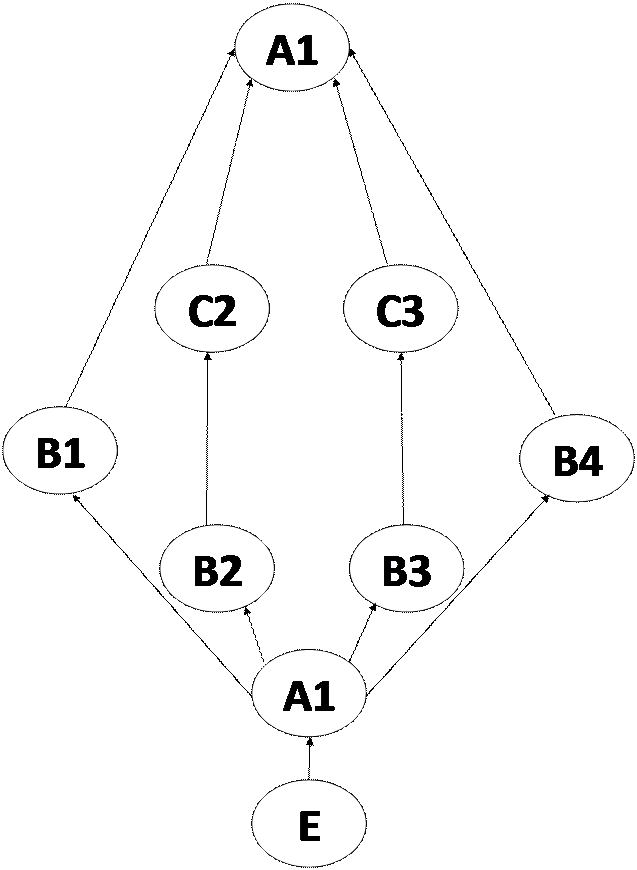
2. 5 Структура всех подгрупп.
1. А.В. Клюшин «Введение в дискретную математику» МИЭТ, 2004г.
2. А.В. Клюшин «Курс лекций по дискретной математике 2009-2010 уч. год.»
3. Кострикин А.И. «Введение в алгебру», т.1, 3.