Структура системного анализа

СОДЕРЖАНИЕ: Методология анализа сложных объектов, изучения и познания процессов. Основные принципы системного подхода к анализу проблем и основные понятия о системах. Декомпозиция, анализ подпроблем и их решение, выявление альтернатив и выбор оптимальных решений.

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

Государственное образовательное учреждение высшего профессионального образования

РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ ТОРГОВО-ЭКОНОМИЧЕСКИЙ УНИВЕРСИТЕТ

КЕМЕРОВСКИЙ ИНСТИТУТ (ФИЛИАЛ)

ФАКУЛЬТЕТ ЗАОЧНОГО ОБУЧЕНИЯ

Кафедра вычислительной техники и информационных технологий

Контрольная работа по дисциплине

“Теория систем и системный анализ”

“Структура системного анализа”

Выполнил:

студент группы ПИс-061

Жилкова Ольга Анатольевна

г. Кемерово 2007 г.

Содержание

1. Основные принципы системного подхода

2. Основные понятия о системах

3. Системный подход к анализу проблем

4. Декомпозиция

5. Анализ подпроблем

6. Решение подпроблем и выявление альтернатив

7. Выбор оптимальных решений

Литература

1. Основные принципы системного подхода

Методология анализа сложных объектов, изучения и познания процессов, протекающих в них, неразрывно связаны с теорией познания. Подход к сложному объекту, как к системе, т. е. как к совокупности взаимосвязанных и взаимодействующих его частей, формировался вместе с диалектическим пониманием процессов природы, в том числе процессов, протекающих в таком сложном объекте, как живой организм.

Основные принципы системного подхода к анализу объектов.

Поскольку под понятием система понимается совокупность взаимосвязанных и взаимодействующих подсистем, анализ следует начинать с выявлением ее структуры, т. е. состава подсистем и связей (отношений) между ними. Исследование отдельных подсистем надо вести не изолировано, а с учетом их связей. Поэтому важно суметь выделить существенные, так называемые системообразующие связи, заметно влияющие на результат исследования.

Система представляет собой не простой набор (сумму) подсистем, а целостный объект, многие свойства и возможности которого не являются простой совокупностью (суммой) возможностей ее подсистем. Из этого следует, что в ходе анализа все свойства и показатели систем должны быть разделены на целостные и аддитивные в зависимости от влияния на них эффекта взаимодействия подсистем.

Целостными называют такие свойства, функции и показатели, которые присущи только системе как целостному объекту; так, например, в химической промышленности, где синтез новых продуктов, разработку технологии и проектирование осуществляют в основном отраслевые институты, проблема развития производства и постановки новой продукции на производство должна рассматриваться как целостная подотраслевая проблема, а не проблема отдельных предприятий.

Аддитивными называют такие свойства и показатели систем, которые определяют только возможностями подсистем и представляют собой их сумму; так, например, прибыль или объем производства нормативно-чистой продукции (НЧП) отрасли равна сумме этих показателей ее предприятий и не зависит от внутренних связей системы, в отличие от выпуска товарной продукции, определяемого по заводскому методу.

При разделении свойств на целостные и аддитивные необходимо учитывать относительность многих аддитивных показателей. Так, в частности, относительность аддитивности приведенного выше показателя НЧП проявляется в том, что реализация мер по кооперированию и специализации предприятий в рамках подотрасли как системы может обеспечить повышение производительности труда и соответственно рост НЧП без увеличения численности персонала предприятий; такой рост обусловлен общесистемными (целостными) факторами.

Подсистемы взаимодействуют в процессе целенаправленного функционирования системы. Из этого следует, что при анализе систем важно выявить и тщательно изучить цель (цели) функционирования отдельных подсистем и убедиться в их соответствии целям системы. т. е. в соблюдении принципа единства цели. Если этот принцип не соблюдается, его необходимо восстановить, это существенный ресурс повышения эффективности функционирования системы.

Система связана с другими системами, т. е. с внешней средой, с помощью входных и выходных внешних связей. Из этого следует, что при анализе системы необходимо рассматривать и учитывать влияние этих связей, в том числе: учитывать воздействия внешней среды на исследуемую систему и последствия этих воздействий; оценивать функционирование системы с учетом ее воздействий на другие системы (внешнюю среду) за счет выходных связей, учитывать последствия этих воздействий.

При анализе внешних связей (так же, как это было отмечено выше, применительно к внутренним связям) важно выделить существенные.

Сложная система как объект анализа и другие системы, с которыми она связана (внешняя среда), чаще всего представляют собой развивающиеся динамические системы. Из этого следует, что при анализе систем существенную роль играет учет фактора времени. В свою очередь, фактор времени подлежит двоякому учету. Во-первых, при анализе системы и оценке ее возможностей необходимо исследовать не только статические, но и динамические свойства и характеристики. Во-вторых, особое внимание должно быть уделено исследованию ее развития и движущим силам этого развития. Такой анализ важен для познания целей и движущих сил развития, понимание закономерностей которых необходимо для обоснованного прогноза как перспектив развития системы, так и изменений ее взаимодействия с внешней средой. При исследовании движущих сил развития необходимо тщательно рассмотреть внутренние противоречия и их причинные связи.

Системный подход к исследованию сложных объектов как самостоятельное методологическое направление формировался одновременно с развитием прикладной математики и в значительной мере в результате использования количественных методов исследования. Отсюда следует, что глубина и эффективность исследования систем зависят от полноты использования этих методов для описания внешних и внутренних связей, процессов функционирования, целей системы.

Иерархическая структура сложных систем обуславливает целесообразность сочетания при их исследовании индуктивного метода (от частного – к общему) и дедуктивного (от общего – к частному).

Сопоставление сложных систем разной природы (в том числе биологических, технических и социально-экономических) показывает, что некоторые их признаки и закономерности функционирования сходны, т. е. для них в известной степени характерен изоморфизм (независимость от природы и строения системы). Поэтому при исследовании систем правомерно пользоваться методом аналогий, не доводя, разумеется, его до вульгаризации.

Таковы в общих чертах основные признаки системного подхода к исследованию объектов. Хотелось бы подчеркнуть прикладной характер и недостаточную полноту приведенного выше перечня признаков.

2. Основные понятия о системах

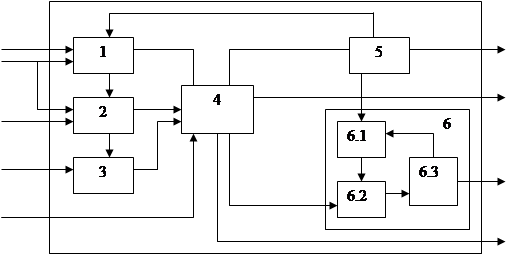
Функционирование систем. Система как совокупность взаимосвязанных и взаимодействующих подсистем может быть упрощенно представлена схемой, показанной на рисунке 1.1. Общими признаками сложных систем (биологических, технических, социально-экономических) является то, что каждая их них представляет собой структурно организованную целостную совокупность более простых частей (подсистем), взаимосвязанных и взаимодействующих в процессах целенаправленного функционирования системы.

x₁ y₁

x₂

x₃ y₂

x₄

y₃

x₅ y₄

Рисунок 1.1

1-6 – подсистемы старших рангов; 6.1-6.3 – подсистемы младших рангов

В общем случае подсистемы связаны между собой материальными, энергетическими и информационными потоками; их именуют внутренними связями. С другой стороны, каждая система связана с другими системами того же и старших рангов. Эти связи для данной системы правомерно именовать внешними. Легко убедиться, что в соответствии с принципом иерархичности внутренние связи системы будут внешними по отношению к подсистемам.

В свою очередь, все внешние связи любой системы (подсистемы) можно подразделить на входы (x1, x2, …, xi, …, …xm), которыми принято называть внешние связи (потоки), направленные к системе и реализующие внешние воздействия на систему, и выходы (y1,y2,…,yi…,yn), которыми будем называть внешние связи (потоки), исходящие от системы и представляющие собой результат ее функционирования, воздействия на другие системы, т. е. на внешнюю по отношению к данной системе среду.

Основная функция системы состоит в преобразовании (переработке) входов в выходы. Реализацию такого преобразования будем именовать процессами основной текущей деятельности системы или процессами ее функционирования в узком смысле этого понятия.

Применительно к промышленным предприятиям процессы основной текущей деятельности означают переработку ресурсов, поступающих на вход системы, в конечные результаты – продукцию и услуги. Результатами деятельности исследовательских и проектных институтов является информация, содержащаяся в выпускаемой (на выходе) научной и технической документации.

Кроме целевых (позитивных) конечных результатов, выходами системы могут быть и негативные результаты ее деятельности, например, сточные воды и выбросы в атмосферу, загрязняющие окружающую среду.

Соответственно и на входе системы наряду с ресурсами, необходимыми для ее функционирования, различают также негативные, нежелательные воздействия, нарушающие ее нормальную деятельность; их именуют возмущающими воздействиями или внешними возмущениями. Типичными примерами внешних возмущений для промышленных систем могут служить нарушения сроков поставок сырья и материалов, отклонения качества сырья от номинального, сбои в энергообеспечении и т. п.

Кроме внешних (на входе в систему), имеются и внутренние возмущения, нарушающие нормальное течение процессов функционирования, типичными примерами внутренних возмущений в производстве могут служить нарушения технологической дисциплины, аварийный выход из строя оборудования и т. д.

Важная особенность системы – целеноправленность основной деятельности проявляется в стремлении предотвратить, преодолеть или скомпенсировать возмущения, сохранить высокие целевые конечные результаты, уменьшить негативные последствия своей деятельности и экономно использовать ресурсы.

Таким образом, оценкой функционирования системы может служить ее эффективность, которая характеризуется отношением целевых конечных результатов к ресурсам, использованным как для получения этих результатов, так и для устранения (ограничения в допустимых пределах) негативных последствий функционирования.

Чтобы оценивать эффективность системы, осуществлять меры по ее поддержанию и повышению, необходимо располагать сведениями о закономерностях процессов функционирования. Целенаправленность процессов функционирования проявляется в стремлении поддерживать и повышать высокую эффективность системы, приспособляясь (адаптируясь) к изменениям внешней среды. Процессы функционирования системы (в широком смысле) – это совокупность процессов основной деятельности и разных по масштабам процессов развития и совершенствования системы.

Процессы функционирования систем нуждаются в управлении. Управление реализуется за счет целенаправленных воздействий органа управления на объект управления и обратной связи объекта с органом управления. Каждый контур управления предусматривает сбор информации о состоянии объекта (учет), ее сопоставление с заданными значениями (контроль), анализ информации и выработку управляющего воздействия (подготовку и принятие решений), а также реализацию воздействия. Совокупность органа управления системы и органов управления ее подсистем всех рангов вместе с их информационными внутренними и внешними связями составляет иерархическую систему управления.

Математическое описание процессов функционирования. Значения выходов зависят от свойств системы, от входных воздействий на нее и, как правило, от совокупности параметров внутреннего состояния системы. Кроме того, учитывая, что системы являются динамическими, входы (xi), параметры состояния системы (zi) и ее выходы (yi) изменяются во времени (t).

Математические выражения зависимостей выходов от входов и параметров состояния принято называть математическим описанием системы. Если описание достаточно правильно (адекватно) отображает фактическое поведение системы, его особенности, важные для исследования или управления, то его можно использовать для моделирования (воспроизведения) протекающих в системе процессов; в таком случае его называют математической моделью системы.

Модель системы, описывающая процессы ее функционирования в установившемся режиме, отражает статические свойства системы и называется статической моделью. График зависимости выходного показателя от соответствующего входного параметра (чаще всего основного) называют статической характеристикой. Типичными примерами статических характеристик конкретного производства могут служить зависимости объема выпуска продукции (A), себестоимости (С) и других важнейших показателей от нагрузки, т. е. от расхода (G1) основного сырья на входе в систему.

Если математическая модель описывает изменения выходов и параметров состояния системы в неустановившихся режимах (во времени), то она характеризует динамические свойства системы и называется динамической моделью. Соответственно графики изменения выходных параметров во времени при определенных воздействиях на входе принято именовать динамическими характеристиками звена (системы, подсистемы). Динамические свойства циклических процессов характеризуются также графиками, иллюстрирующими повторяемость циклов, их период, регулярность, характер колебания параметров и т. д.

Модели сравнительно простых технических систем стараются строить на основе изученных закономерностей физических и химических процессов, их функционирования; такие модели называются детерминированными.

Модели систем, которые также являются сравнительно простыми, но закономерности функционирования которых не изучены, могут быть построены в результате статической обработки результатов экспериментов. Такую систему с неизвестной структурой и свойствами иногда условно именуют “черным ящиком”, а модели, полученные указанным выше способом, в отличие от детерминированных называют статическими. При стабильности процессов, протекающих в системе, такие модели могут давать описание системы, близкое к адекватному.

Иначе обстоит дело со сложными системами. К ним относятся биологические, социально-экономические, некоторые технические системы. Для них характерно большое число подсистем многих уровней иерархии, сложность связей между ними, наличие случайных факторов, влияющих на поведение отдельных подсистем и системы в целом. В связи с этим процессы функционирования сложных систем относятся к категории так называемых случайных или стохатических процессов, а результаты функционирования не всегда предсказуемы с достаточной точностью.

Стохатические процессы характеризуются функцией распределения вероятностей рассматриваемых событий. Если эта функция стабильна, т. е. не изменяется во времени, то стохатический процесс называется строго стационарным. Для стационарных стохатических процессов функция распределения вероятностей может быть установлена экспериментально. Это позволяет, используя методы теории вероятностей, построить стохатическую модель системы; свойства таких систем характеризуются не однозначными (функциональными), а корреляционными зависимостями, позволяющими установить наиболее вероятные значения выходов и других показателей функционирования системы.

Если стохатические процессы, влияющие на поведение системы, нестационарны, то ее поведение не всегда может быть описано математически, т. е., как принято говорить, оказывается неформализуемым. Для количественной характеристики неформализуемых свойств и связей таких систем, для прогноза результатов их функционирования приходится использовать экспертные оценки специалистов и другие эвристические методы.

3. Системный подход к анализу проблем

Нередко к проблемам относят лишь очень крупные научные и хозяйственные задачи. Термин “проблема” в процессе с греческого означает задачу, задание.

Системный подход используется в ходе анализа и решения широкого круга проблем, касающихся не только управления, но и многих других областей науки и техники. В химической технологии объектом системных исследований являются главным образом структурно сложные многостадийные химико-технологические комплексы.

Каждая область применения системных исследований накладывает соответствующий отпечаток на методологию решения проблем. Существует две категории проблем: стабилизации и развития.

Проблемы стабилизации – это проблемы, решение которых направлено на предотвращение, устранение или компенсацию возмущений, нарушающих текущую деятельность системы. К решению проблем стабилизации относится также совокупность мер, которые без изменения основных характеристик системы корректируют процессы текущей деятельности; при этом учитываются изменяющиеся условия протекания установившегося производственного процесса (в том числе возникающие дополнительные возможности использования ресурсов) и колебания потребности в продукции, в том числе ее различных сортовых разновидностей.

На уровне предприятия, подотрасли и отрасли решение этих проблем обозначают термином управление производством, понимая под этим совокупность мер по управлению основным и вспомогательным производствами, материально-техническим снабжением и сбытом, а также по их текущему планированию.

Проблемами развития и совершенствования систем называются такие, решение которых направлено на повышение эффективности функционирования за счет изменения характеристик объекта управления или системы управления объектом. Решение этих проблем можно рассматривать, как совокупность мер по переводу системы из исходного состояния в новое, отличающееся от прежнего лучшими техническими характеристиками, лучшей организацией. Это обеспечивает более высокую эффективность системы.

На решение проблем развития и совершенствования промышленных систем направлено перспективное планирование производства; управление научно-исследовательскими и опытными работами, проектированием, капитальным строительством; обеспечение технического и организационного прогресса, в том числе внедрение новой техники; планирование и реализация организационно-технических мероприятий; весь комплекс работ по совершенствованию планирования и управления.

Общность проблем стабилизации процессов функционирования и проблем развития систем обусловлена единством целей, а также иногда общностью условий и средств их решения.

4. Декомпозиция

Основной операцией анализа является разделение целого на части. Задача распадается на подзадачи, система – на подсистемы, цели – на подцели и т. д. При необходимости этот процесс повторяется, что приводит к иерархическим древовидным структурам. Обычно (если задача не носит чисто учебного характера) объект анализа сложен, слабо структурирован, плохо формализован, поэтому операцию декомпозиции выполняет эксперт. Если поручить анализ одного и того же объекта разным экспертам, то полученные древовидные списки будут различаться. Качество построенных экспертами деревьев зависит как от их компетенции в данной области знаний, так и от применяемой методики декомпозиции. Декомпозиция подпроблем проводится до уровня элементарных, т. е. таких, дальнейшая конкретизация которых приводит к выявлению определенных вариантов их решения.

Обычно эксперт легко разделяет целое на части, но испытывает затруднения, если требуется доказательство полноты и безызбыточности предлагаемого набора частей. Объяснение состоит в том, что основанием всякой декомпозиции является модель рассматриваемой системы.

Операция декомпозиции представляется как сопоставление объекта анализа с некоторой моделью, как выделение в нем того, что соответствует элементам взятой модели. Поэтому на вопрос, сколько частей должно получиться в результате декомпозиции, можно дать следующий ответ: столько, сколько элементов содержит модель, взятая в качестве основания. Вопрос о полноте декомпозиции – это вопрос завершенности модели.

Итак, объект декомпозиции должен сопоставляться с каждым элементом модели-основания. Однако и сама модель-основание может с разной степенью детализации отображать исследуемый объект. Например, в системном анализе часто приходится использовать модель типа “жизненный цикл”, позволяющую декомпозировать анализируемый период времени на последовательные этапы от его возникновения до окончания. В жизни человека принято различать молодость, зрелость и старость, но можно выделять и более мелкие этапы, например детство, отрочество и юность. Такое же разнообразие может иметь место и при декомпозиции жизненного цикла любой проблемы. Разбиение на этапы дает представление о последовательности действий, начиная с обнаружения проблемы и кончая ее ликвидацией (иногда такую последовательность рассматривают как “алгоритм системного анализа”).

Установив, что декомпозиция осуществляется с помощью некоторой модели, сквозь которую мы как бы рассматриваем расчленяемое целое, далее следует ответить на естественно возникающие вопросы:

модели какой системы следует брать в качестве оснований декомпозиции;

какие именно модели надо брать.

Выше упоминалось, что основанием декомпозиции служит модель “рассматриваемой системы”, но какую именно систему следует под этим понимать? Всякий анализ проводится для чего-то, и именно эта цель анализа и определяет, какую систему следует рассматривать. Система, с которой связан объект анализа, и система, по моделям которой проводится декомпозиция, не обязательно совпадают, и хотя они имеют определенное отношение друг к другу, это отношение может быть любым: одна из них может быть подсистемой или надсистемой для другой, они могут быть и разными, но как-то связанными системами.

Например, анализируется цель “выяснить этиологию и патогенез ишемической болезни сердца”, в качестве исследуемой системы можно взять сердечно-сосудистую систему, а можно выбрать конкретный кардиологический институт. В первом случае декомпозиция будет порождать перечень подчиненных целей научного, во втором – организационного характера.

Иногда в качестве оснований декомпозиции полезно не только перебирать разные модели целевой системы, но и брать сначала модели надсистемы, затем самой системы и, наконец, подсистем. Например, при системном анализе функций Минвуза РСФСР декомпозиция глобальной цели высшего образования страны сначала проводилась по моделям вузовской системы в целом, а в конце – по моделям функционирования министерского аппарата. Можно также рассматривать и такую процедуру анализа, когда перед каждым очередным актом декомпозиции заново ставиться вопрос не только о том, по какой модели проводить декомпозицию, но и о том, не следует ли взять модель иной системы, нежели ранее.

Однако чаще всего в практике системного анализа в качестве глобального объекта декомпозиции берется нечто, относящееся к проблемосодержащей системе и к исследуемой проблеме, а в качестве оснований декомпозиции берутся модели проблеморазрещающей системы.

При всем практически необозримом многообразии моделей формальных типов моделей немного: это модели “черного ящика”, состава, структуры, конструкции (структурной схемы) – каждая в статическом или динамическом варианте. Это позволяет организовать нужный перебор типов моделей, полный или сокращенный, в зависимости от необходимости.

Однако основанием для декомпозиции может служить только конкретная, содержательная модель рассматриваемой системы. Выбор формальной модели лишь подсказывает, какого типа должна быть модель-основание; формальную модель следует наполнить содержанием, чтобы она стала основанием для декомпозиции. Это позволяет несколько прояснить вопрос о полноте анализа, который всегда возникает в явной или неявной форме.

Полнота декомпозиции обеспечивается полнотой модели-основания, а это означает, что прежде всего следует позаботиться о полноте формальной модели. Благодаря формальности, абстрактности такой модели часто удается добиться ее абсолютной полноты.

5. Анализ подпроблем

Если выявление путей достижения целей можно отнести к этапам качественного анализа проблемы, то оценка значимости каждой из подпроблем, трудоемкости ее решения, ожидаемых затрат, требуют уже количественного подхода.

Использование количественных оценок в решении организационных проблем является характерной особенностью системного анализа, важным его отличием от волевого принятия управленческих решений.

При анализе проблем управления источником количественных оценок служат в основном результаты статической обработки накопленных данных или специально собранных в ходе диагностического обследования системы, а также экспертные оценки. Нередко пользуются комбинацией двух этих источников.

Статические методы успешно используются для факторного анализа, для выявления причин отдельных нарушений и количественной оценки влияния каждого из факторов. Экспертные оценки являются основным методом ранжирования подпроблем по их значимости. Более того, экспертиза целесообразна и на стадии выявления основных недостатков функционирования системы и их причинно-следственных связей. Экспертиза широко применяется также для оценки ожидаемой трудоемкости работ, затрат на отдельные мероприятия, сроков выполнения, потребительских свойств продукции и т. д.

Весьма важным и самостоятельным направлением экспертизы является формирование различных прогнозируемых данных. Экспертные методы могут дать ориентировочные, но достаточно надежные оценки, лишь при условии методически правильной организации экспертизы.

При экспертизе относительной значимости выявленных подпроблем существенное значение имеет учет не только общей компетентности экспертов (что обычно предусматривается методикой экспертиз). Но различная степень компетентности каждого из экспертов применительно к отдельным подпроблемам. Так, например, один и тот же эксперт может дать весьма компетентную оценку действенности намеченных социологических мероприятий и в то же время не иметь достаточного опыта для правильной оценки подпроблемы, связанной с улучшением использования средств вычислительной техники.

Естественно, что при оценке затрат, трудоемкости работ и ожидаемой эффективности по каждому из направлений решения проблемы (т. е. по каждой подпроблеме) может быть сформирована самостоятельная группа экспертов, достаточно компетентная в данном частном направлении. Иначе обстоит дело, когда проводится экспертиза по определению относительной значимости совокупности подпроблем в решении общей проблемы. Именно в этих случаях и возникает необходимость учитывать разную компетентность каждого из экспертов по отношению к отдельным подпроблемам. Опыт показывает, что при таких экспертизах хорошие результаты дает использование самооценки экспертом его сравнительной компетентности в каждой из подпроблем. Следует лишь отметить, что применение самооценок компетентности требует от организаторов экспертизы проведения тщательного инструктажа экспертов, который обеспечил бы достаточно согласованный подход экспертов в выборку самооценок.

Кроме того, рассматривая вопрос об использовании экспертных методов, хотелось бы подчеркнуть, что итоги экспертизы будут более полными и результативными, если эксперты предварительно овладеют основами методологии системного анализа.

6. Решение подпроблем и выявление альтернатив

Взаимосвязь подпроблем. Отбор подпроблем, подлежащих решению, осуществляется в результате компромисса между желательной степенью достижения поставленных целей и реальными возможностями. Совокупность отобранных для решения подпроблем определяет предварительные границы проблемы, рекомендуемые на данном этапе ее анализа. Прежде чем переходить к выявлению вариантов решения элементарных подпроблем (младшего ранга), необходимо оценить значимость выявленных путей достижения целей и оставить лишь те, решение которых заметно скажется на результатах решения проблемы в целом.

При отборе подпроблем недостаточно ранжировать их по ожидаемой эффективности решения, необходимо проследить их взаимосвязи и взаимную обусловленность. Как правило, значимость подпроблем оценивают на основе экспертных оценок, максимально используя при этом результаты статических исследований объекта обследования. При экспертизе значимости подпроблем рекомендуется использовать самооценки компетентности экспертов в областях, связанных с реализацией отдельных путей достижения целей.

Таким образом, для исключения той или иной подпроблемы из программы реализации следует убедиться не только в ее относительно низкой эффективности, но и в том, что ее решение не является необходимым условием для решения одной или нескольких отобранных и намеченных для реализации подпроблем.

Взаимосвязь подпроблем определяет также последовательность их рассмотрения и решения, а следовательно – программу решения проблемы в целом. Дерево путей достижения целей дает лишь иерархическую структуру подпроблем без учета их взаимосвязей и последовательности реализации. Поэтому собственно структуризация проблемы составляет самостоятельный подэтап, выполняемый на основе анализа взаимосвязей и последовательности решения подпроблем.

Предварительное определение границ проблемы осуществляется для того, чтобы по сравнительно ограниченной совокупности отобранных подпроблем перейти к этапу сравнительного анализа и выбора вариантов их решения.

Конкретизация варианта решения по каждой из подпроблем позволяет уточнить ожидаемую эффективность его реализации и необходимые затраты, а соответственно уточнить и состав окончательной программы решения проблемы в целом. Этап завершается анализом взаимосвязи и взаимной обусловленности отдельных подпроблем. С учетом этих связей уточняется отбор подпроблем для выявления вариантов решений и определяются предварительные границы проблемы.

Выбор целевой функции и ограничений, а также структуризация проблемы позволяет переходить непосредственно к выявлению и выбору вариантов решения каждой из подпроблем и проблемы в целом. Выполнение этого этапа в значительной мере составляет предмет методологии, именуемой исследованием операций.

Рассматриваемый этап предусматривает выявление вариантов решений. Выявление вариантов – процедура практически неформализуемая, но в ходе сравнения и выбора вариантов уже в полной мере вступает в действие “математика” системного анализа. Именно здесь особенно важно творческое взаимодействие работников аппарата управления со специалистами по исследованию операции (экономической кибернетике).

В ходе этого взаимодействия организатор производства, работник аппарата управления должен активно участвовать в постановке задачи, в решении вопросов выбора исходной информации, в рассмотрении промежуточных результатов решения и уточнении постановки задачи по результатам такого рассмотрения. Наконец, работники аппарата управления полностью осуществляют экспертизу окончательного решения, его принятие и реализацию. Для выполнения этих функций важно хорошо понимать сущность задачи и возможности экономико-математических методов, но вовсе не обязательно владеть этими методами.

Основные виды решений подпроблем. Приемы выявления вариантов решений, а также методы сравнения и выбора наилучших вариантов в значительной мере определяются тремя факторами:

постановкой задачи, определяющей предмет и характер выбора;

областью использования результатов решений;

полнотой и определенностью исходной информации, используемой для выбора решений.

Основные виды решений в зависимости от перечисленных выше факторов:

Решения, зависящие от постановки задачи. По особенностям постановки задач и характеру выбора решений большинство подпроблем, по которым приходится осуществлять выбор решения в ходе управления социально-экономичнскими системами, можно разделить на три основных вида, в каждом их которых осуществляется выбор альтернативных вариантов, значений варьируемых параметров системы, состава (или структуры) формируемых комплексов.

Выбор альтернативных вариантов представляет собой сущность решения таких подпроблем, при анализе которых выявлялись два или несколько взаимоисключающих (альтернативных) варианта.

Термин “альтернатива” происходит от латинского alternare – чередование. В формальной и математической логике чаще используется термин “дизъюнкция” (от латинского disjunction – разделение), который означает, что два или несколько высказываний (положений) связаны между собой союзом “или”:

или А, или В, или С.

С использованием обозначений математической логики эта дизъюнкция может быть записана так: A v B v C.

Следует, однако, учитывать, что союз “или” может означать как неисключающие, так и взаимоисключающие разделение высказываний. Так, например, можно утверждать, что стимулирование – это поощрение или наказание. Но это утверждение не означает, что поощрение не может использоваться в сочетании с наказанием.

Вместе с тем, если рассматриваются варианты размещения проектируемого производства (на предприятии А, или В, или С), то здесь союз “или” выступает в своем взаимоисключающем значении. Такая дизъюнкция именуется строгой и означает:

или А, или В, или С, но не то и другое вместе!

Альтернативные варианты решений соответствуют именно строгой дизъюнкции, которую в математической логике принято обозначать двойным знаком: А vv B vv C.

Таким образом, задача выбора альтернатив состоит в том, чтобы из двух или нескольких взаимно исключающих вариантов решения выбрать тот единственный, который в данных конкретных условиях обеспечит наибольшую степень достижения целей.

Выбор значений варьируемых параметров системы представляет собой широкий класс так называемых оптимизационных задач по выбору режимных и конструктивных параметров отдельных аппаратов или распределению плановых заданий и ресурсов, т. е. определению значений внешних (входных и выходных) параметров производства, обеспечивающих его оптимальное взаимодействие с остальными подсистемами промышленной системы старшего ранга. К этому же классу задач относится определение обоснованных значений уровня запасов, большинства норм, нормативов и многих других параметров.

Чаще всего в подобных задачах оптимизации речь идет об одновременном определении значений совокупности варьируемых параметров, которые при заданных условиях (ограничениях) обеспечивают максимум или минимум (т. е. экстремум) соответствующей целевой функции.

Лишь в простейших задачах выбору полежит только один варьируемый параметр, но даже в этих случаях принципиальное отличие от выбора альтернативных вариантов состоит в том, что оптимальное решение является наилучшим из всех возможных в данных условиях. В то время как выбор альтернативы обеспечивает лучшее решение из числа заданных вариантов. Поэтому называть избранную альтернативу оптимальным решением неправильно, хотя такие ошибки нередко допускают, утверждая например; “из трех рассмотренных схем мы приняли оптимальную”.

Выбор состава формируемых комплексов, или набора компонентов, относится к другому классу оптимизационных задач, поскольку по своей постановке и методам решений они несколько отличаются от предыдущих.

Типичными примерами задач этого класса является выбор комплекса мероприятий, которые в пределах выделенных ограниченных ресурсов обеспечивают наибольший рост эффективности производства, выбор числа и типа, размеров оборудования. К этому же классу задач относится формирование сетевых планов выполнении комплексных работ в так называемых системах сетевого планирования и управления (СПУ). В известной мере транспортные задачи по выбору рациональных перевозок также можно отнести к рассматриваемой группе, так как в таких случаях речь идет о выборе оптимального набора последовательных отрезков пути из множества возможных вариантов или о формировании транспортной партии продуктов.

Решение, зависящие от области их использования. Методы выбора альтернатив, как будет показано ниже, мало зависят от области использования результатов решения. Вместе с тем методология решения оптимизационных задач формировалась и развивалась применительно к областям их использования. Укажем три группы таких решений: оптимальное проектирование; оптимальное управление производственными процессами; оптимальное планирование

В постановке каждой из указанных групп задач имеются особенности, заслуживающие внимания. Важной в этом смысле процедурой является выявление варьируемых параметров, оптимальные значения которых подлежат определению. Указанные выше три группы задач различаются именно по составу варьируемых параметров, выбор которых встречается в задачах проектирования и управления. А также неуправляемых факторов, влияющих на выбор решений.

Варьируемые параметры можно разделить (в первом приближении) на три основные категории:

проектно-конструктивные параметры; применительно к проектированию отдельных производств – это, как правило, размеры аппаратов, их элементов, трубопроводов, толщина слоя катализатора и т. п.; при проектировании предприятий к этой же категории варьируемых параметров можно отнести емкость складов, параметры, определяющие мощность вспомогательных производств и многие другие параметры инфраструктуры промышленной системы;

режимные параметры, которые также именутся параметрами внутреннего состояния системы; в химических производствах типичными режимными параметрами являются температура и давление в зоне реакции, концентрации компонентов;

внешние (входные и выходные) параметры системы; в промышленном производстве ими являются в основном объем выпуска продукции (А) и используемые ресурсы (G1), для предприятия же в целом – это производственная программа и ее обеспечение всеми видами ресурсов.

Неуправляемыми факторами называются такие, изменение которых в процессе функционирования системы не относится к числу управляемых воздействий. Во-первых, это неуправляемые воздействия внешней среды, в том числе внешние возмущения и изменение условий. Во-вторых, это внутренние возмущения. Применительно к задачам планирования и управления производственными системами выделим две основные категории неуправляемых факторов:

краткосрочные внешние и внутренние возмущения, в том числе изменение погодных условий, колебания качества исходного сырья, колебание параметров энергоснабжения и т. д.

изменение экономических условий (конъюнктуры), в том числе рост или снижение дефицитности ресурсов, потребности в продукции и др.

С учетом принятой классификации варьируемых параметров и неуправляемых факторов особенности задач оптимального проектирования, управления и планирования состоят в следующем:

При оптимальном проектировании экономические условия и плановые показатели бывают заданы, а возмущения не учитываются; для неуправляемых факторов принимаются вероятные или номинальные значения. Выбору подлежат оптимальные значения проекто-конструктивных и режимных параметров.

При оптимальном управлении процессами производство уже реализовано, т. е. конструктивные параметры известны и не изменяются, а плановые задания и экономические условия заданы, а возмущения не учитываются; для неуправляемых факторов принимаются вероятные или номинальные значения. Выбору подлежат оптимальные значения проектно-конструктивных и режимных параметров.

При оптимальном планировании известны конструктивные параметры; показатели производства принимаются, исходя из условия их поддержания системой управления на оптимальном уровне при вероятных значениях неуправляемых параметров (текущее планирование на год) или при их фактических значениях (оперативное планирование). Выбору подлежат плановые задания, которые обеспечивают экстремум целевой функции в изменившихся экономических условиях.

С наиболее сложной категорией оптимизационных задач мы сталкиваемся при перспективном планировании. В них сочетаются стремления к оптимальному использованию действующих мощностей (близкое к рассмотренной выше задаче текущего планирования) и к развитию промышленной системы. Выбор решений по развитию производственных мощностей и инфраструктуры должен обеспечить максимальный прирост целевой функции системы в пределах выделенных ресурсов. Изменение экономических условий (конъюнктуры) в плановом периоде подлежит прогнозированию.

Принятие решения на основе исходной информации различной полноты. Чтобы использовать математические (формализованные) методы выбора решений, необходимо располагать полной и достаточно определенной информацией.

Полноту информации, используемой для выбора альтернативных вариантов, будем считать такую, которая позволяет определить численные значения целевой функции для каждой из сравниваемых альтернатив в условиях заданных ограничений.

Для решения оптимизационной задачи необходимо также располагать заданными ограничениями и иметь возможность построить целевую функцию, которая зависела бы только от варьируемых (искомых) параметров и известных (заданных) показателей. Иногда утверждают, что для этого необходимо знать зависимости всех выходных параметров системы от всех ее входных параметров. Такое утверждение не вполне обосновано. Требования к полноте математического описания процесса функционирования системы зависят от конкретной постановки задачи; ниже это будет показано на примерах.

Определенной будем именовать информацию об однозначно предсказуемых значениях параметров и условиях. Такую информацию мы имеем лишь при строго формализованной целевой функции и при описании свойств объекта исследования детерминированными либо статическими моделями.

Сложные системы находятся под воздействием случайных факторов. При строго стационарных стохатических процессах для выбора решения используется вероятностный подход. Это означает, что принимаемое решение обусловливает определенный риск и с некоторой вероятностью является наилучшим.

Наконец, при нестационарных случайных воздействиях значения параметров процесса и условий чаще всего математически непредсказуемы.

Таким образом, по полноте и определенности исходной информации можно выделить три методологических подхода, позволяющих выбрать решение однозначно, с определенной степенью вероятности и в условиях неопределенности.

Строгий выбор решения, однозначно определяющего результат, может быть получен формализованными методами исследования операций при наличии полной и определенной исходной информации.

Выбор решения, определяющего результат с определенной вероятностью и оценивающего степень риска, может быть получен формализованными методами с использованием теории вероятностей, если система описывается стохатическими моделями, а объем информации достаточно полный.

Решение принимается в условиях неопределенности, когда отсутствует необходимая информация, либо потому, что не было проведено должное исследование системы, тенденции ее развития и внешних условий, либо потому, что система находится под воздействием нестационарных случайных факторов. Особый случай принятия решений в условиях неопределенности – это выбор стратегии в ходе состязательной борьбы. Для принятия решений в условиях неопределенности используются эвристические методы, теория игр и комбинированные методы, в том числе имитационное моделирование.

Человеко-машинное исследование развития ситуации (ее имитация, “проигрывание”) представляет собой имитационное моделирование. Оно основано на том, что процесс функционирования системы или перспективы ее развития могут быть частично описаны формализовано, а некоторые условия (элементы решение, коэффициенты целевой функции и другие данные) должны приниматься эвристичеки. В этих случаях суть имитационного моделирования состоит в том, что часть данных принимается эвристичеки, а часть (развитие ситуации на некотором этапе для принятых условий) рассчитывается на ЭВМ с использованием зависимостей, которые поддаются формализации.

Выявление альтернатив - это нахождение двух или нескольких взаимно исключающих вариантов решения. Примерами крупных, принципиальных альтернатив могут служить направления технической политики, стратегия развития промышленной системы и т. д. Примерами более частных альтернатив, выявлять и решать которые приходится повседневно, являются решение о том, стоит ли осуществлять то или иное мероприятие, выбор одного из возможных вариантов мероприятий, выбор лиц на замещение определенной должности и т. д.

Нередко возможные альтернативные варианты выдвигает сама обстановка, конкретные условия. Тогда необходимость в подобной самостоятельной процедуре отпадает. В то же время, если подпроблема может иметь разные, но еще не ясные варианты решения, то выявление этих вариантов представляет собой ответственную и сложную процедуру. Опыт показывает, что наиболее полно удается выявить альтернативы, привлекая для этого группу специалистов (экспертов). Причем на первом этапе целесообразно провести анкетирование, чтобы каждый эксперт дал свои варианты в независимо от других. А затем провести дискуссию в сравнительно узком кругу и в условиях, которые именуются иногда “мозговым штурмом”. В наиболее ответственных случаях предварительный перечень альтернатив, подготовленный указанным выше способом, можно представить на рассмотрение более широкой аудитории.

При выявлении альтернатив следует помнить, что зачастую сравниваемые варианты только на первый взгляд кажутся взаимоисключающими. При более тщательном анализе удается выявить возможность некоторой их комбинации или найти промежуточный вариант, который в значительной степени сохраняет положительные качества исходных сравниваемых вариантов, но в то же время не имеет многих присущих им негативных особенностей. В этом суть диалектического подхода к выбору решения. В самом деле, из определения существа альтернатив следует, что они взаимно исключают, т. е. взаимно отрицают одна другую. Поэтому поиск нового промежуточного варианта как комбинации исходных есть отрицание отрицания:

Выбор альтернатив в условиях определенности, как правило, не представляет особых затруднений. Пользуясь принятыми выше понятиями полноты и определенности информации, будем руководствоваться следующим выводом: при наличии достаточной исходной информации выбор варианта осуществляется на основании сопоставления значений целевой функции по всем сравниваемым варианта, с учетом заданных ограничений.

Выбор альтернатив в условиях неопределенности. Принято считать, что альтернативные решения выбираются в условиях неопределенности, если исходной информации недостаточно для определения численных значений целевой функции по каждому из сравниваемых вариантов. Подход к выбору решений в таких случаях требует, в первую очередь, анализа характера неопределенности, уточнения того, какой именно информации недостает и по каким причинам.

В теории исследования операций выделяют три основные категории неопределенности, когда исходная информация не позволяет однозначно определить соответственно:

цели;

условия и последствия решения проблемы;

действия противоборствующей стороны в состязательных задачах.

Рассмотрим кратко эти категории.

Неопределенность целей. Когда не удается воспользоваться строго расчетными оценками, соизмерение подцелей осуществляется на основании экспертизы, что вносит некоторую неопределенность.

Нередко возникают трудности в оценке экономических последствий дефицитности продукции и различных видов ресурсов, в оценке эффективности решения социальных задач, влияние сроков выполнения работ и других факторов.

Неопределенность условий и последствий решения проблемы при социалистическом способе производства возникает, главным образом, вследствие случайных внутренних и внешних возмущений, колебаний погодных условий, неизвестности времени наступления и силы стихийных бедствий. Изменений внешнеполитической обстановки, открытий новых запасов полезных ископаемых, колебаний спроса, обусловленных изменениями предпочтений людей и отдельных социальных групп. В том числе изменения моды, и т. д.

Следует также отметить специфическую неопределенность, обусловленную высокими темпами научно-технического прогресса. Так, время появления открытий, изобретений не является в полной мере предсказуемыми. Вместе с тем они оказывают существенное влияние на развитие социально-экономических систем. Именно этот вид неопределенностей рассматривается как характерный при выборе альтернативных вариантов планирования исследовательских и опытных работ. С одной стороны, желательно сократить сроки разработки, но при этом трудно ожидать высокоэффективных, конкурентоспособных решений. С другой стороны, можно сосредоточить на исследованиях значительные ресурсы и увеличить плановые сроки работ, но при этом увеличиться риск, что за достаточно длительное время появятся новые зарубежные патенты, которые нарушат патентную чистоту прогнозируемых результатов исследования.

Тот же научно-технический прогресс обусловливает и неопределенность другого вида: сравнительно быструю смену способов производства многих продуктов и смену ассортимента. В результате не вполне предсказуемыми оказывается изменения потребности в отдельных видах конечной продукции и сырья.

Таковы в основном характерные для химической индустрии неопределенности рассматриваемой категории.

Неопределенность действия противоборствующей стороны. В работах западных специалистов по исследованию операций и системному анализу значительное внимание уделяется именно этой категории неопределенностей и выбору решений (стратегий) на основе использования методов теории игр. Это внимание обусловлено тем, что основным объектом системного анализа в капиталистических странах и экономические исследования происходят в условиях острой конкурентоспособной борьбы.

В социалистическом обществе для промышленных систем подобные задачи актуальны лишь в области внешней торговли на мировом рынке, а потому не характерны при исследованиях внутриотраслевых проблем.

7. Выбор оптимальных решений

Постановка и решение задач оптимизации.

Как правило, этап выбора оптимальных решений состоит из двух основных процедур:

постановки оптимизационной задачи;

собственно решения задачи, т. е. отыскания значений варьируемых параметров или состава формируемого комплекса, которые обеспечивают максимальную степень достижения цели в заданных конкретных условиях.

При постановке задачи для решения оптимизационной задачи необходимо построить:

целевую функцию или критерий оптимальности, которые зависели бы только от варьируемых (искомых) параметров и известных (заданных или измеряемых) показателей;

систему ограничений, определяющих заданные условия решения задачи и содержащих также лишь искомые и известные величины.

Эту процедуру построения целевой функции и системы ограничений принято именовать постановкой (или математической постановкой) оптимизационной задачи.

Но не следует полагать, что выбрав, например, показатель народнохозяйственного дохода в качестве целевой функции, завершается основная часть математической постановки задачи. По своему экономическому содержанию выбор целей функции или критерия оптимальности является важным этапом, но он скорее предшествует математической постановке задачи, а не входит в нее в качестве составляющего.

Приступая к разработке содержательной и математической постановки оптимизационной задачи, в первую очередь необходимо дать четкую формулировку сущности задачи.

Следующая процедура – это уточнение объекта оптимизации. Уточняя объект оптимизации, следует подчеркнуть, что речь идет не о проектируемом, а о действующем производстве. Когда уже не рассматривается соизмерение регулярных и единовременных затрат. Закончено не только строительство, но и реконструкция (в нашем случае – замена катализатора), а следовательно, единовременные затраты по данному производству (Кв) должны рассматриваться, как неименные.

Дальнейшей процедурой постановки оптимизационной задачи следует считать выбор варьируемых переменных. По определению, варьируемыми переменным следует считать те параметры, выбор значений которых зависит от нас и должен обеспечить максимальную степень достижения целей. Это искомые значения параметров.

В общем случае при выполнении этой процедуры необходимо:

выделить все те параметры, изменение которых зависит от нас, а определение оптимальных значений составляет суть задачи.

рассмотреть позитивные и негативные последствия изменений этих параметров на функционирование объекта и убедиться (пока качественно), что в пределах допустимых изменений этих параметров может существовать наивыгоднейший компромисс между выигрышем в достижении одних подцелей и проигрышем в достижении других;

рассмотреть взаимосвязи выделенных параметров и выбрать взаимно независимые, учитывая при прочих равных условиях, какие из взаимосвязанных параметров наиболее употребительны (являются основными) в принятой системе техническо-экономических показателей производства.

Следующая процедура постановки задачи состоит в том, чтобы выразить целевую функцию (критерий оптимальности) через варьируемые параметры и заданные (известные) величины.

Математическое описание должно позволять исключить неварьируемые переменные и из системы ограничений. Построение системы ограничений проводится параллельно с формированием целевой функции на основании заданных условий решения задачи.

Решение задачи и анализ результатов. Нахождение численных значений варьируемых переменных, соответствующих условиям, заложенным в постановке задачи, составляет процедуру, именуемую собственно решением задачи. Для решения оптимизационных задач используются разнообразные методы математического программирования, выбор которых зависит от особенностей постановки задачи и от ее размерности. Под размерностью понимается общее число варьируемых переменных и использованных ограничений.

Как правило, решение сравнительно сложных оптимизационных задач осуществляется на ЭВМ. Лишь в простейших случаях решение может быть получено с помощью обычных методов определения экстремумы функции при несложных расчетах, а также табличными или графическими способами.

Получив решение оптимизационной задачи, следует подвергнуть его анализу. Последний вариант проверки позволит также оценить чувствительность оптимума, т. е. установить, существенной ли будет потеря эффективности при некоторых отклонениях от найденного оптимума.

Основной принцип системного подхода состоит именно в том, что решение любой проблемы для отдельной подсистемы должно осуществляться с учетом ее взаимодействия с остальными подсистемами, исходя из интересов системы в целом. Решение многих оптимизационных задач позволяет получить не только искомые значения варьируемых параметров, но и частичные производственные целевой функции по ограничениям, характеризующим предельные значения прироста эффективности (или ущерба) на единицу соответствующего ресурса – так называемые двойственные оценки.

Литература

1. Губанов В.А., Захаров В.В., Коваленко А.Н., Введение в системный анализ: Учеб. пособие / Под ред. Л.А. Петросяна. – Л.: Издательство Ленинградского университета. 1988. 232 с.

2. Диалектика и системный анализ, под ред. Д.М. Гвишиани. – М.: - “Наука”, 1986. – 336 с.

3. Добкин В.М., Системный анализ в управлении – М,: Химия, 1984. – 224 с., ил.

Скачать архив с текстом документа