Структурный синтез активных фильтров ВЧ и СВЧ диапазонов
СОДЕРЖАНИЕ: Анализ свойств R-фильтров второго порядка. Особенность схемотехники звеньев R-фильтров нижних частот. Характеристика синтеза структур R-звеньев с дополнительными частотнозависимыми цепями. Синтез фильтра третьего порядка с дополнительными RC-цепями.Содержание
1. Предварительные замечания
2. Основные свойства R-фильтров второго порядка
3. Особенность схемотехники звеньев R-фильтров нижних частот
4. Синтез структур R-звеньев с дополнительными частотнозависимыми цепями
5. Синтез ФНЧ третьего порядка с дополнительными RC-цепями
Библиографический список
1. Предварительные замечания
Внедрение SiGe технологии в широкую инженерную практику открывает объективные возможности построения твердотельных элементов и устройств диапазона высоких и сверхвысоких частот. Причем это относится не только к простейшим узлам, но и к более сложным устройствам, где реализация нужных функциональных свойств и совокупности количественных показателей обеспечивается применением специальных цепей обратной связи с глубоким возвратным отношением.
Важным дополнительным технологическим ограничением, существенно влияющим на схемотехнику таких устройств, является минимизация числа контактных площадок, потребляемой мощности при сохранении импедансных соотношений. Кроме этого, можно также с уверенностью утверждать, что изменяется не только структура, но и схемотехника базовых активных элементов, необходимых для построения более сложных функциональных устройств. Именно поэтому, за исключением диапазона рабочих частот, потенциально достижимые иные качественные показатели усилителей, преобразователей напряжения – ток (ПНТ) и ток – напряжение (ПТН) окажутся более низкими. Применительно к устройствам частотной селекции – активным фильтрам, амплитудным и фазовым корректорам – такой вывод существенно влияет на возможный набор альтернативных способов их схемотехнической реализации. Например, при создании высокоселективных (высокодобротных) фильтров или корректоров невозможно использовать гираторы на ПНТ, а ориентация на RLC-базис в частотозадающих цепях из-за индуктивности приводит к недопустимому увеличению площади кристалла.
Сомнительно также и применение структур с решающими усилителями. Несмотря на относительно низкое влияние частоты единичного усиления усилителей на основные параметры конечных устройств низкое значение частотозадающих резисторов (102 Ом) приводит к необходимости развивать в выходных каскадах большие (101 мА) токи.
Для уменьшения поэлементной чувствительности, позволяющей повысить точность реализации частотных характеристик, в структуре фильтров высокого порядка обычно используются дополнительные межзвенные связи [3]. Однако в области относительно высоких частот, когда отношение центральной частоты (частоты настройки) к относительной ширине полосы пропускания соизмеримо с частотой единичного усиления, использование таких обратных связей оказывается невозможным. Именно поэтому основным способом построения активных фильтров и корректоров является каскадирование секций (звеньев) второго и первого порядков.
Собственная компенсация влияния частоты единичного усиления существенно уменьшает соответствующую чувствительность параметров звеньев второго порядка и поэтому расширяет диапазон рабочих частот фильтра. Этот путь построения селективных устройств и СФ блоков представляется естественным при условии, что компенсирующие обратные связи не приводят к заметному уменьшению запаса устойчивости по фазе, необходимому для устойчивой работы схемы.
Именно поэтому при разработке соответствующих ОУ необходимо учитывать «электрическую длину» как по основным, так и по дополнительным контурам обратной связи [9]. Например, принципиальная схема звена полосового типа практически точно удовлетворяет этому критерию, поэтому при практической ее реализации необходим дифференциальный ОУ с относительно невысокой скоростью нарастания выходного напряжения.
Максимальное выходное напряжение фильтра будет определяться только этим параметром, т.к. эффект «перенапряжений» в схеме звена отсутствует. Кроме этого , уровень синфазного напряжения ОУ2 достаточно мал и определяется отношением максимального выходного напряжения фильтра к дифференциальному коэффициенту усиления ОУ.
Поэтому при разработке ОУ можно руководствоваться неравенствами
![]() ;
; ![]() ;
; ![]() , (1)
, (1)
которые справедливы при полной компенсации влияния П1 =2f1 как на частоту, так и на затухание полюса.
Для построения звена полосового фильтра для систем связи при условии реализации соответствующих СФ блоков в технологическом процессе SGB25VD с параметрами, указанными в табл. 1, был разработан ОУ с дополнительными (не указанными в табл. 1) параметрами =330 ; I0 =10 мА; Еп =±2,0 В; Rн min = 50 Ом.
Учитывая невысокую нагрузочную способность ОУ и низкое значение статического коэффициента усиления, при расчете звена необходимо учитывать влияние этих параметров:
![]() ;
; ![]() ;
; 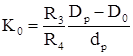 .
(2)
.
(2)
Поэтому при моделировании схемы фильтра в среде Cadence использовались следующие номиналы пассивных элементов:
С1=С2=0,2 пФ; R1=3,2 кОм; R2=50 Ом; R3=100 Ом; R4=650 Ом; R5=.
Таблица 1 Результаты проектирования звена для технологического процесса SGB 25 VD |
||||||||
Базовые параметры |
Основные параметры фильтра | Основные параметры ОУ | ||||||
| fp , (Гц) | Q | K0 | Uвых max , (мВ) | f1 , (ГГц) | v, (В/мкс) | Ксн , (Дб) | ||
| Расчет | 1,7 | 2,2 | 2 | 250 | - | - | - | - |
| Моделирование | 1,69 | 2 | 1,95 | 230 | 8,4 | 56 | 3000 | -55 |
| Погрешность, (%) | 0,6 | 10 | 2,5 | 8,7 | - | - | - | - |
Приведенные в табл. 1 результаты демонстрируют хорошую сходимость экспериментальных и расчетных значений. Дополнительно отметим, что в настоящем фильтре второго порядка Qfp =3,4 ГГц, что только в 2,5 раза меньше частоты единичного усиления ОУ. Именно этот интегральный показатель и характеризует качество схемотехнического решения задачи [5, 12].
Полученные результаты позволяют сделать достаточно важные для схемотехники СФ блоков с узлами частотной селекции выводы.
Во-первых, структуры с собственной и взаимной компенсацией уменьшают требования к активным элементам и создают дополнительные степени свободы при схемотехническом проектировании СВЧ ОУ.
Во-вторых, собственная компенсация позволяет повысить общую стабильность характеристик устройства частотной селекции. Напримерчувствительность основных параметров фильтра к нестабильности всех компонентов схемы не превышает 0,5, а при С1 =С2 чувствительность добротности к этим параметрам нулевая, что можно использовать, в частности, и для функциональной настройки звена на заданную частоту полюса.
Наконец, и это самое главное, работоспособность в ВЧ и СВЧ диапазонах схем с собственной и взаимной компенсацией является важным аргументом для широкого внедрения в соответствующих СФ блоках узлов и устройств с комплексом обратных связей, направленных на обеспечение необходимых функциональных зависимостей как СФ блоков, так и СнК в целом. Однако дальнейшее расширение диапазона рабочих частот требует пересмотра подхода к схемотехническому проектированию этого класса устройств.
2. Основные свойства R-фильтров второго порядка
При использовании в качестве частотозадающих цепей ограниченность полосы пропускания операционных усилителей в звеньях второго порядка необходимо применить только два активных элемента (n=2). В этом случае
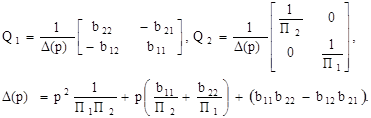 (3)
(3)
![]() являются передачами пассивной подсхемы с учетом влияния входного и выходного сопротивлений ОУ с выхода i-го ОУ на инвертирующий (индекс «-») и неинвертирующий (индекс «+») входы j-го ОУ. Можно строго показать, что в классе рассматриваемых схем реализация как заграждающих фильтров, так и фильтров верхних частот невозможна. Указанный вывод, который следует из постановки задачи, справедлив при условии аппроксимации ОУ передаточной функцией 1-го порядка. Если ОУ и любой усилитель с конечным
являются передачами пассивной подсхемы с учетом влияния входного и выходного сопротивлений ОУ с выхода i-го ОУ на инвертирующий (индекс «-») и неинвертирующий (индекс «+») входы j-го ОУ. Можно строго показать, что в классе рассматриваемых схем реализация как заграждающих фильтров, так и фильтров верхних частот невозможна. Указанный вывод, который следует из постановки задачи, справедлив при условии аппроксимации ОУ передаточной функцией 1-го порядка. Если ОУ и любой усилитель с конечным ![]() характеризуется функцией 2-го порядка, то реализация вполне реальна.
характеризуется функцией 2-го порядка, то реализация вполне реальна.
С учетом структуры матрицы Q1 можно утверждать, что для реализации передаточной функции звена полосового типа необходимо выполнить одно из условий b22 =0 или b11 =0. Несложно также установить, что указанные варианты отличаются только номерами ОУ (изоморфные решения). Именно поэтому без потери общности выводов можно положить, что
![]() . (4)
. (4)
В этом случае после приведения передаточной функции звена к стандартной форме получим
 , (5)
, (5)
где
![]() ,
, 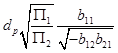 , (6)
, (6)
 . (7)
. (7)
Таким образом, на выходе первого ОУ реализуется передаточная функция звена полосового типа, а на выходе второго ОУ – функция звена фильтра нижних частот. Отметим, что знак bij , как было показано ранее, легко изменяется путем выбора инвертирующего и неинвертирующего входов любого из ОУ. Как следует из (6), выбор частоты полюса при конкретном типе ОУ может осуществляться за счет коэффициента сдвига
![]()
![]() . (8)
. (8)
Следовательно, для реализации высокой добротности ![]() необходима (7) низкая глубина местной отрицательной обратной связи в первом ОУ
необходима (7) низкая глубина местной отрицательной обратной связи в первом ОУ ![]() . Из соотношений и можно определить набор локальных передаточных функций для каждого из возможных фильтров. Для полосового фильтра
. Из соотношений и можно определить набор локальных передаточных функций для каждого из возможных фильтров. Для полосового фильтра
 , (9)
, (9)
 , (10)
, (10)
и для фильтра нижних частот
 , (11)
, (11)
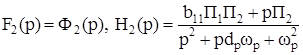 . (12)
. (12)
Максимальное значение модулей этих функций непосредственно характеризует динамический диапазон устройства. Так, для полосового фильтра и фильтра нижних частот
 (13)
(13)
 . (14)
. (14)
Таким образом, выбором численных значений коэффициентов передачи цепей связи первого и второго ОУ (![]() ) можно обеспечить при любых частотах их единичного усиления и любом коэффициенте сдвига (8) максимально эффективное использование линейного участка амплитудной характеристики активных элементов. Для оценки влияния ОУ на собственный шум фильтров можно из соотношения выделить максимальное значение выходной спектральной плотности при условии равномерности в диапазоне рабочих частот (в окрестности частоты полюса wP
) входной спектральной плотности активных элементов
) можно обеспечить при любых частотах их единичного усиления и любом коэффициенте сдвига (8) максимально эффективное использование линейного участка амплитудной характеристики активных элементов. Для оценки влияния ОУ на собственный шум фильтров можно из соотношения выделить максимальное значение выходной спектральной плотности при условии равномерности в диапазоне рабочих частот (в окрестности частоты полюса wP
) входной спектральной плотности активных элементов
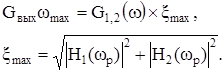 (15)
(15)
В этом случае, как это видно из (9)–(12) для полосового фильтра,
![]() (16)
(16)
а для фильтра низких частот
![]() (17)
(17)
Для сравнения отметим, что при ![]() в ARC-фильтрах аналогичная оценка приводит к следующему результату
в ARC-фильтрах аналогичная оценка приводит к следующему результату
![]() . (18)
. (18)
Как видно из приведенных соотношений, «проигрыш» R фильтров непосредственно определяется численным значением коэффициента сдвига bz , который также влияет и на максимальное выходное напряжение (Umax ) ОУ в рабочем диапазоне частот. Действительно, в области относительно высоких частот (соизмеримых с частотой единичного усиления) Umax определяется не через амплитудную характеристику ОУ (U0 ), а зависит от скорости нарастания выходного напряжения U ОУ. Из [5] следует, что
![]()
![]() , (19)
, (19)
где Uri – граничное напряжение входного каскада Qi-го ОУ.
Таким образом, при идентичных ОУ минимизация верхнего уровня динамического диапазона связана с реализацией условия
![]() (20)
(20)
и применением в структуре входных каскадов ОУ нелинейных цепей коррекции, направленных на увеличение Ur . Из соотношений (14), (16), (17), (19) следует, что
 (21)
(21)
где D – диапазон рабочих частот фильтра.
При использовании традиционных схемотехнических решений ОУ для SiGe технологии можно считать, что
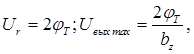 (22)
(22)
поэтому
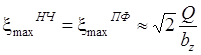 . (23)
. (23)
Приведенные оценки и определяют в основном область компромисса при проектировании R-фильтров.
3. Особенность схемотехники звеньев R -фильтров нижних частот
Для звеньев второго порядка ФНЧ условие (4) можно исключить, тогда, как следует из (3), основные параметры будут иметь следующий вид
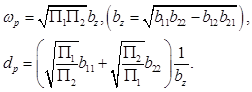 (24)
(24)
Перебор вариантов реализации ![]() показывает, что
показывает, что ![]() , поэтому параметры передаточной функции (5) можно конкретизировать:
, поэтому параметры передаточной функции (5) можно конкретизировать:
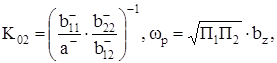
![]() ,
,
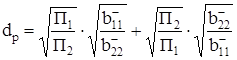 .(25)
.(25)
Таким образом, сдвиг частоты полюса в область более низких частот ![]() сопровождается увеличением коэффициента усиления звена K02
. Однако в любом случае минимальное значение затухания полюса соответствует аналогичному параметру разделенной пассивной RC-цепи
сопровождается увеличением коэффициента усиления звена K02
. Однако в любом случае минимальное значение затухания полюса соответствует аналогичному параметру разделенной пассивной RC-цепи ![]() , что препятствует реализации ФНЧ со специальными свойствами (например, ФНЧ с линейной ФЧХ). Тогда при П1
=П2
,
, что препятствует реализации ФНЧ со специальными свойствами (например, ФНЧ с линейной ФЧХ). Тогда при П1
=П2
, ![]() в диапазоне рабочих частот
в диапазоне рабочих частот
![]() (26)
(26)
![]() . (27)
. (27)
Таким образом, эффекта «перенапряжения» не наблюдается и верхняя граница динамического диапазона определяется соотношением (19), а собственный шум схемы – коэффициентом влияния (15)
 (28)
(28)
и, следовательно, при большем К02 первым ОУ. Однако при небольших коэффициентах передачи «вклад» ОУ в собственный шум схемы практически одинаков.
Полученные соотношения показывают, что основной задачей этапа схемотехнического проектирования безъемкостных ФНЧ является создание структур, в рамках которых параметрическая оптимизация обеспечивает реализацию любых значений добротности при более низком влиянии ОУ на собственный шум звена второго порядка. Как было показано ранее, решение такой задачи возможно применением принципа собственной компенсации влияния, по крайней мере, одного из ОУ. Для уменьшения затухания полюса, вызванного влиянием площади усиления доминирующего ОУ, на его выходе должна быть реализована передаточная функция ФНЧ, а возвратное отношение дополнительной (компенсирующей) обратной связи должно быть положительно.
Принципиальная схема приведена на рис. 1.

Рис. 1. Звено R-фильтра с собственной компенсацией влияния ОУ2
Для наглядности и упрощения последующих соотношений будем использовать базовые параметры масштабных усилителей
 (29)
(29)
В базисе указанных аргументов параметры передаточной функции Ф2(р ) будут определять следующими соотношениями
 (30)
(30)
при выполнении параметрического условия собственной компенсации
![]()
![]() , при
, при ![]() ,
,
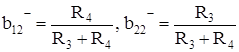 , (31)
, (31)
![]() , где
, где ![]() ,
, ![]() .
.
Аналогично при тех же условиях определяются локальные передаточные функции
 (32)
(32)
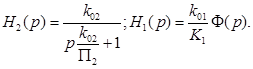 (33)
(33)
Таким образом, как это следует из (19) и (20), максимальное выходное напряжение звена определится следующим выражением
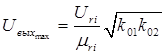 (34)
(34)
при условии
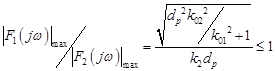 . (35)
. (35)
Соотношение (35) является оценочным при ![]() .
.
При аналогичном допущении определяется коэффициент влияния ОУ1 и ОУ2 на собственный шум схемы
![]() . (36)
. (36)
Таким образом, введение компенсирующего контура обратной связи существенно уменьшило влияние ОУ2 на основные качественные показатели схемы звена второго порядка. Для построения и моделирования принципиальных схем разработан, ориентированный на SiGeтехнологию, SGB25VD (IHP) ОУ, базовые параметры которого показаны в табл. 2. Здесь и далее приводятся результаты моделирования принципиальных схем в среде Cadence.
Таблица 2
Основные параметры ОУ для технологии SGB 25 VD
(дБ) |
(Ггц) |
(В/мкс) |
(В/мкс) |
(мВ) |
(Ом) |
(В) |
(мА) |
| 38 | 2 | 900 | 425 | 400 | 50 | 5,5 |
Предварительно отметим, что возможность работать этого ОУ на низкоомную нагрузку и, следовательно, стандартную СВЧ линию позволяет совместить функцию фильтра и драйверного усилителя с заданным коэффициентом передачи. На рис. 2 приведены АЧХ и ФЧХ такого R-фильтра с коэффициентом передачи ![]() =30 дБ и добротностью
=30 дБ и добротностью ![]() (кривые 1 и 2 соответственно). Здесь же для демонстрации эффективности действия контура компенсирующей обратной связи приведены аналогичные характеристики при
(кривые 1 и 2 соответственно). Здесь же для демонстрации эффективности действия контура компенсирующей обратной связи приведены аналогичные характеристики при ![]() , когда
, когда ![]() (кривые 3 и 4).
(кривые 3 и 4).
Совпадение частоты полюса звена при различных добротностях показывает также недоминирующее влияние вторых полюсов используемых ОУ на параметры ФНЧ. Эффективность использования частотных свойств ОУ видна также из сопоставления АЧХ R-фильтра и АЧХ масштабных усилителей (кривая 5). Анализ временных характеристик ФНЧ (Q=1) при гармоническом входном воздействии различных уровней(рис. 3) показывает, что длительность переходного процесса согласуется с линейной моделью фильтра, а максимальное выходное напряжение (вторая гармоника соответствует максимальному коэффициенту передачи фильтра) не менее 100 мВ.
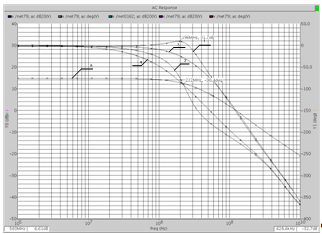
Рис. 2. Частотные характеристики R-ФНЧ
при разных добротностях полюса и k02 =30 дБ
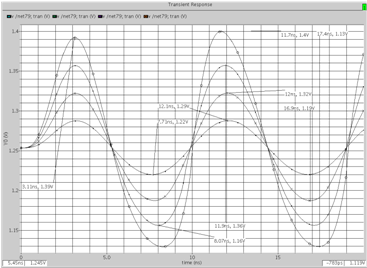
Рис. 3. К определению максимального выходного напряжения
R-ФНЧ с Q=1
Как видно из соотношений (25), увеличение частоты полюса ФНЧ связано с уменьшением его коэффициента передачи в полосе пропускания. Результаты моделирования и сопоставительного исследования схемы (рис. 1) на базе экспериментального ОУ (табл. 1) приведены в табл. 3.
Таблица 3
Результаты моделирования звена R -фильтра
с собственной компенсацией
(дБ) |
(%) |
(МГц) |
(%) |
(%) |
(мВ) |
||
| 30 | 1,5 | 222 | 25 | 1,22 | 7,4 | 100 | 36 |
| 0 | 0 | 642 | 29,4 | 1,19 | 5 | 100 | 36 |
| Примечание. |
|||||||
Более детальное изучение приведенной в табл. 3 погрешности реакции основных параметров ФНЧ позволяет предположить, что указанное отклонение частоты полюса (![]()
![]() ), коэффициентов передачи (
), коэффициентов передачи (![]()
![]() ) и (
) и (![]()
![]() ) обусловлено эффектом умноженияпаразитной входной емкости дифференциальных каскадов ОУ, а также влиянием второго полюса его ФНЧ.
) обусловлено эффектом умноженияпаразитной входной емкости дифференциальных каскадов ОУ, а также влиянием второго полюса его ФНЧ.
Однако область применения полученного устройства ограничивается уровнем его динамического диапазона, когда, как видно из (32) и (27), необходимость увеличения k02
, k2
приводит к практически пропорциональному увеличению как масштабного коэффициента k02
min
, так и ![]() . Кроме этого, для реализации
. Кроме этого, для реализации ![]() необходимость увеличения k02
(k2
) при ограниченном пределе
необходимость увеличения k02
(k2
) при ограниченном пределе ![]() (27), как видно из (34), значительно увеличивает собственный шум всего устройства.
(27), как видно из (34), значительно увеличивает собственный шум всего устройства.
Снятие указанных структурных противоречий требует применения дополнительной общей отрицательной обратной связи и, следовательно, мультидифференциальных ОУ.
4. Синтез структур R -звеньев с дополнительными частотнозависимыми цепями
Как отмечалось выше, увеличение в R-фильтрах максимального уровня выходного напряжения связано с уменьшением коэффициента сдвига частоты полюса bz , что приведет к увеличению собственного шума схемы. Кроме этого, особенность схемотехнических решений ОУ в СВЧ диапазоне не позволяет использовать высокоомные резисторы в цепях местных и общей обратных связей, что существенно увеличивает потребляемый ток. Следует также отметить, что в этом же диапазоне частот подложка, занимаемая RC-цепью первого порядка, не превышает геометрическую площадь ОУ. Таким образом, и это можно показать достаточно строго, повышение многих показателей качества возможно путем использования в качестве частотозадающих цепей не только частотных свойств скорректированных ОУ, но и традиционных RC-цепей.
Предварительно отметим, что базовый вывод о невозможности построения ФВЧ и заграждающих фильтров в этом случае также сохраняется. Таким образом, для построения звеньев как полосового фильтра, так и фильтра нижних частот необходимо использовать один ОУ и RC-цепь первого порядка. Тогда для звена полосового типа:
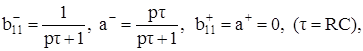 (37)
(37)
а для ФНЧ
 (38)
(38)
Принципиальные схемы таких звеньев приведены на рис. 4.
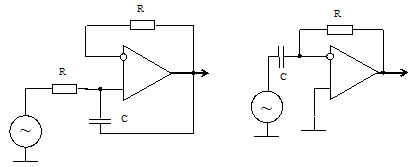
а) б)
Рис. 4. Принципиальные схемы звеньев второго порядка
с дополнительными частотозадающими цепями:
а) ФНЧ; б) ПФ
Анализ схем приводит к следующим результатам:
– для ФНЧ
 , (39)
, (39)
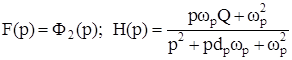 ; (40)
; (40)
– для звена ПФ
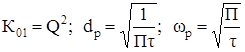 , (41)
, (41)
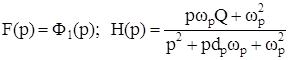 . (42)
. (42)
Таким образом, уровни динамических диапазонов звеньев определяются следующими соотношениями:
![]() , (43)
, (43)
![]() . (44)
. (44)
Поэтому
![]() (45)
(45)
звеньев с дополнительными цепями в ![]() раз больше, чем в R-фильтрах.
раз больше, чем в R-фильтрах.
В качестве примера реализации звена второго порядка с единственным конденсатором (RC/2-звенья) рассмотрим полосовой фильтр на базе ОУ с указанными в табл. 2 параметрами. На рис. 5 приведены результаты моделирования схемы для различной добротности. Как видно из соотношений (41), это достигается изменением постоянной времени RC-цепи (рис. 4б) в относительно широких пределах.
Для указанного набора параметров полоса звена – ![]() и Q выполнено моделирование схем во временной области (рис. 6, 7, 8) при подаче различных уровней гармонического сигнала в полосе пропускания. Анализ длительности переходных процессов показывает, что схема остается линейной при условии, что выходное ее напряжение не превышает граничное напряжение ОУ (табл. 2). Однако различия скорости нарастания выходного напряжения (
и Q выполнено моделирование схем во временной области (рис. 6, 7, 8) при подаче различных уровней гармонического сигнала в полосе пропускания. Анализ длительности переходных процессов показывает, что схема остается линейной при условии, что выходное ее напряжение не превышает граничное напряжение ОУ (табл. 2). Однако различия скорости нарастания выходного напряжения (![]() ) ограничивают максимально достижимое выходное напряжение схем. Основные характеристики звена приведены в табл. 4.
) ограничивают максимально достижимое выходное напряжение схем. Основные характеристики звена приведены в табл. 4.
электронный усилитель частотный операционный
Таблица 4
Основные характеристики RC /2-звена полосового типа
(%) |
(МГц) |
(%) |
Q |
(%) |
(мВ) |
(дБ) |
|
| 30,55 | 1 | 364 | 10 | 10,8 | 49 | 82 | 45 |
| 12,74 | 45 | 484 | 6,2 | 6,66 | 37 | 82 | 40 |
| 4,73 | 56 | 657 | 13,3 | 3,55 | 14 | 100 | 36 |
| Примечание. |
|||||||
Приведенные в табл. 4 погрешности реализации основных параметров связаны, как показывают дополнительные исследования, с влиянием паразитной входной емкости и вторым полюсом промежуточного каскада ОУ. Это, в частности, подтверждается результатами моделирования схемы звена ФНЧ (рис. 4а), где в силу параллельности основного каскада обратной связи аналогичные отклонения достигают 100 %, а влияние выходного сопротивления существенно уменьшает гарантированное затухание схемы в полосе заграждения.
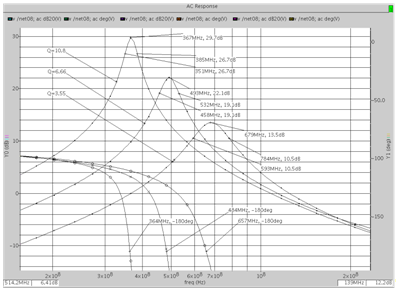
Рис. 5. Частотные характеристики RC/2-звена полосового типа
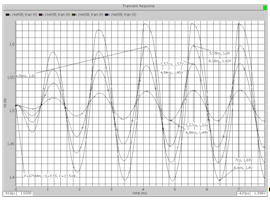
Рис. 6. Реакция схемы при Q=3,55 на различные уровни
входного гармонического воздействия
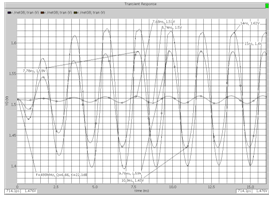
Рис. 7. Реакция схемы при Q = 6,66 на различные уровни
входного гармонического воздействия
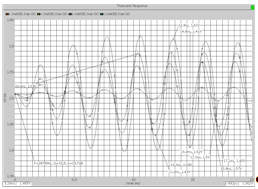
Рис. Реакция схемы при Q = 10,8 на различные уровни
входного гармонического воздействия
5. Синтез ФНЧ третьего порядка с дополнительными RC -цепями
Фильтры нижних частот в СВЧ диапазоне образуют отдельный и важный в практическом отношении класс устройств частотной селекции. Достаточно отметить каналообразующие фильтры при синхронной обработке сложных радиотехнических сигналов. В этом случае необходимо не только подавление амплитуд суммарных гармонических составляющих, но и обеспечение линейной фазочастотной характеристики в рабочем диапазоне частот. В общем случае такие фильтры могут быть построены путем каскадирования звеньев второго и первого порядков, однако в ряде практически важных устройств (например, СФ блоков) относительно высокие качественные показатели обеспечиваются применением только одного ОУ с дополнительной RC-цепью второго порядка. При таком подходе получим
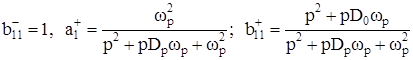 , (46)
, (46)
где D0 , Dp – затухание нуля и полюса пассивной цепи.
Структура локальной передачи ![]() имеет относительно простую физическую трактовку. Коэффициент при операторе p обеспечивает, как и в обычных RC-звеньях, компенсацию потерь в пассивной цепи и, следовательно, потенциальное увеличение добротности (Q). Именно такие свойства цепи без дополнительных структурных мер в реальных фильтрах и приводят к пропорциональному Q сдвигу граничной частоты, обусловленному влиянием площади усиления ОУ. Для исключения этой зависимости в структуре
имеет относительно простую физическую трактовку. Коэффициент при операторе p обеспечивает, как и в обычных RC-звеньях, компенсацию потерь в пассивной цепи и, следовательно, потенциальное увеличение добротности (Q). Именно такие свойства цепи без дополнительных структурных мер в реальных фильтрах и приводят к пропорциональному Q сдвигу граничной частоты, обусловленному влиянием площади усиления ОУ. Для исключения этой зависимости в структуре ![]() используется дополнительный член p2
, который и позволяет получить необходимые для решения общей задачи параметрические степени свободы. Принципиальная схема такого звена показана на рис. 9.
используется дополнительный член p2
, который и позволяет получить необходимые для решения общей задачи параметрические степени свободы. Принципиальная схема такого звена показана на рис. 9.

Рис. 9. Принципиальная схема ФНЧ третьего порядка R2C/3 типа
Анализ схемы позволяет определить набор базовых передаточных функций:
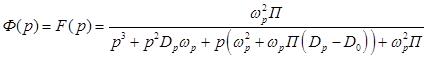 , (47)
, (47)
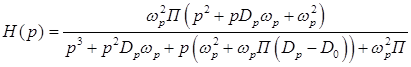 . (48)
. (48)
Введем нормировку оператора для перехода к НЧ-прототипу
![]() (49)
(49)
и коэффициент сдвига частоты
 , (50)
, (50)
получим
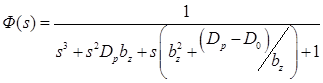 , (51)
, (51)
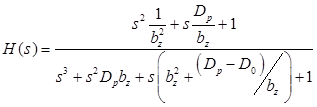 . (52)
. (52)
В диапазоне рабочих частот для АЧХ без явно выраженных пульсаций
![]() , (53)
, (53)
а
![]() (54)
(54)
Таким образом, динамический диапазон схемы определяется следующим соотношением:
![]() (55)
(55)
и в основном зависит от возможности минимизации численного значения затухания полюса Dp .
Оценим возможность создания на базе настоящей схемы ФНЧ с линейной фазовой характеристикой. Решение классической аппроксимационной задачи приводит к следующему положению полюсов передаточной функции (51):
![]() . (56)
. (56)
Следовательно, ее коэффициенты должны принимать значения
![]() , (57)
, (57)
при этом граничная частота 0 будет определяться частотой полюса пассивной цепи р и площадью усиления П. Для решения задачи необходимо найти соотношения между резистивными и емкостными элементами схемы. Учитывая, что
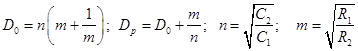 , (58)
, (58)
совместное решение (55) и (56) приводит к следующему результату:
![]() , (59)
, (59)
поэтому, как это видно из (49), (50) и (54), (55),
![]() . (60)
. (60)
Указанные параметры достаточно близки к оптимальным, т.к. минимальное значение затухания полюса пассивной цепи Dp
мин
= 3 [6]. Именно поэтому при проектировании указанных фильтров необходимо ориентироваться на ОУ, входные каскады которых имеют относительно большое граничное напряжение ![]() .
.
Результаты исследования принципиальной схемы ФНЧ третьего порядка на ОУ (табл. 2) с линейной ФЧХ в полосе пропускания приведены в табл. 5.
Таблица 5. Основные параметры ФНЧ R 2 C /3 с линейной ФЧХ
(%) |
(ГГц) |
(%) |
(град) |
(мВ) |
(дБ/окт) |
|
| 1 | 1,5 | 1,17 | 9,9 | 1,8 | 50 | 12 |
| Примечание. |
||||||
Отметим, что схема относительно легко настраивается на заданный закон ФЧХ в полосе пропускания изменением емкости конденсатора С2, при этом сохраняется требуемая форма АЧХ в широком диапазоне частот.
В анализируемом фильтре указанные в табл. 5 погрешности обусловлены влиянием входных емкостей и второго полюса ОУ. Однако, если в звене (рис. 4а) влияние указанных паразитных параметров оказывается значительным, то в схеме ФНЧ третьего порядка частотная зависимость входной проводимости четырехполюсника обратной связи в диапазоне высоких частот существенно уменьшает соответствующую параметрическую чувствительность. Именно поэтому не только в полосе пропускания, но и в переходной области частот параметры фильтра близки к ожидаемым.
Базовая альтернатива рассмотренному ФНЧ связана с уменьшением числа емкостных элементов и, следовательно, с использованием дополнительного ОУ. Синтез структуры такого устройства выполняется по алгоритму при N=2 и в конечном итоге связан с реализацией следующего набора локальных передач пассивной цепи:
![]() . (61)
. (61)
Принципиальная схема ФНЧ третьего порядка, соответствующая указанным условиям, приведена на рис. 10.
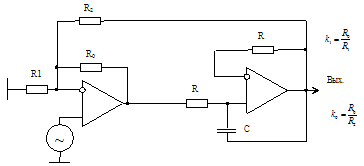
Рис. 10. Принципиальная схема ФНЧ третьего порядка RC/3 типа
Анализ схемы при указанном выше принципе частотной нормировки приводит к следующему результату:
![]() , (62)
, (62)
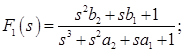 (63)
(63)
 , (64)
, (64)
где  , (65)
, (65)
 , (66)
, (66)
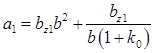 , (67)
, (67)
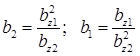 , (68)
, (68)
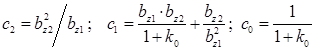 . (69)
. (69)
Виды передаточных функций (62)–(64) и структура коэффициентов (66)–(69) показывают, что при реализации АЧХ ФНЧ без «всплеска» коэффициента передачи вблизи 0 верхний уровень динамического диапазона определяется ОУ1, а собственный шум схемы – ОУ2:
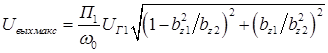 , (70)
, (70)
![]() . (71)
. (71)
Рассмотрим аналогично возможность построения ФНЧ с линейной фазовой характеристикой. Из (57) следует, что ![]() . Решение системы уравнений (65)–(67) приводит к следующему результату:
. Решение системы уравнений (65)–(67) приводит к следующему результату:
![]() , (72)
, (72)
что конкретизирует связь параметров ОУ и RC-цепи:
![]() (73)
(73)
Тогда, как это следует из (70) и (71), уровни динамического диапазона фильтра определяются следующими равенствами:
![]() . (74)
. (74)
Следовательно, при идентичных ОУ
![]() . (75)
. (75)
Таким образом, рассмотренные схемы ФНЧ при реализации фильтра с линейной ФЧХ (см. (60)) обеспечивают практически одинаковый динамический диапазон, однако максимальное выходное напряжение схемы с одним ОУ практически на 30 % больше.
Полученные результаты показывают, что недостатком рассматриваемого класса фильтров является относительно высокая параметрическая чувствительность к паразитным параметрам ОУ. Более детальное исследование позволяет утверждать, что температурные коэффициенты пассивных RC элементов не позволяют компенсировать возникающие под действием ОУ изменения не только АЧХ, но и ФЧХ в полосе пропускания. Именно поэтому одним из способов решения общей задачи построения прецизионного фильтра является создание более высокочастотных преобразователей напряжения со стабильной частотой единичного усиления.
Полученные результаты позволяют сделать достаточно важные для схемотехники СФ блоков с узлами частотной селекции выводы.
Во-первых, структуры с собственной и взаимной компенсацией уменьшают требования к активным элементам.
Во-вторых, собственная компенсация позволяет повысить общую стабильность характеристик устройства частотной селекции. Чувствительность основных параметров фильтра к нестабильности всех компонентов схемы не превышает 0,5, а при С1 =С2 чувствительность добротности к этим параметрам нулевая, что можно использовать, в частности, и для функциональной настройки звена на заданную частоту полюса.
Наконец, и это самое главное, работоспособность в ВЧ и СВЧ диапазонах схем с собственной и взаимной компенсацией является важным аргументом для широкого внедрения в соответствующих СФ блоках узлов и устройств с комплексом обратных связей, направленных на обеспечение необходимых функциональных зависимостей как СФ блоков, так и СнК в целом.
Библиографический список
1. Максимович, Н.Г. Методы топологического анализа электрических цепей [Текст] / Н.Г. Максимович. – Львов : Изд-во Львовского ун-та, 2010. – 258 с.
2. Масленников, В.В. Избирательные RC-усилители [Текст] / В.В. Масленников, А.П. Сироткин. – М. : Энергия, 2010. – 215 с.
3. Мееров, М.В. Синтез структур систем автоматического регулирования высокой точности [Текст] / М.В. Мееров. – М. : Наука, 2007. – 423 с.
4. Немудров, В.Г. Системы на кристалле. Проектирование и развитие [Текст] / В.Г. Немудров, Г. Мартин. – М. : Техносфера, 2008. – 216 с.
5. Остапенко, А.Г. Анализ и синтез линейных радиоэлектронных цепей с помощью графов [Текст] / А.Г. Остапенко. – М. : Радио и связь, 2009. – 280 с.
6. Прокопенко, Н.Н. Архитектура и схемотехника быстродействующих операционных усилителей [Текст] / Н.Н. Прокопенко, А.С. Будяков. – Шахты : Изд-во ЮРГУЭС, 2006. – 230 с.
7. Прокопенко, Н.Н. Архитектура и схемотехника с собственной и взаимной компенсацией импедансов [Текст] / Н.Н. Прокопенко, Н.В. Ковбасюк. – Шахты : Изд-во ЮРГУЭС, 2007. – С. 325.
8. Прокопенко, Н.Н. Быстродействующий СВЧ-операционный усилитель с нелинейной токовой обратной связью [Текст] / Н.Н. Прокопенко, А.С. Будяков, Н.В. Ковбасюк // Актуальные проблемы твердотельной электроники и микроэлектроники : труды 10-й Междунар. науч. конф. и школы-семинара. – Таганрог, 2006. – Ч. 2. – С. 161–164.
9. Прокопенко, Н.Н. Нелинейная активная коррекция в прецизионных аналоговых микросхемах [Текст] / Н.Н. Прокопенко. – Ростов н/Д. : Изд-во СКНЦ ВШ, 2010. – 224 с.
10. Свирщева, Э.А. Алгоритм и программа синтеза RC-схем с операционными усилителями в дифференциальном включении [Текст] / Э.А. Свирщева, А.И. Минаев // Избирательные системы с обратной связью. – Таганрог, 2008. – Вып. 4. – С. 185–186.
11. Сигорский, В.П. Проблемная адаптация систем автоматизированного проектирования [Текст] / В.П. Сигорский // Автоматизация проектирования в электронике. – Киев : Техника, 2009. – Вып. 26. – С. 3–14.
12. Синтез активных RC-цепей. Современное состояние и проблемы [Текст] / под ред. А.А. Ланнэ. – М. : Связь, 2009. – С. 296.
13. Старченко, Е.И. Мультидифференциальные операционные усилители [Текст] / Е.И. Старченко // Проблемы современной аналоговой микросхемотехники : сборник трудов МНПС. – Шахты, 2007. – С. 35–42.
14. Тафт, В.А. Спектральные методы расчета нестационарных цепей и систем [Текст] / В.А. Тафт. – М. : Энергия, 2008. – 272 с.
15. Торговников, Р.А. Приборно-технологическое моделирование SiDe биполярных и МОП-транзисторов структур СБИС [Текст] / Р.А. Торговников // Проблемы разработки перспективных микроэлектронных систем : материалы Всерос. науч.-техн. конф. – Подмосковье, 2006. – С. 173–178.
16. Фаддеева, В.И. Вычислительные методы линейной алгебры [Текст] / В.И. Фаддеева, Д.К. Фаддеев. – М. : Физматгиз, 2009. – 655 с.
17. Филаретов, Г.А. Организация структуры критериев в задачах векторной оптимизации радиотехнических цепей и систем [Текст] / Г.А. Филаретов, Л.Б. Шустерман, Т.В. Мазюкевич // Информатика. Сер. Автоматизация проектирования. – 2007. – Вып. 3. – С. 45–54.
18. Чибизов, Д.Г. Автоматизация процедур поиска решений при структурном синтезе нестационарных ARC-схем с расширенным частотным и динамическим диапазонами [Текст] / Д.Г. Чибизов // Интеллектуальные САПР. Тем. вып. Известия ТРТУ. – 2009. – № 3. – С. 224–228.
19. Чибизов, Д.Г. Структурный синтез гибридных фильтров Калмана-Бьюси [Текст] : дис. … канд. техн. наук / Чибизов Д.Г. – Таганрог, 1999. – 202 с.
20. Штойер, Р. Многокритериальная оптимизация [Текст] / Р. Штойер. – М. : Радио и связь, 2008. – 504 с.
21. Akerberg, D. A versative RC building block with inherent compensation for the finite bandwidth of the amplifier / D. Akerberg, К. Mossberg // IEEE Trans. – 2007. – V. CAS-21. – Р. 75–78.
22. Applications handbook. Burr-Brown Corp. – 1994. – Р. 425.
23. Brackett, P. Active compensation for high frequensy effects in op-amp circuits with applications to active RC-filters / Р. Brackett, А. Sedra // IEEE Trans. – 2006. – V. CAS-23, № 2. – Р. 68–72.
24. Cauer, W. Theory der linearen Weehselstrom-shaltung / W. Gauer // Akademic-Verlag. – 2009. – 770 s.
25. Design-in reference manual // Analog Devices, Inc. – 2008. Р. 9–3–9-569.
26. Krutchinsky, S.G. Structurallytopologicalprinciplesofself-compensationinelectronicdevices / S.G. Krutchinsky, N.N. Prokopenko, E.I. Starchenko // Proceeding ICCSC`04. – Moscow, Russia, 2007. – Р. 26–30.
27. Goldberd, D. Genetic Algorithms in search optimization and Machine Leorning / D. Goldberd // Addision-Wessley Publishing Company. Inc. – USA, 2009.
28. Mitra, S.K. Fundamental limitation of active filters / S.K. Mitra, M.A. Soderstrand // Proc. of 4-th colloquim on microwave communication. – Budapest, 2010.
29. National Semiconductor Application Note OA-11, A Tutorial on Applying OpAmps to RF Applications [Электронныйресурс] / Сайткомпании National Semiconductor, September, 2008. – URL : http://www.national.com/an/OA/OA-11.pdf, своб.
30. Sandberg, I.W. On the theory of linear multiloop feedback systems / I. W. Sandberg // BSTJ. – 2011. – V. 42, № 53. – Р. 355–382.
31. Soderstrand, M.A. Design of active filters with zero passive Q-sensitivity / M.A. Soderstrand, S.K. Mitra // IEEE Trans. on circuit theory. – 2008. –№ 3.
32.  Vlach, J. The influence of the limited bandwidth of active elements on active filters / J. Vlach // Proc., Nat. Electron Conf, Chicago. III. – 2009. – Р. 449–453.
Vlach, J. The influence of the limited bandwidth of active elements on active filters / J. Vlach // Proc., Nat. Electron Conf, Chicago. III. – 2009. – Р. 449–453.