Техника интегрирования и приложения определенного интеграла
СОДЕРЖАНИЕ: Способы определения точного значения интеграла по формуле Ньютона-Лейбница и приближенного значения интеграла по формуле трапеций. Порядок нахождения координаты центра тяжести однородной плоской фигуры ограниченной кривой, особенности интегрирования.Контрольная работа
по теме «Техника интегрирования и приложения определенного интеграла»
№ 314
Найти неопределенные интегралы:
![]()
![]()
![]()
№ 335
Найти определенный интеграл:
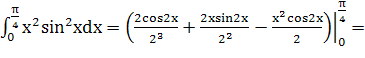
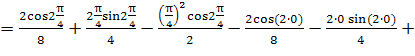
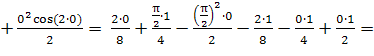
![]()
№ 356
Найти:
1. точное значение интеграла по формуле Ньютона-Лейбница;
2. приближенное значение интеграла по формуле трапеций, разбивая отрезок интегрирования на 8 равных частей и производя вычисления с округлением до 4 десятичных знаков;
3. относительную погрешность.
Решение:
1.
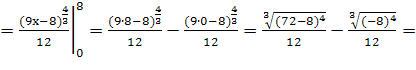
![]()
2.![]()
![]()
![]() , где
, где
![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]()
![]()
№ 377
![]()
![]()
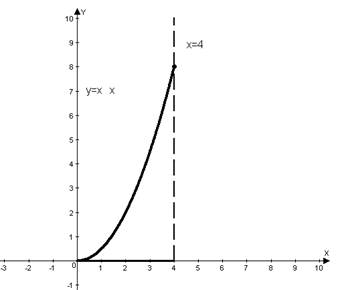
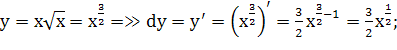
Пределы интегрирования по x от 0 до 4:
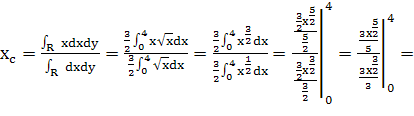
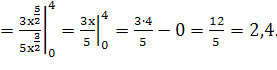
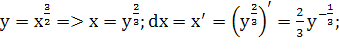
Пределы интегрирования по y от 0 до 8:
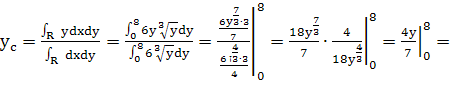
![]()
Координаты центра тяжести данной фигуры (2,4; 4,6).
№ 398
Вычислить несобственный интеграл или установить его расходимость:
![]()
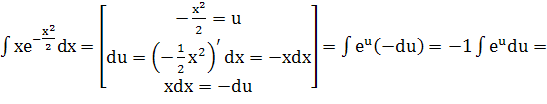
![]()
![]()
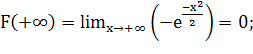
![]()
Несобственный интеграл вычислен и равен 1, следовательно он сходится.
№451
1. построить на плоскости хОу область интегрирования;
2. изменить порядок интегрирования и вычислить площадь области при заданном и измененном порядках интегрирования;
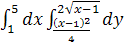
Решение:
1. Пределы внешнего интеграла по переменной х – числа 1 и 5 указывают на то, что область D ограничена слева прямой х = 1 и справа х = 5.
Пределы внутреннего интеграла по переменной у – указывают на то, что область D ограничена снизу параболой ![]() и сверху линией
и сверху линией ![]() .
.
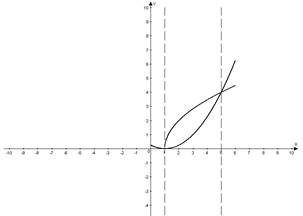
2. Чтобы изменить порядок интегрирования, установим пределы интегрирования для внешнего интеграла по переменной у. Как видно из рисунка, наименьшее значение которое принимает у в точке А(1;0) равно 0, а наибольшее значение в точке В(5; 4) равно 4. Т.О. новые пределы интегрирования: 0 – нижний, 4 – верхний.
Определим пределы для внутреннего интеграла по переменной х. Выразим х из уравнений:
![]()
![]()
![]()
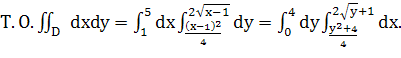
![]()
![]()
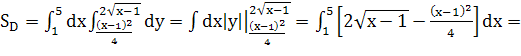
![]()
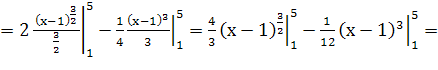
![]()
![]()
![]()
![]()
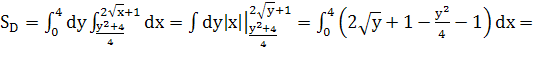
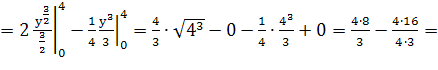
![]()