Технологія забезпечення якості фундаментальної підготовки майбутніх вчителів математики

СОДЕРЖАНИЕ: Технологія забезпечення якості фундаментальної підготовки майбутніх вчителів математики О.А. Чемерис Україна як європейська держава зробила важливий крок на шляху до інтеграції вищої освіти в загальноєвропейський простір. У контексті таких змін педагогічна освіта розглядається не лише як окрема унікальна сфера підготовки нової генерації вчителів, а як винятково важливий ресурс розвитку інтелектуального потенціалу нації.

Технологія забезпечення якості фундаментальної підготовки майбутніх вчителів математики

О.А. Чемерис

Україна як європейська держава зробила важливий крок на шляху до інтеграції вищої освіти в загальноєвропейський простір. У контексті таких змін педагогічна освіта розглядається не лише як окрема унікальна сфера підготовки нової генерації вчителів, а як винятково важливий ресурс розвитку інтелектуального потенціалу нації. Покращення якості вищої освіти, забезпечення рівного доступу до неї передбачено Законом України Про вищу освіту, постановою Кабінету Міністрів Концепція розвитку освіти в Україні та спрямоване на утвердження новітніх інформаційних технологій. Важливою умовою модернізації освіти є підвищення якості фундаментальної підготовки педагогічних працівників, яка є основою формування фахівця та оптимізує суспільний розвиток. Акцент у професійній підготовці переноситься з традиційного навчання на формування ключових компетенцій.

Однак якість фундаментальної підготовки майбутніх учителів не відповідає вимогам європейських стандартів. Особливо це стосується майбутніх учителів математики, оскільки система знань, умінь та навичок, якою оволодівають студенти фізико-математичного факультету, реалізується на високому рівні складності. Останнє зумовлює потребу узагальнення досвіду фундаментальної підготовки майбутніх учителів математики та вимагає оновлення її теоретико-методологічних засад для створення якісно нової моделі навчального процесу, яка б відповідала сучасним тенденціям розвитку системи педагогічної освіти.

Пошук нових шляхів удосконалення фундаментальної підготовки майбутніх учителів математики вимагає змін у процесі навчання. Як зазначають В.П. Беспалько [2], В.М. Єремєєва [15], Г.Ю. Ксьозова [16], М.В. Кларін [16], В.М. Максимова [13], І.Ф. Прокопенко [16], Г.К. Селевко [29], О.М. Столяренко [35], Д.В. Чернилевський [16], якість фундаментальної підготовки майбутніх фахівців прямо залежить від адекватно обраної й професійно реалізованої педагогічної технології, яке формує необхідне інформаційне середовище на основі активної педагогічної взаємодії викладача й студента.

Серед сучасних технологій підготовки спеціаліста-математика у світовій практиці найчастіше використовують наступні: інтелектуальні навчаючі системи [32], метод проектів [6], інформатизацію навчального процесу [8], експертні системи [22; 39], мультимедійні навчаючі системи [27], дистанційне навчання [21], технологію науково-методичного супроводу [3; 11; 33; 34] тощо.

У ході експериментальної роботи, що проводилась на базі фізико-математичного факультету Житомирського державного університету імені Івана Франка, основою побудови педагогічної технології забезпечення якості фундаментальної підготовки майбутніх учителів математики став науково-методичний супровід як перспективний напрям технологізації навчального процесу у вищій школі, теоретико-методологічні основи використання якого обґрунтовані в дослідженнях Н.І. Лісової [133], Т.М. Сорочан [34].

Поняття науково-методичного супроводу є відносно новою категорією, яка вперше введена в науковий обіг у Національній доктрині розвитку освіти в Україні у ХХІ ст. [24].

Тлумачний словник визначає супровід як дію зі значенням йти поруч або те, що супроводить певну дію, явище [5, с. 1012]. Термін супровід вживається в педагогіці дедалі частіше. О. Сухомлинська пише: Дитина, що формується, – не лише самостійний індивід, її ріст і розвиток потребують не тільки педагогічного знання, а й педагогічного супроводу [36, с. 5].

Поняття науково-методичного супроводу обґрунтовано в державних документах:

· у Концепції розвитку загальної середньої освіти (Розділ ІІ) зазначено: Діяльність організаційних структур на всіх рівнях управління загальноосвітнім навчальним закладом набуває рефлексивного характеру завдяки введенню моніторингового супроводу управління [9, с. 6];

· у розділі ІІ Положення про експертизу психологічного і соціологічного інструментарію, що застосовується в навчальних закладах Міністерства освіти і науки України також зустрічається термін супровід: ... Центри відповідно до покладених на них завдань ... надають консультативні послуги і здійснюють методичне супроводження матеріалів експертизи [23, с. 2-3];

· у доповіді В. Кременя на засіданні Академії педагогічних наук України зазначено: Утвердження особистісної орієнтації освіти, розробка й запровадження освітніх інновацій значно підвищують попит на соціально-психологічний супровід навчального процесу [19, с. 24].

Отже, різні педагогічні джерела роблять акцент на тому, що супроводжувати можна розвиток особистості, освітні процеси, інновації.

Термін науково-методичний супровід вживається також у російській педагогічній літературі (В. Богословський [3], О. Козакова [14], М. Певзнер [18], Н. Рибникова [26], Л. Хубер [40]). Учені зазначають, що науково-методичний супровід доцільно розглядати як сукупність різноманітних форм, технологічних дій, процедур, заходів, які забезпечують допомогу педагогічним працівникам у подоланні труднощів протягом усієї професійної діяльності. Ними визначено функції науково-методичного супроводу, серед яких виокремлюються навчальна, консультативна, психотерапевтична, адаптивна та коригуюча.

О. Козакова підкреслює гуманістичну сутність супроводу, його спрямованість на процес розвитку особистості, необхідність самої особистості [14, c. 117]. Під супроводом вона розуміє спеціальний вид допомоги суб’єкту, спрямований на запобігання та подолання проблем його розвитку. Важливим для нашого дослідження є висновок автора про те, що найважливішою характерною ознакою супроводу є суб’єкт-суб’єктна взаємодія.

На думку російських учених, результатом впровадження науково-методичного супроводу має бути якість професійної діяльності педагога, яка проявляється в його професійній компетентності та виявляється через новоутворення в тих, хто навчається [12].

Сутнісна характеристика терміна супровід обмежує безпосереднє втручання одного суб’єкта в діяльність іншого. За такої умови перевага віддається опосередкованій взаємодії обох сторін освітнього процесу, тобто учасники науково-методичного супроводу мають стати її рівноправними партнерами за умови наявності різного рівня наукової підготовки або опанування практичним досвідом.

Методологія науково-методичного супроводу ґрунтується на засадах відкритої освіти, яка відповідає стратегії розвитку та європейській орієнтації освіти України в цілому [28]. Відкрита освіта має ознаки складної системи з множинними шляхами розвитку. Відкрита освіта як соціальна система здійснює активний обмін інформацією з оточуючим середовищем, реагує на соціально-економічні зміни [34]. У системі освіти демократичного суспільства учасники педагогічного процесу опановують позицію суб’єктів, тобто активно реалізують своє само-: займаються самоосвітою, самовдосконалюються, прагнуть до творчого самовираження.

Зауважимо, що в педагогічній науці та практиці частіше використовувалось поняття науково-методичне забезпечення, яке, на нашу думку, більше спонукає до пасивного очікування готових рекомендацій та матеріалів, ніж до активної, цілеспрямованої взаємодії педагогів і студентів щодо їх розробки. Саме необхідність мотивації і залучення до цієї професійної взаємодії усіх суб’єктів освітнього процесу є основною передумовою створення нової технології забезпечення якості фундаментальної підготовки майбутніх учителів математики.

Т.М. Сорочан пропонує розглядати технологізацію навчального процесу на засадах науково-методичного супроводу багатофункціонально [34, c. 201]:

· як певну послідовність дій, які мають забезпечити конкретний результат;

· як педагогічну систему для визначення та приведення у відповідність мети, змісту, методів та взаємодії суб’єктів науково-методичного супроводу;

· як процес взаємодії суб’єктів щодо впровадження інновацій, які забезпечують новий рівень розвитку освіти. У процесі спільної творчої діяльності викладачі і студенти опрацьовують інновації, виробляють необхідні рекомендації, здійснюють моніторинг результатів.

Наше розуміння технології забезпечення якості фундаментальної підготовки майбутніх учителів математики, як нової педагогічної категорії, полягає в тому, що це є побудована поетапно професійно-педагогічна суб’єктна взаємодія освітнього процесу, необхідними умовами впровадження якої є добровільність і партнерство, визначальними ознаками – особистісний і професійний розвиток як викладачів, так і студентів, а результатом – якість фундаментальної підготовки майбутніх учителів математики.

Науковий зміст запропонованої технології полягає в тому, що, з одного боку, через її застосування викладачі впроваджують гнучкі алгоритми, які передбачають попереднє проектуваня фахової підготовки, що здійснюється в ході навчального процесу, та не усувають можливості реалізації педагогічного експерименту; з іншого – це такий проект фахової підготовки студентів-математиків, який зумовлює структуру і зміст спеціально організованого навчального процесу з врахуванням розвитку їх інтелектуальних можливостей та спрямованого на досягнення високого рівня якості освіти.

Розробка технології забезпечення якості фундаментальної підготовки майбутніх учителів математики здійснювалася на основі системного підходу, використання якого передбачає: 1) представлення моделі досліджуваного явища в межах усієї фахової підготовки майбутніх учителів математики, а не лише кожної окремої дисципліни; 2) врахування умов, що впливають на динаміку протікання досліджуваного явища; 3) вибір певних критеріїв оцінювання ефективності розробленої моделі [7].

У ході експериментальної роботи була вибрана така логіка втілення технології забезпечення якості фундаментальної підготовки майбутніх учителів математики:

1. Виділення загальної мети фундаментальної підготовки, а також кожної її складової, майбутніх учителів математики через показники, які можна діагностувати.

2. Визначення проміжних цілей фундаментальної підготовки майбутніх учителів математики, кожної її складової шляхом конкретизації попередньо визначених показників.

3. Добір та дидактичне обґрунтування змісту навчального процесу відповідно до поставленої системи цілей.

4. Реалізація змісту шляхом впровадження доцільних форм, методів, засобів, які забезпечені об’єктивними методиками контролю якості досліджуваного явища.

5. Поетапне (п. 1-4) врахування умов (факторів) забезпечення якості фундаментальної підготовки майбутніх учителів математики [7].

Таким чином, фундаментальну підготовку майбутніх учителів математики у визначеному дослідженням аспекті представимо згідно акмеологічного підходу у вигляді моделі технології, зміст якої реалізується на трьох рівнях: загальнопедагогічному, поетапному, предметних технологій.

Розглянемо більш детально кожен із них.

Загальнопедагогічний рівень функціонування технології забезпечення якості фундаментальної підготовки майбутніх учителів математики репрезентує цілісний освітній процес освітнього закладу певного напряму навчання. У такому вигляді розроблену технологію ототожнюють із педагогічною системою [7, с. 67].

У нашому випадку зазначений рівень відображає структурно-змістову наповненість фундаментальної підготовки майбутніх учителів математики в контексті державного замовлення через міжпредметні зв’язки спецдисциплін, визначених навчальним планом для спеціальності Педагогіка і методика середньої освіти. Математика і фізика та спецкурсів, що пропонуються студентам на вибір. Якість фундаментальної підготовки на визначеному рівні забезпечується також її логічним поєднанням з іншими видами професійної підготовки (психолого-педагогічною, інформаційно-технологічною, соціально-гуманітарною, практичною, методичною), що обумовлює цілісність професійно-педагогічної підготовки; усвідомленням взаємозв’язку зі змістом шкільних дисциплін як якісного результату її комплексного впровадження (див. рис. 1)

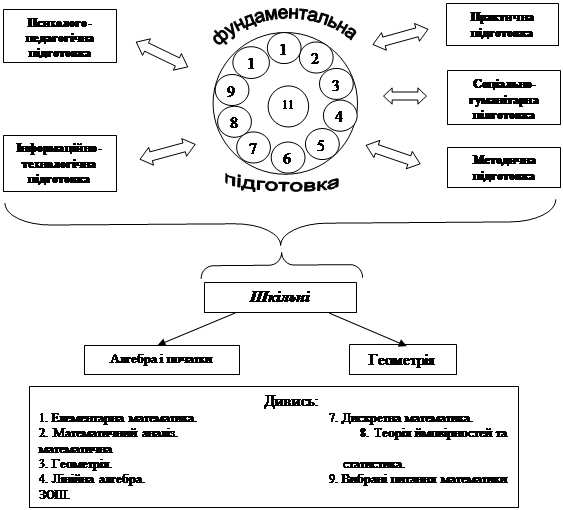
Рис. 1. Система фундаментальної підготовки майбутніх учителів математики (загальнопедагогічний рівень)

Поетапний рівень функціонування технології забезпечення якості фундаментальної підготовки майбутніх учителів математики передбачає окрему методику реалізації певного змісту навчання в межах одного предмета, групи предметів.

Як відомо, методика обумовлюється окремою дидактикою, яка враховує своєрідність змісту освіти й засобів її засвоєння. За сутнісною інтерпретацією поняття методика ширше, ніж поняття технологія (до якого належить науково-методичний супровід), адже воно включає і змістовий, і інструментальний аспект педагогічного процесу. Отже, методика є окремою теорією, а технологія – алгоритмом її втілення в практику [7, с. 67, 71].

Теоретичною основою побудови нашої технології стало поетапне забезпечення навчального процесу згідно з таксономічним (послідовне розташування) підходом Блума, в основу якого покладено просування того, хто навчається за рівнями засвоєння: І – базовий (знання); ІІ – інтерпретаційний (розуміння); ІІІ – реалізаційний (застосування); ІV – структурний (аналіз); V – інтегративний (синтез); VІ – підсумковий (оцінка) (див. рис. 2).

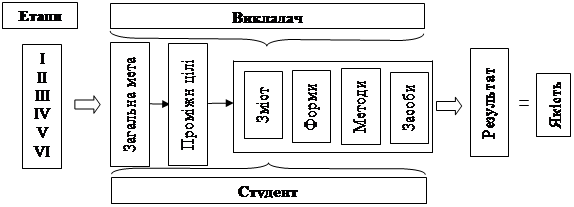Рис. 2. Поетапний рівень технології забезпечення якості фундаментальної підготовки майбутніх учителів математики

Перший етап зазначеного рівня умовно названо базовим. Його мета – запамятовування та відтворення матеріалу, що вивчається.

Головним завданням інтерпретаційного етапу є перетворення (трансляція) матеріалу з однієї форми вираження в іншу: інтерпретація матеріалу студентом (пояснення, короткий виклад тощо); передбачення подальшого ходу розгортання подій, явищ.

На етапі реалізації здійснюється вміння використовувати вивчений матеріал у конкретних умовах і нових ситуаціях.

Зазначені етапи (І-ІІІ) мають репродуктивний характер та створюють підґрунтя для переходу студента на рівень продуктивної (творчої) діяльності, що чітко окреслене наступними етапами-кроками (IV-VI): в основу структурного етапу покладено формування вмінь розбивати матеріал на складові так, щоб чітко окреслювалася його структура; інтегративного – вмінь комбінувати елементи для отримання цілого, якому притаманна новизна; підсумкового – вмінь оцінювати значення того чи іншого матеріалу (твердження, дослідження, дослідницьких матеріалів) з конкретною метою; оцінювати власні результати навчальної діяльності (якість) та результати навчальних досягнень своїх товаришів, колег.

За ознакою застосування рівень предметних технологій передбачає вдосконалення окремих предметів (підвищення якості їх викладання) шляхом оновлення певних частин навчального процесу, окремих курсів, конкретизації системи цілей у межах окремого предмета, використання спеціальних форм, методів, засобів, що забезпечують відповідний рівень якості фундаментальної підготовки [7, с. 67, 72].

Структуру предметної технології утворюють такі елементи:

а) концептуальна основа;

б) змістова частина, що включає:

· постановку, максимальне уточнення, формулювання цілей (загальних, проміжних, конкретних) щодо досягнення результатів;

· зміст навчального матеріалу;

в) процесуальна частина, до складу якої входять такі компоненти:

· організація навчального процесу відповідно до поставлених цілей шляхом застосування форм, методів та засобів навчальної діяльності;

· управління навчальним процесом (оцінювання поточних результатів; корекція навчання, спрямована на досягнення поставлених цілей;

· кінцева оцінка результатів [7, с. 70].

Подамо змістове наповнення предметної технології на прикладі проективної геометрії як складової фундаментальної підготовки майбутніх учителів математики.

Концептуальна основа побудови предметної технології чітко обґрунтована та окреслена на другому рівні технології забезпечення якості фундаментальної підготовки майбутніх учителів математики – поетапному навчанні. Саме вона й стала теоретичним підґрунтям технології викладання курсу проективної геометрії.

Найважливішим і при цьому найменш сформованим компонентом у представленій структурі технології є цілепокладання. Як правило, недостатній рівень якості навчання обумовлений невизначеністю, розпливчастістю, загальним характером цілей.

Ефективність цілепокладання визначається ступенем відповідності між результатами навчання й поставленими цілями, тому цілі мають бути:

· реальні, такі, яких можна досягти (вказувати на конкретні результати навчання);

· інструментальні, технологічні (визначати конкретні дії щодо їх досягнення);

· діагностичні (піддаватися виміру, визначенню їх відповідності з результатами навчальної діяльності [17, с. 102].

Технологія ефективного цілепокладання, розроблена Б. Блумом, пропонує шляхи визначення цілей, що передбачають ступінь їх ефективності з точки зору їх спрямованості на конкретні результати навчання. Таким чином, найбільш реальним, інструментальним і діагностичним є спосіб формулювання цілей через результати навчання, виражені в конкретних діях студента. Подамо зміст загальних і проміжних цілей для заданої предметної технології, спираючись на сутнісну характеристику науково-методичного супроводу, для студентів і викладачів окремо. За таких умов нарощування навчального потенціалу передбачає наявність різного характеру діяльності викладача і студента.

Наведемо поетапний розподіл освітніх цілей предметної технології курсу Проективна геометрія здійснено на основі узагальнення існуючих у педагогічній практиці способів постановки цілей за Б. Блумом (див. табл. 1) та представлено в табл. 2.

Таблиця 1

Категорії навчальних цілей в когнітивній області (за Б. Блумом)

Основні категорії навчальних цілей	Приклади узагальнених типів навчальних цілей
1. Знання – запамятовування й ре-продукція матеріалу, що вивчається.	Студент знає: терміни, що вживаються; конкретні факти; методи й процедури; основні поняття, правила та прийоми
2. Розуміння – перетворення (транс-формація) матеріалу з однієї форми вираження в іншу: інтерпретація матеріалу студентом (пояснення, короткий виклад); уявлення про подальший перебіг явищ, подій	Студент : розуміє факти, правила й принципи; інтерпретує схеми, графіки, діаграми; перетворює словесний матеріал у математичні вирази
3. Застосування – вміння вико-ристовувати вивчений матеріал в конкретних умовах і нових ситуаціях	Студент : застосовує закони, теорії в конкретних практичних ситуаціях, демонструє правильне застосування методу чи процедури, використовує поняття й принципи в нових ситуаціях
4. Аналіз – уміння розбити матеріал на складові так, щоб виразно виступала його структура	Студент : виділяє приховані (неявні) припущення, бачить помилки й недоліки в логіці роздумів, проводить відмінності між фактами й наслідками, оцінює значимість даних
5. Синтез – вміння комбінувати еле-менти, щоб отримати ціле, що містить новизну	Студент : пише творчі роботи, пропонує план проведення експерименту, використовує знання з різних галузей, щоб скласти план розвязання тієї чи іншої проблеми
6. Оцінка – вміння оцінювати зна-чення того чи іншого матеріалу (доведення, художнього твору, дослідження, дослідницьких даних) для конкретної мети	Студент : оцінює логіку побудови матеріалу у вигляді письмового тексту, оцінює відповідність висновків до наявних даних, оцінює важливість того чи іншого продукту діяльності, виходячи з внутрішніх критеріїв, оцінює значимість того чи іншого продукту діяльності, виходячи із зовнішніх критеріїв якості

[17, c. 37]

Таблиця 2

Категорії освітніх цілей предметної технології курсу Проективна геометрія (загальний підхід)

Етапи	Загальна мета		Проміжні (конкретні) цілі
	Викладач	Студент	Викладач	Студент
Репродуктивні етапи	І – базовий (знання)	Передає зміст навчальної фундаментальної дисципліни	Знає предмет, мету, завдання навчальної фундаментальної дисципліни та відтворює її зміст	- окреслює та конктеризує зміст навчання; - описує та акцентує увагу на теоретичних основах для обгрунтування дидактичної проблеми; - перевіряє надані знання	- знає геометричні об’єкти, основні математичні поняття, означення, теореми; - відтворює письмово й усно як окремі теми, так і весь матеріал в цілому
	ІІ – інтерпретаційний (розуміння)	Учить інтерпретувати викладений матеріал	Розуміє значення вивченого матеріалу, усвідомлює наявні міжпредметні зв’язки з іншими науками	- конкретизує математичні факти та явища, змістовно їх узагальнює; - прогнозує результати підготовки студентів на даному етапі; - обґрунтовує відповідні критерії, за якими можна відстежити результат на даному етапі	- адаптує викладений матеріал, виділяє в ньому головне та відрізняє другорядне; - пояснює внутрішні й зовнішні взаємозвязки в межах теми, розділу, навчальної дисципліни
Репродуктивні етапи	ІІІ – реалізаційний (застосування)	Впроваджує заходи щодо ефективного застосування знань на репродуктивному рівні	Оперує теорією для розв’язування завдань репродуктивного характеру	- пропонує завдання репродуктивного характеру; - органічно включає в навчальнй процес механізми аналізу, синтезу; - допомагає при виникненні труднощів; - уживає заходи щодо оптимізації навчального процесу на заняттях	- розв’язує завдання відтворюючого характеру; - уміє визначати типи завдань, які розв’язуються за допомогою вивчених понять; - демонструє отримані знання на практиці
Пошукові етапи	ІV – структурний (аналіз)	Створює умови для обробки поданої інформації	Вміє порівнювати, зіставляти й синтезувати інформацію; оцінювати як сам процес, так і результат; обґрунтовувати й міркувати; передбачає наслідки; перегруповує ідеї та зв’язки	- наштовхує на диференціацію інформації, підкреслюючи внутрішні зв’язки; - навчає розпізнавати поняття та підводити свої дії під них; - допомагає виявити помилки в міркуваннях; - пояснює власну позицію	- виділяє структуру поданого матеріалу; - розпізнає помилки в логічних міркуваннях; - формує у власній професійній діяльності систему цінностей на основі їх глибого осмислення
Пошукові етапи	V – інтегративний (синтез)	Створює умови для діяльності на інтегративному рівні	Порівнює шкільні дисципліни з фундаментальни-ми, створює власні наробки щодо майбутньої професії, подає своє бачення процесу засвоєння теоретичних знань та вироблення професійних умінь	- генерує ідеї та наштовхує студентів на подачу вивченого матеріалу; - називає сучасні математичні проблеми і вказує можливі шляхи їх розв’язання	- пише творчі математичні роботи; - складає схеми, опори, які відтворюють теоретичний матеріал теми, розділу, курсу навчальної дисципліни; - самостійно виділяє проблеми в науці, осмислює їх і розв’язує
	VI – підсумковий (оцінка)	Створює умови для оволодіння вміннями оцінювати себе й товаришів	Оцінює власні результати й результати діяльності товаришів	- покладає власні повноваження на студентів; - виступає арбітром, пропонує об’ктивні критерії; - підводить підсумки	- критикує себе та інших: відповіді щодо викладу теорії, методи розвязання задач, оформлення творчих математичних робіт тощо; - вибирає власну систему педагогічних цінностей, ціннісного ставлення до різноманітних підходів у розвитку математичної науки; - пропонує власну концепцію майбутнього вчителя математики

Така побудова дає можливість посилити взаємозв’язок між цілями й наявним плануванням викладачем конкретних результатів навчання, а також забезпечує можливість декомпозиції (переведення) викладачем цілей навчання в конкретні навчальні задачі.

Подана таксономія навчальних цілей – інструмент, що дозволяє викладачу спланувати цілі навчання за конкретним розділом, темою, визначити еталон засвоєння матеріалу (якості) та рекомендувати його студентам.

Така постановка цілей дає можливість також за рахунок субєкт-субєктної взаємодії, на якій будується технологія науково-методичного супроводу, врахувати в ході реалізації навчального процесу педагогічні умови, що впливають на процес фундаментальної підготовки майбутніх учителів математики.

Зміст навчального матеріалу

Цілі фундаментальної підготовки в цілому та її окремих курсів зокрема визначають зміст навчального матеріалу, яким має оволодіти студент.

Сучасна дидактика розрізняє поняття зміст освіти і зміст навчання. Змістом освіти називають той рівень особистісного розвитку, предметної й соціальної компетентності людини, яким вона оволодіває в результаті здобуття освіти [10, c. 98]. Таким чином, зміст освіти складають система знань, умінь, навичок, рис творчої діяльності, світоглядних і поведінкових якостей особистості, які обумовлені вимогами суспільства й для досягнення яких необхідно спрямувати зусилля тих, хто навчає, й тих, хто навчається.

На рівні загального теоретичного розуміння зміст освіти, визначений державним освітнім стандартом, являє собою сукупність вимог до рівня якості професійної підготовки спеціаліста, відображених у нормативних документах.

На відміну від цього, зміст навчання розглядають як педагогічно обґрунтований, логічно упорядкований, фіксований в навчальній документації (програмах, підручниках) та необхідний для обов’язкового вивчення навчальний матеріал, що визначає зміст діяльності викладача й пізнавальної діяльності студентів [17, с. 107].

Прийнято виділяти декілька основних рівнів змісту освіти: рівень загального теоретичного уявлення, рівень навчальної дисципліни, рівень навчального матеріалу [20].

Завданням нашого дослідження є розробка доцільного змісту навчального матеріалу конкретної дисципліни, що сприятиме підвищенню якості його викладання й фундаментальної підготовки в цілому.

Спираючись на роботи В.П. Беспалько [2], В.В. Попова [17], в дослідженні враховувались такі загальні вимоги до відбору змісту навчання спеціальних (фундаментальних) дисциплін:

1. Зміст спеціальної дисципліни має бути структурований відповідно до логіки побудови системи майбутньої професійної діяльності фахівця, орієнтований на теоретичні основи дій, прийомів, операцій, процесів усіх сфер професійної діяльності.

2. Основою визначення необхідності й достатності дидактичних одиниць навчального матеріалу повинна бути робоча навчальна програма, що передбачає розгляд визначень, класифікацій, порівняльних оцінок, дій майбутнього фахівця.

3. Теоретичні основи професійної діяльності, як предмет навчання, мають відображати сучасні досягнення в галузі науки.

4. Відбір змісту освіти має враховувати закономірності, принципи, технології педагогічного процесу, що гарантують реалізацію освітніх, розвивальних і виховних завдань.

5. Дедуктивна основа побудови змісту має забезпечувати його логіку (від загального до одиничного або від одиничного до загального).

6. При виборі змісту дисциплін фундаментальної підготовки необхідно враховувати його гуманістичну складову.

7. При відборі змісту навчальної дисципліни необхідно враховувати здібності тих, хто навчається, до продуктивної навчально-пізнавальної діяльності.

8. Експериментальна, дослідницька основа змісту предметів фундаментальної підготовки професійної педагогічної освіти потребує обліку необхідності проведення перетворень на кожному навчальному занятті, на всіх фазах кожного етапу. Весь педагогічний процес повинен являти собою дослідження, в якому беруть участь викладач-дослідник, студент-дослідник-початківець.

На думку І.Я. Лернера, зміст освіти має включати такі компоненти: систему наукових знань; способи діяльності в типових ситуаціях; досвід творчої діяльності; досвід емоційно-ціннісного ставлення до світу [17, с. 116]. Однак, цей склад елементів змісту освіти не визначає конкретний зміст знань і способів діяльності, що підлягають включенню в навчальні програми та підручники. З цією метою, як відзначає І.Я. Лернер, необхідно застосовувати й інші критерії: види знань, логіку науки й навчальної дисципліни, типи вмінь тощо [38, с. 79].

Фундаментальна підготовка майбутнього вчителя математики передбачає вивчення теоретичних основ спеціальності Математика. Фізика згідно з вимогами до рівня теоретичної підготовки педагогічного працівника відповідного профілю вищих педагогічних навчальних закладів та класичних університетів і базується на новітніх досягненнях науки. Для майбутнього вчителя математики згідно з навчальним планом, прийнятим Житомирським державним університетом імені Івана Франка, такими дисциплінами є елементарна математика, математичний аналіз, геометрія, лінійна алгебра, алгебра і теорія чисел, дискретна математика, диференціальні рівняння, теорія ймовірностей та математична статистика, вибрані питання елементарної математики, історія математики, ряд спецкурсів (основи векторного й тензорного аналізу, задачі з параметрами, основи наукових досліджень тощо).

Проаналізувавши навчальні плани та програми, розроблені кафедрами математики й математичного аналізу Житомирського державного університету імені Івана Франка, визначимо особливості фундаментальної підготовки на прикладі геометрії, математичного аналізу та алгебри й теорії чисел.

Діючі тематичні плани з вибраних дисциплін складені на основі раніше діючих програм із врахуванням сучасних вимог до загальноосвітньої і професійної підготовки вчителя математики, міжпредметних звязків і звязку із шкільним курсом математики, досвіду викладання в педагогічних вищих закладах освіти. Принципово вони відрізняються від попередніх більшою детальністю і гнучкістю, оскільки включають інваріантну обовязкову і варіативну на вибір кафедри, викладача частини, а також кількістю годин [25].

Наведемо порівняльну характеристику розподілу загальних годин для спеціальності Математика. Фізика згідно з навчальними планами Житомирського державного університету імені Івана Франка для основних (базових) математичних дисциплін (див. табл. 3).

Таблиця 3

Розподіл годин для математичних дисциплін

(спеціальність Математика. Фізика)

Навчальні роки	Статус навчального закладу	Математичний аналіз	Геометрія	Алгебра і теорія чисел
1993-1994 н.р.	педагогічний інститут	392	270	238
2000-2001 н.р	педагогічний університет	816	480	405
з 2004 р. по н.ч.	класичний університет	702	402	200

Збільшення на певному етапі кількості годин пояснюється включенням до навчальної дисципліни окремих питань сучасної науки (так, для математичного аналізу – теми з функціонального аналізу, для геометрії – питань основ геометрії тощо) та введенням як обовязкової самостійної контрольної роботи, написання якої передбачає самостійне опрацювання теоретичного матеріалу з самостійним розвязуванням задач. Частково зменшення годин з 2004 року повязане з їх перерозподілом між основними дисциплінами та введеними спецкурсами (для математичного аналізу та геометрії) або поділом дисципліни на дві самостійні (від алгебри й теорії чисел відокремлено лінійну алгебру).

Спираючись на запропоновані теоретичні положення та специфіку курсу Проективна геометрія, дамо характеристику змістового компонента предметної технології науково-методичного супроводу.

У цілому компонент являє собою систему особистісно-привласнених студентом фізико-математичного факультету якісних знань із фундаментальних дисциплін. Головною ознакою таких знань є багатофункціональність. Це не просто інформація, що пасивно зберігається в пам’яті, а засіб регуляції практичної діяльності, який полягає в нестандартному застосуванні засвоєних знань. Висока насиченість теоретичними знаннями, які включають в себе аксіоми, основні теореми, леми, правила з обов’язковою реалізацією їх через уміння й навички – це особливість змістового компонента, що розглядається.

Сама предметна галузь надає необмежені можливості для інтелектуального розвитку, тренування вмінь аналізувати, синтезувати, абстрагувати, класифікувати, систематизувати, узагальнювати, планувати, а відпрацьовані вміння можна з успіхом переносити зі світу абстракції у реальний світ.

Зміст навчальних предметів необхідно насичувати таким матеріалом, який буде сприяти послідовній багатоланковій диференціації когнітивних структур і їх подальшій інтеграції. Іншими словами, бажано, щоб навчальний матеріал мав потенційну можливість до диференціації й інтеграції інформації, тобто до збільшення елементів розумової діяльності (дій, операцій і пізнавальних результатів) з подальшим їх упорядкуванням, структурним ієрархізованим об’єднанням. Це може здійснюватися на рівні конкретизації й узагальнення, систематизації знань, класифікації понять тощо.

Наприклад, логічний каркас програми з геометрії складається з ряду розділів: аналітична геометрія на площині та в просторі, основи геометрії, конструктивна, проективна та диференціальна геометрії. Цей курс повинен створювати в студентів максимально повне і цілісне сприймання математичної науки (від Евкліда до наших часів).

Розглянемо зміст навчальних фундаментальних дисциплін на прикладі проективної геометрії.

У нині діючих підручниках з вищої геометрії для фізико-математичних спеціальностей вищих закладів освіти не завжди звертається увага на зв’язок університетського та шкільного курсів геометрії, який значною мірою сприяє покращенню якості фундаментальної підготовки майбутніх учителів математики. Особливо відчутною для студентів ця проблема стає при вивченні питань проективної геометрії, які найбільш відірвані від теорії та методики викладання геометрії в школі. Тому виникає потреба в такому викладанні теоретичних питань курсу проективної геометрії, який запропоновано в складеній навчальній програмі, розробленій на базі кафедри математики ЖДУ імені Івана Франка (див. табл. 4).

Таблиця 4

Навчальна програма курсу проективної геометрії

№ з\п	Тема	Лекції (год.)	Практ. (год.)
1	Проективний простір	3
2	Теорема Дезарга	2	2
3	Складне відношення чотирьох елементів форм І-го ступеня	2	4
4	Повний чотирьохвершинник	1
5	Проективна відповідність	3	2
6	Інволюція	4	2
7	Проективні перетворення форм ІІ-го ступеня	3
8	Перспективні колінеації й гомології	3	4
9	Проективна теорія кривих ІІ-го порядку	6	8
10	Полюси й поляри кривої ІІ-го порядку	3	2
11	Афінна і метрична геометрія з проективної точки зору	4
Контрольна робота		2
Усього		34	26

Завдання курсу проективної геометрії у вищому освітньому закладі – розширення та поглиблення знань студентів щодо геометричних перетворень, їх інваріантів, обґрунтування необхідності розширення евклідового простору введенням невласних елементів (точок, прямих, площин) та побудови проективного простору й проективної геометрії в цілому. Навчальна програма включає основні поняття та методи проективної геометрії, головним з яких є метод центральної проекції. Саме тому вивчення проективної геометрії починається з перетворення центральної проекції і проективних властивостей фігур, які зберігаються при довільних центральних проекціях. Запропонована концепція викладу курсу проективної геометрії дозволяє тісно пов’язати нові поняття й теореми проективної геометрії з матеріалом елементарної геометрії, що має важливе значення в системі фахової підготовки майбутніх учителів математики.

Взявши евклідовий простір за основний в побудові проективного простору ми відмовилися від аксіоматичного методу побудови геометрії. Центральне місце в програмі займають принципи двоїстості, теорема Дезарга, подвійне (складне) відношення, гармонізм, проективні відповідності форм першого ступеня (колінеації), проективна теорія кривих другого порядку. Детально розглянута з проективної точки зору побудова афінної і метричної геометрії, яка має безпосереднє відношення до курсу елементарної (шкільної) геометрії. Кожна із зазначених геометрій (афінна й метрична) визначається своєю групою (за означенням Клейна). У побудованій груповій класифікації проективних перетворень містяться афінна, метрична група і група рухів.

Поданий змістовий компонент відповідає цілям, що визначені потребами розвитку суспільства, науки, культури та особистості; проявляється у введенні до нього тих знань, умінь і навичок, які відповідають сучасному рівню розвитку соціуму, наукового знання й забезпечують можливості особистісного зростання майбутнього фахівця.

Безумовно, впровадження етапу предметних технологій технології забезпечення якості фундаментальної підготовки майбутніх учителів математики передбачає не тільки засвоєння змісту комплексу навчальних дисциплін, але й певну організацію педагогічного процесу, використання форм, методів, засобів, що забезпечують творчий розвиток, соціальне, культурне становлення студента, а також підвищують якість фундаментальної підготовки в цілому.

У сучасній дидактиці розроблена велика кількість форм , кожна з них розкриває ту або іншу сторону організації навчання.

У педагогічних джерелах термін форма використовується в різних тлумаченнях. Форма в перекладі з латинської означає зовнішній вигляд. Відповідно, форма навчання – це зовнішня сторона організації навчального процесу, що відображає спосіб організації діяльності тих, хто навчається, і залежить від: кількості тих, хто навчається; характеру взаємодії субєктів навчання; ступеня самостійності тих, хто навчається; специфіки педагогічної діяльності тощо.

У вищому закладі освіти функціонують різноманітні організаційні форми навчання: лекції, практичні заняття, науково-дослідна робота студентів (проблемні групи, олімпіади, науково-практичні конференції).

Поетапне управління фундаментальною підготовкою передбачає застосування різних типів лекцій, кожна з яких виконує певну роль на конкретному етапі навчання: репродуктивного рівня (вступна, тематична, оглядова) та продуктивного рівня (проблемна, лекція-візуалізація тощо).

Метою використання системи лекцій репродуктивного рівня є передача інформації в готовому вигляді, формування інтересу до проективної геометрії. Завдання викладача – методично правильний підбір джерел інформації для самостійного опрацювання. Так, вступна лекція має на меті дати студентам загальне уявлення про завдання всього курсу проективної геометрії, розкрити структуру, звязок з іншими розділами геометрії (аналітичною, конструктивною, диференціальною) та іншими дисциплінами. Головне завдання вступної лекції – сприяти розвитку в студентів інтересу до предмета з метою його творчого засвоєння. Тематична лекція присвячується розкриттю конкретної теми навчальної програми з конкретної дисципліни (наприклад, низка лекцій, присвячених теоремі Дезарга: Теорема Дезарга в просторі (пряма і обернена). Теорема Дезагра на площині. Двоїстость прямої і оберненої теореми Дезарга на площині тощо). Оглядові лекції читають студентам перед державними іспитами.

Метою лекцій продуктивного рівня є розвиток математичного мислення, ознайомлення з актуальними проблемами математики, розвиток професійної мотивації тощо. В ході проблемної лекції нове вводиться як невідоме, яке необхідно відкрити. Мета викладача, створивши проблемну ситуацію, – спонукати студентів до пошуків вирішення проблеми, крок за кроком підводячи їх до шуканого результату. Для цього новий теоретичний матеріал подається у формі проблемного завдання. В його умовах є суперечності, які потрібно знайти й розвязати. На нашу думку, саме такий тип лекції є доречним при вивченні перших тем програми курсу: Побудова евклідової моделі проективного простору, Великий та малий принцип двоїстості. Лекція-візуалізація виникла як результат пошуку нових можливостей реалізації принципу наочності. Матеріал подають усно, відтворюючи у візуальній формі. Демонстраційні матеріали виступають носіями змістової інформації, яка сприймається, усвідомлюється й може служити опорою адекватних думок і практичних дій. Наприклад, у допомогу викладачеві студентом пятого курсу фізико-математичного факультету Черкашиним І. була створена демонстраційна модель для побудови відповідних елементів проективної відповідності двох форм першого ступеня, точок кривої другого порядку за теоремою Паскаля, прямих пучка другого порядку за теоремою Бріаншона.

В основі лекцій зазначеного рівня лежить продуктивна інформація. Її створює студент на основі випередження її засвоєння, за таких умов він констатує знання й шляхи їх здобуття у власній свідомості. Для реалізації поставлених завдань викладач концентрує увагу студентів на проблемах, які необхідно розвязати на черговому лекційному занятті (принцип випереджального навчання). Головне – вміти правильно виявити, позначити й сформулювати ці проблеми. Таким чином, студент, виконуючи завдання викладача перед лекцією, вже знає певний матеріал і має власні думки щодо окреслених викладачем проблем. Очевидно, що в такій ситуації виникає підвищена мотивація до навчання: студенту цікаво, яке розвязання проблем, виявлених на лекції, висуне викладач і як воно співвіднесеться з його власним. Студент і викладач на таких лекціях виступають як рівні колеги; в основі спілкування лежить діалог в його внутрішньому прояві, що підвищує ефективність навчання на лекції.

Загальним для всіх типів лекцій є їх професійна спрямованість. У процесі викладання моделюється не лише зміст, але й враховуються педагогічні умови, які на нього впливають: специфічна форма фундаментальної підготовки майбутніх учителів математики, особистість самого викладача, власна позиція його щодо питань фундаментальної підготовки, вміння пояснити існуючі суперечності визначеної проблеми, показати розв’язання деяких суперечностей науковими розробками зарубіжних і українських науковців, що допомагає майбутнім педагогам визначити свою позицію стосовно фундаментальної підготовки.

Важливою формою фундаментальної підготовки у вищому навчальному закладі є науково-дослідна робота. Обов’язковими видами цієї роботи є написання курсових, а також, за бажанням, дипломних робіт. У розробці тематики визначених видів робіт ми дотримувалися системного підходу, який передбачає наскрізне дослідження теми. Також враховували, що обсяг тематики курсових робіт повинен узгоджуватися з тематикою дипломних робіт. Особливістю написання курсових робіт на фізико-математичному факультеті є, по-перше, те, що мета їх написання – розкрити питання, які не ввійшли до навчальної програми або на які відведено мало годин (наприклад, функціональні рівняння); по-друге, пояснення матеріалу за допомогою іншого розділу певного навчального предмета (довести подане твердження, спираючись на апарат аналітичної, проективної та диференціальної геометрії) або іншої навчальної дисципліни (фізики, інформатики тощо); по-третє, обов’язкове застосування цієї теорії в процесі роз’язання задач. Тематика дипломних робіт дає можливість студентам глибше відстежити певні аспекти досліджуваної проблеми.

Наприклад, на четвертому курсі запропонувано тему курсової роботи Методика обґрунтування методу внутрішнього проектування в позиційній геометрії. За умов впровадження науково-методичного супроводу тема дипломної роботи студента пятого курсу може бути сформульована так: Психолого-педагогічні основи навчання методу внутрішнього проектування в курсі стереометрії загальноосвітньої школи.

Науково-дослідна робота реалізується і в таких формах, як робота в проблемних групах, участь в олімпіадах, науково-практичних конференціях тощо. Їх основне завдання – формування прикладних умінь, розвиток потреби в творчій діяльності, професійній самоосвіті, оволодінні навичками науково-дослідної роботи.

Організація вивчення проективної геометрії передбачає застосування такої форми організації навчання, як практичні заняття, на яких здійснюється перенесення теоретичних знань у практичну діяльність з метою забезпечення більш глибокого їх засвоєння й оволодіння вміннями розвязувати задачі [4, с. 28].

Нестандартність організації практичних занять за розробленою технологією полягає у використанні в ході їх проведення таких трьох групових форм: індивідуально-групової, єдиної групової та диференційовано-групової. Колективна праця активізує розумову діяльність студентів, підвищує відповідальність перед товаришами за виконання завдань, виховує такі якості, як взаємодопомога і взаємоконтроль, сприяє кращому засвоєнню навчального матеріалу.

Дамо характеристику кожної із зазначених форм.

Мета організації індивідуально-групової (ІГ) форми навчання полягає в тому, щоб кожен студент засвоїв знання не стільки самостійно, скільки внаслідок спілкування з товаришами та організації дискусій, які часто виникають під час обговорення розв’язків. У результаті запам’ятовування відбувається мимовільно, що забезпечує міцні й глибокі знання. Крім того, така форма роботи виховує в майбутніх учителів взаємну відповідальність, почуття колективізму, задовольняє природну потребу молоді в спілкуванні, розвиває їх організаторські й педагогічні здібності. Організацію ІГ форми навчальної діяльності можна проілюструвати на прикладі виконання індивідуальних завдань з проективної геометрії. Для використання цієї форми навчання поділяємо студентів навчальної групи на мікрогрупи (так звані групи-зірочки) згідно з математичними здібностями та педагогічними схильностями (див. додаток Л).

Метою використання єдиної групової (ЄГ) форми навчальної діяльності є економія часу на виконання всього завдання, можливість для викладача збільшити кількість завдань на занятті й розподілити роботу в групі-зірочці таким чином, щоб кожний її член повністю охопив усі етапи. Організація ЄГ форми відбувається таким чином: усі групи-зірочки отримують однакове завдання, наприклад: Дано дві паралельні прямі. На одній із них задано відрізок. Лише за допомогою лінійки поділити відрізок на пять рівних частин. Якщо попередньо зі всією академічною групою цю задачу розв’язати фронтально і студенти обізнані зі всіма етапами побудови, можна організувати групову форму роботи для виконання поставленого завдання. У такому разі всі студенти виписують проміжні етапи виконання завдання, а саме додаткові задачі, які потрібно розвязати: 1) на одній з двох паралельних прямих дано відрізок; за допомогою лінійки поділити його навпіл; 2) на прямій дано відрізок із серединою; тільки лінійкою через точку поза прямою провести пряму, паралельну до заданої; 3) за допомогою лінійки через точку, що не належить двом паралельним прямим, провести пряму, яка паралельна до заданих; 4) на одній із двох паралельних прямих дано відрізок; лише за допомогою лінійки збільшити даний відрізок удвічі; 5) на одній із двох паралельних прямих дано відрізок; лише за допомогою лінійки збільшити даний відрізок у пять раз; 6) на одній із двох паралельних прямих задано відрізок; лише за допомогою лінійки поділити відрізок на пять рівних частин. Потім старший групи або викладач призначає етапи виконання завдання відповідно до індивідуальних особливостей студентів. Наслідки побудов, проведених в інших групах-зірочках, обговорюються зі всіма студентами фронтально.

Мета використання диференційовано-групової (ДГ) форми організації навчальної діяльності – підвищити активність студентів на занятті, знаходити раціональні шляхи розв’язання, точність побудови, прищеплювати навички колективної науково-дослідної роботи. Студенти різних груп одержують різні завдання. Наприклад, на заняттях з проективної геометрії під час вивчення теми Ряди ІІ-го порядку одні групи-зірочки проводять побудову точок та дотичних за означенням рядів ІІ-го порядку через проективну відповідність, інші – за теоремою Паскаля чи Бріаншона. Члени груп-зірочок виконують побудову самостійно, потім результати зіставляють. У такому разі часто трапляється, що між групами виникають дискусії щодо раціональності побудови залежно від обраного методу.

Таким чином, групові форми навчальної діяльності сприяють створенню довірливих стосунків на заняттях, виховують відповідальність не тільки за себе, а й за товаришів, допомагають викладачам здійснювати індивідуальний підхід до кожного студента і контролювати його роботу опосередковано – через старшого чи інших членів групи-зірочки. Крім того вони сприяють оптимізації навчального процесу внаслідок підвищення складності пропонованих для роботи студентів завдань. Дискусії, що виникають у ході групової праці, сприяють мимовільному запам’ятовуванню матеріалу, що вивчається.

Формування мінігруп проводиться на основі вивчення математичних здібностей і педагогічних схильностей студентів.

Під математичними здібностями ми розуміємо рівень знань, якість умінь і навичок, здатність застосовувати їх у розв’язанні математичних задач. Виділяємо три рівні математичних здібностей студентів.

І рівень характеризується високим ступенем абстрагування, раціональності, варіативності мислення, глибокими знаннями і вільною орієнтацією в матеріалі, здатністю до просторової уяви, розв’язання творчих завдань (сильні студенти).

ІІ рівень визначається вмінням застосовувати знання у розв’язанні пошуково-дослідницьких задач, які потребують узагальнення, виділення головного, раціонального мислення (середні студенти).

ІІІ рівень характеризується знаннями репродуктивно-відтворювального плану (слабкі студенти).

Педагогічні схильності майбутнього вчителя – це наявність у нього:

· педагогічної спрямованості, тобто усвідомлення суспільної значущості педагогічної праці, потреби в спілкуванні й роботі з дітьми;

· педагогічних здібностей, під якими треба розуміти комплекс проектувальних, гностичних і організаторських умінь, що базуються на високій усвідомленості та вимогливості до себе і до інших [24].

Ми виділяємо три рівні педагогічних схильностей у студентів:

1-й (високий) характеризується наявністю педагогічної спрямованості й цілого комплексу педагогічних здібностей;

2-й (середній) – наявністю педагогічної спрямованості при відсутності окремих компонентів педагогічних здібностей;

3-й (низький) – слабкою педагогічною спрямованістю, наявністю лише деяких компонентів педагогічних здібностей, а також недостатньою вимогливістю до себе і до інших.

Залежно від рівня математичних здібностей і педагогічних схильностей ми виділили п’ять типів студентів – майбутніх учителів математики (див. табл. 5).

Таблиця 5

Типи студентів	Рівні математичних здібностей	Рівні педагогічних схильностей
1-й	І	1-й
2-й	І	2-й або 3-й
3-й	ІІ	1-й або 2-й
4-й	ІІ	3-й
5-й	ІІІ	1-й або 2-й

Аналіз складу студентських груп показав, що основна маса студентів належить до 2-4-го типів (70-80 %), значно менше (в межах 10-20 %) – до 5-го типу і дуже мало студентів 1-го типу (близько 8 %). На основі проведеної типізації ми розподілили всіх студентів на гетерогенні групи, що складалися з п’яти осіб (зірочка), до яких входили студенти різних типів. Під час формування цих груп враховано побажання самих студентів (для створення в групах взаєморозуміння й доброзичливої робочої атмосфери), а також рівномірний розподіл по групах студентів 1-2-го і 5-го типів. У групу-зірочку найчастіше входили один-два студенти 1-2-го типів, два-три – 3-4-го типів і один-два – 5-го типу; старшим обирали студента 1-го або 2-го типу, який ставав помічником викладача, головним консультантом та організатором роботи в групі.

Спілкування між студентами в групі-зірочці розвиває в них такі педагогічні вміння, як гностичні (знаходити й усувати помилки) та проектувальні (аналізувати хід розв’язання завдання, під час дискусії доводити правильність свого погляду, пояснювати якесь питання доступно й аргументовано). Опитування членів експериментальних груп показало, що студенти всіх п’яти типів у ході групової форми навчальної діяльності поглиблюють свої знання й набувають необхідні для вчителя математики професійні вміння й навички.

Забезпечення якості фундаментальної підготовки обумовлено використанням спеціально підібраної системи методів навчання , які являють собою способи послідовної взаємодії тих, хто навчається, й тих, хто навчає, що направлені на організацію засвоєння змісту навчання. Ознаки довільного методу: спрямованість на засвоєння певного елементу змісту освіти в його певному перевтіленні та організований педагогом характер навчально-пізнавальної діяльності студентів, що залежить від способу засвоєння цього змістового елементу. Методи повинні бути спрямовані на збагачення уяви, мислення, пам’яті, мовлення, розкриття суб’єктивного досвіду кожного. Організація експериментальної роботи передбачає використання як традиційних, так і нетрадиційних методів, які б дозволили сформувати в майбутніх педагогів готовність до виконання своїх професійних функцій. Вибір методів навчання за розробленою програмою спрямовано на досягнення якісного рівня знань. Одна з основних вимог до вибору методу – його активна і творча спрямованість.

Як багатомірне утворення, методи різносторонні, тому їх можна групувати чи класифікувати. В наш час відомі десятки їх класифікацій за різними ознаками [37, c. 76]: за джерелом передачі інформації (С.І. Перовський, Е.Я. Голант), за призначенням (М.А. Данилов, Б.П. Йосипов), за типом пізнавальної діяльності (І.Я. Лернер, М.М. Скаткін), за дидактичною метою (Г.І. Щукіна, І.Т. Огородников та інші), на основі поєднання методів викладання й методів навчання (М.І. Махмутов), за цілісним діяльнісним підходом (Ю.К. Бабанський) тощо.

Для якісної фундаментальної підготовки майбутніх учителів математики головним є не стільки міцне засвоєння студентами знань, умінь та навичок, скільки становлення творчого потенціалу особистості фахівця. Виходячи з цього, методи навчання умовно поділимо за рівнем прояву творчого потенціалу на дві групи: 1) репродуктивні; 2) продуктивні.

Репродуктивні методи поділяються на дві групи: інформаційно-рецептивні та інструктивно-репродуктивні.

Мета викладача, який застосовує інформаційно-рецептивні методи , – формування певного кола уявлень про проективну геометрію, при цьому його діяльність полягає в організації сприйняття готової інформації, згідно з принципами доступності, наочності, систематичності та послідовності. Засоби, необхідні для цієї діяльності, містять креслення, схеми, підручники тощо.

Мета студента – первісне засвоєння знань; його діяльність складається зі сприйняття, усвідомлення й запам’ятовування сприйнятого. Засобами виступають лекційні записи, опорні конспекти, підручники тощо.

Результатом навчання в процесі використання інформаційно-рецептивних методів є сформованість у студента кола знань і уявлень, які дозволяють орієнтуватися в подальшій діяльності.

До інформаційно-рецептивних методів належать такі:

- пояснювально-ілюстративний виклад (пояснювально-ілюстративна лекція) – вихідне положення цього методу – констатація матеріалу теоретичного характеру, який поєднується з прийомами активізації пізнавальної діяльності студентів (виписуванням основної думки, конспектуванням, складанням схем тощо);

- образно-асоціативний виклад (лекція-візуалізація) – це усний монолог викладача, який подає студентам образно-асоціативну конструкцію (опору) навчального матеріалу, що сприяє запамятовуванню інформації й усуненню перевантажень у навчанні (наприклад, пояснення проективної та перспективної відповідності за допомогою значків тощо);

- ілюстративний метод (креслення, схеми) поєднується з вербальними (словесними) методами навчання;

- пояснення з повтором – використовують на лекціях при вивченні теоретичного матеріалу, доведенні теорем, розв’язанні задач на практичних заняттях.

Наприклад, при поясненні важких питань на лекціях з математики пропонуємо таку схему: спочатку викладач пояснює матеріал, а студенти слухають, але не записують; потім лектор відповідає на запитання й пропонує студентам записати матеріал в зошити. Як правило, нотатки вдається зробити лише декільком, оскільки більша частина аудиторії до цього моменту досягла лише попереднього розуміння, що не піддається словесному викладу. Тоді лектор повторює пояснення – на цей раз при підвищеній увазі аудиторії, оскільки матеріал набуває особистісної зацікавленості для кожного слухача. Завершальний етап схеми – студенти записують матеріал у зошит (записування можливе під диктування). Такий прийом проведення лекції більш сприйнятливий для підвищення пізнавальної активності студентів. Оскільки саме на лекціях з фундаментальних дисциплін пояснювальний матеріал відіграє більш вагому роль, ніж розповідний.

У межах інструктивно-репродуктивних методів мета викладача – формувати в студентів уміння та навички, спрямовувати їх на способи діяльності репродуктивного характеру. Діяльність викладача зводиться до інструктажу студента про способи будь-якої діяльності. Засобами виступають письмові вказівки, алгоритми, приклади дій.

Мета студента – вміти виконувати певний вид діяльності, попередньо оволодівши певними діями та операціями. Пізнавальна діяльність студента зводиться до виконання зразків дій, операцій певного виду. В результаті такий досвід стає вміннями та навичками. Засобами тут виступають завдання репродуктивного рівня.

Зміни особистості полягають у її готовності до діяльності. Результатом навчання студента є оволодіння різними способами діяльності, що дозволяють їх відтворення.

До інструктивно-репродуктивних методів належать:

- інструктаж (правила, алгоритми тощо) реалізується з метою розяснення студентам призначення певних дій, способів їх здійснення, умов розвязання практичних задач, послідовності операцій, які входять до того чи іншого вміння, характеристики типових ситуацій та їх використання, застосування на практиці тощо;

- складання плану лекції – попередній запис плану лекції на дошці під час перерви чи в зошиті до читання лекції відіграє мотивуючу, організовуючу й орієнтуючу роль, хоча менше активізує самостійність розумової діяльності студентів;

- самостійне конспектування – цей метод використовуємо для осмислення й засвоєння нового матеріалу студентами.

Студенти можуть виконувати такі види завдань: записати самостійне доведення теореми за аналогією до проведеного раніше викладачем; зробити виписки довідок, повідомлень з посібників, статей, які доповнюють матеріал лекції, заповнити таблиці; привести еквівалентні визначення понять і підходи до розгляду якоїсь проблеми, що відрізняються від записаних на лекції. Але спочатку має бути проведений інструктаж і здійснена перевірка виконання завдань на практичних та індивідуальних заняттях. Наприклад, на лекціях з аналітичної геометрії, розглядаючи конічні перерізи, можна повністю дослідити еліпс і записати його властивості, а дослідження гіперболи й параболи записати самостійно.

- домашня робота з літературою є логічним продовженням опрацювання теоретичного матеріалу, розглянутого на лекції.

Її можна проводити таким чином: слухачам ставлять запитання й пропонують знайти розв’язання. Не даючи відповіді на поставлене запитання, називають список літератури, де неважко знайти відповідь (список літератури із вказівкою на сторінки й абзаци має бути невеликим (дві-чотири назви) й бібліографічно правильно оформлений).

Завдання з проективної геометрії для самостійного опрацювання

За малим принципом двоїстості дати означення повному чотиристороннику і сформулювати його гармонічні властивості.

- завдання репродуктивного рівня включають у себе теоретичні питання або декілька однокрокових задач, відповіді на які мають показати підготовку студентів до заняття і є необхідною базою їх подальшої успішної роботи. До таких завдань належать і багатокрокові задачі з алгоритмом розвязання.

При використанні продуктивних методів змінюються цілі викладача й студента.

Педагог ставить собі за мету активно формувати пізнавальні здібності, професійні інтереси й світогляд, досвід творчої діяльності. Оскільки останнє засвоюється лише при розвязанні проблемних завдань, то діяльність викладача полягає ще і в організації проблемних ситуацій, під якими ми розуміємо психічний стан студента, що складається з трьох позицій: усвідомлення протиріч, сприйняття їх як труднощів і бажання їх розвязати. Засобами, які допомагають викладачу ефективно організувати цей метод навчання, є задачі середнього й вищого рівня складності, додаткова література, що відображає ряд точок зору на одне й те саме питання, яке має в науці парадокси, звернені до реального життя та співвіднесені з науковими фактами.

Мета студента – активне творче пізнання, механізм якого відповідає науковому дослідженню (проблема, гіпотеза, доведення, висновки). Засоби для студента в цьому випадку частково або повністю збігаються із засобами для викладача.

Досвід творчої діяльності, засвоєний особистістю, готує її до участі в творчому перетворенні культури. Саме в цьому полягають якісні зміни особистості. Результатом навчання тут виступає наявність у студентів структур творчого мислення.

- проблемний виклад (лекція проблемного характеру) – усний монолог викладача, який активізує продуктивну діяльність шляхом створення у студентів проблемної ситуації з наступною пропозицією щодо її розвязання, що потребує аргументації та доведення;

- дослідницький метод (практичні й теоретичні завдання середнього та вищого рівня складності) – завдання такого рівня використовуються для усунення такого недоліку в навчанні, на який звертав увагу М.М. Скаткін [31], – відсутність роботи із сильними студентами та розвиток творчого мислення в усіх студентів, а також їх самокритичності щодо своїх знань. Такі завдання дають змогу викладачеві індивідуалізувати роботу студентів з різними математичними здібностями;

- метод проектів – це творча самостійна робота для створення за допомогою програми PowerPoint мультимедійної презентації прикладів розв’язування задач.

Студент вибирає з переліку задачу з свого варіанту (див. додаток M). Оформлення задачі має містити, крім ходу розв’язання, також викладки теоретичного матеріалу.

Проект розрахований на чотири тижні, має свої критерії оцінювання. За більш детальною інформацією можна звертатися на студентський сайт, там також розміщений приклад студентської презентації.

Як бачимо, різні методи виконують різні функції: для репродуктивних домінуючою є навчаюча фунція, для продуктивних – розвиваюча.

Застосування вказаної групи методів неможливе без системи перевірки знань і вмінь. Механізм контролю в навчальному процесі відіграє значну роль у пізнавальній діяльності студентів:

· у процесі перевірки студенти повторюють і закріплюють вивчений матеріал (навчаюча функція);

· надходить інформація про помилки та недоліки в знаннях, уміннях, навичках студентів при оволодінні навчальним матеріалом, яка допомагає вибрати найбільш інтенсивну методику навчання (діагностична функція);

· надходить для викладача інформація про засвоєння наступної порції навчального матеріалу (розділу, теми) (прогностична функція);

· стимулюється пізнавальна активність студентів, розвиваються їх творчі здібності (розвивальна функція);

· надходить інформація про ступінь засвоєності та глибини навчального матеріалу (орієнтуюча функція);

· виховується у студентів відповідальне ставлення до дисципліни, навчання, охайність, чесність (виховна функція).

Важливим кроком на шляху реформуваня національної освіти є впровадження кредитно-модульної системи організації навчання, яка передбачає реорганізацію традиційної системи контролю й оцінки навчальних досягнень студентів у рейтинговову .

Рейтинг – це певна числова величина, яка виражається, як правило, за багатобальною шкалою, комплексний показник якості знань студента порівняно з успіхами його товаришів з одного чи декількох предметів протягом певного періоду навчання (модуль, семестр, рік тощо) [1, с. 11-12]. Сума оцінок, накопичених за певний період навчання, є кількісним показником якості роботи студента. Він повинен знати заздалегідь, яку максимальну та мінімальну кількість балів він може одержати за конкретно виконану роботу в результаті успішної діяльності. Необхідно вказувати умови, за яких студент зможе набрати найбільшу кількість балів і які дадуть можливість автоматичного виставлення заліку, складання семестрового іспиту тощо. За різні форми контролю студент має отримувати неоднакову кількість балів, відповідно до складності завдання.

На відміну від традиційної оцінки, рейтингова є сумою оцінок окремих видів робіт: лабораторних, практичних, колоквіумів тощо. Основними формами контролю, які застосовуються при рейтинговому оцінюванні успішності студентів, є тестові завдання, самостійні й контрольні роботи, індивідуальні завдання тощо. Головними вимогами застосування рейтингу є: готовність викладачів та студентів, методичне забезпечення, самостійна робота студентів, здійснення відповідної підготовчої роботи.

Впровадження рейтингового оцінювання успішності студентів вищих навчальних закладів формує більш відповідальне ставлення до навчання, підвищує об’єктивність в оцінці, посилює мотиваційний компонент, зменшує психологічне навантаження під час іспиту, запроваджує здорову конкуренцію, формує самостійність дій та перетворює контроль у дієву складову управлінського процесу.

Використання рейтингової системи має цілу низку відчутних переваг як для студентів, так і викладачів, а також для організації самого навчального процесу.

Для організації навчального процесу:

· відчутно впливає на його характер і є фактично його новою технологією;

· усуває упереджений підхід до оцінки знань, істотно розширює шкалу оцінок (міряємо, образно кажучи, не метрами, а сантиметрами), що дає можливість об’єктивніше порівнювати успіхи студентів;

· зумовлює нові фактори заохочення до праці, підвищує роль змагання чи навіть конкуренції, а також відповідальність студента за результати навчання, що дуже важливо для утвердження культу навчання;

· розширює рамки і значення самостійної роботи студентів;

· знімає штурмівщину і проблеми відвідування занять;

· дає можливість продовжити семестр шляхом скорочення заліково-екзаменаційної сесії;

· дозволяє успішно впроваджувати в навчальний процес гнучкі навчальні плани, різноманітні форми індивідуального навчання;

· сприяє підвищенню якості навчання, а відтак – рівня підготовки конкурентноспроможних фахівців;

· змінює взаємостосунки викладачів і студентів у напрямі утвердження сучасної педагогіки співпраці.

Для викладача:

· дає змогу реалізувати його прагнення до диференційованого, індивідуального підходу в роботі зі студентами;

· сприяє більш активно, творчо, методично обґрунтовано вести викладання дисциплін;

· підвищує точність та об’єктивність оцінки успішності навчання;

· дозволяє бути не озвучувачем (рупором) інформації з дисципліни, а помічником студентів у здобутті знань.

Для студента:

· орієнтує його на всебічне розкриття своїх здібностей;

· активізує його роботу, робить її ритмічною і систематичною протягом усього періоду навчання;

· вносить більше вмотивованості в його дії;

· формує самостійність, ініціативність, творчість і відповідальність;

· сприяє підвищенню якості знань завдяки систематичній роботі;

· стимулює загальну активність завдяки елементу змагання;

· підвищує об’єктивність оцінювання його знань, майже повністю виключає випадкову залежність від вдалої (невдалої) відповіді на заліку чи екзамені;

· допомагає уникнути психологічних, емоційних і фізичних перевантажень у ході заліково-екзаменаційних сесій;

· спонукає до дотримання навчальної дисципліни;

· ранжирує студентів у групі за рівнем знань.

Розглянемо на прикладі вивчення проективної геометрії введення рейтингової системи в навчальний процес.

Види оцінювання знань, умінь і навичок (приклад):

1. Активність студента на практичному занятті (завдання І-го та ІІ-го рівнів – по 1 б., завдання ІІІ-го рівня – по 2 б.).

2. Домашня робота студента (по 2 б. за опрацювання теоретичного матеріалу й за розв’язані задачі).

3. Тестування – 4 б.

4. Проект – 10б.

5. Контрольна робота – 20 б.

6. Відвідування лекційних занять по 1 б.

7. Ведення конспекту – 2 б.

Активність студента на практичному заняття та виконання домашньої роботи полягає в самостійному розвязуванні задач та опрацюванні теорії. Результат можна заносити у відповідні облікові відомості студентів на кожне практичне заняття (табл. 6).

Таблиця 6

Облікова відомість студентів

Практичне заняття № … Тема: ……..

№ з\п

Прізвище студента

Активність студента

Перевірка домашнього завдання

Усього

І рівень

ІІ рівень

ІІІ рівень

Теоретична частина

Задачі

1

2

3

30

Мета тестування – швидка перевірка знань обовязкового матеріалу (означення, теореми). Тестування є лише частиною контролю. Тести складено з нескладних завдань, які перевіряють засвоєння матеріалу на обовязковому рівні (тут не перевіряються вміння доводити теореми, розвязувати задачі). Врахування часу на проведення тесту допомагає студентові зосередитися саме на відповідях, виключає можливість користуватися додатковим матеріалом, а також консультуватися з товаришами. Тестування проводиться після повного лекційного курсу, в кінці семестру.

На контрольну роботу відводиться 2 години. Завдання індивідуальні для кожного студента й містять пять задач різного рівня складності: одна першого рівня (оцінюється в 2 бал), по дві другого й третього (оцінюються відповідно по 4 та 5 балів).

Оцінювання ведення конспекту передбачає виставлення балів за такими критеріями:

1) наявність усіх лекцій;

2) наявність формулювань основних означень, лем, теорем;

3) наявність пояснень теоретичного плану, доведень теорем;

4) якість малюнків;

5) наявність доопрацьованого, не розкритого на лекції матеріалу.

Далі всі бали сумуються й виставляються в загальну облікову відомість (табл. 7).

Таблиця 7

Загальна облікова відомість студентів

№ з\п	Прізвище студента	Практичні заняття ()	Тестування	Проект	Контрольна робота	Відвідування лекцій ()	Ведення конспекту	Усього балів
1
2
30

Максимально можна набрати за роботу протягом семестру 50 балів.

На екзамен виділяється теж 50 балів. Отже, максимальна сума дорівнює 100 балам. Оцінка виставляється згідно з прийнятим в університеті Положенням про рейтингову оцінку.

Отже, рейтингова система оцінки знань не тільки можлива, а й бажана в сучасному вищому навчальному закладі, оскільки забезпечує комплексний підхід до оцінювання знань, дає змогу врахувати обсяг, якість засвоєного матеріалу, стимулює самостійну роботу студентів, активізує їх пізнавальну діяльність, допомагає аналізувати навчальний процес у динаміці. Вона позитивно впливає на організацію навчального процесу загалом, а в кінцевому результаті – на якість підготовки спеціалістів.

Технологічна постановка цілей обумовлює на початковому етапі чітке окреслення результатів фундаментальної підготовки.

Як відомо, результат – це матеріальний або нематеріальний продукт діяльності, що очікується.

Розглядаючи розроблену технологію забезпечення якості фундаментальної підготовки майбутніх учителів математики як інноваційну технологію, ми вслід за авторами видання Ситуаційна методика навчання [30] вважаємо, що підвищення якості фундаментальної підготовки майбутніх учителів математики шляхом партнерських стосунків у навчальному процесі між викладачем і студентом спрямоване не тільки і не стільки на одержання знань, але й на формування здатності до творчості, опрацювання великих масивів інформації, вмінь і навичок професійної практичної діяльності [30, с. 132].

У загальному вигляді результат реалізації технології забезпечення якості фундаментальної підготовки майбутніх учителів математики можна сформулювати в такому вигляді: знання, вміння й навички з можливим домінуванням кожної складової сукупного результату.

Отже, вищезазначене дає підстави представити розроблену технологію у вигляді моделі (див. рис. 3).

.

3. Технологія забезпечення якості фундаментальної підготовки майбутніх учителів математики

Список використаних джерел та літератури

1. Беспалько В.П. Программированное обучение: Дидактический аспект. – М., 1970. – С. 47-62.

2. Аузіна М.О., Голуб Г.Г., Возна А.М. Система комплексної діагностики знань студентів. Навчальний посібник. – Львів: Львівський банківський інститут НБУ, 2002. – 38 с.

3. Богословский В. Научное сопровождение образовательного процесса в педагогическом университете: методологические характеристики. – СПб., 2000. – 141 с.

4. Бондар В.І. Дидактика: Підручник. – К., 2005. – 191 с.

5. Великий тлумачний словник сучасної української мови / Укл. гол. ред. В. Бусел. – К.: Ірпінь: ВТФ Перун, 2001. – 1440 с.

6. Глинська М.Л. Шляхи вдосконалення роботи вчителя інформатики // Компютер у школі та сім’ї. – 1999. – № 4. – С. 12-14.

7. Дичківська І.М. Інноваційні педагогічні технології: Навч. посібник. – К.: Академвидав, 2004. – 352 с.

8. Жебровський Б.М., Ломаковська Г.В. Інформатизація навчального процесу столиці: крок у ХХІ ст. // Компютер у школі та сім’ї. – 1998. – № 3. – С. 3-6.

9. Концепція підготовки, перепідготовки та підвищення кваліфікації фахівців для галузі зв’язку та сфери інформатизації до 2007 року / Затверджено наказом Державного комітету зв’язку та інформатизації України № 19 від 03.02.2003 р. – Київ, 2003. – 12 с.

10. Кукушин В.С. Дидактика (теория обучения): Учебное пособие. – Москва: ИКЦ МарТ, Ростов-н/Д: Издательский центр МарТ, 2003. – 368 с.

11. Лісова Н.І. Розвиток психолого-педагогічної компетентності молодих учителів у системі післядипломної освіти: Автореферат дис. ...канд. пед. наук: 13.00.04. – К., 2005. – 20 с.

12. Лозова В.І., Троцко Г.В. Теоретичні основи виховання і навчання: Навч. посібник для студ. пед. навч. закладів / Харківський держ. педагогічний ун-т ім. Г.С.Сковороди. — 2. вид., випр. і доп. — Х.: ОВС, 2002. — 400 с.

13. Максимова В.Н. Акмеология: новое качество образования: Книга для педагога. – СПб.: Изд-во РГПУ им. А.И. Герцена, 2002. – 99 с.

14. Моніторінг якості навчання – необхідна умова становлення творчої особистості й розвитку освітньої інституції (за результатами діагностування навченості учнів у школах області) / М.М. Барна, Г.М. Мокрицька, Н.І. Новикова та ін., За ред. Р.Б. Шияна. – Л.: ЛОНМІО, 2000-2001. – 178 с.

15. Наукова школа: центр професійної підготовки педагогічних кадрів (науковий доробок викладачів та аспірантів кафедри педагогіки Житомирського державного педагогічного університету імені Івана Франка): Науковий збірник / За ред. проф. О.А. Дубасенюк – Житомир: Житомир. держ. пед. ун-т, 2003. – 334 с.

16. Науково-педагогічний пошук молодих дослідників: Збірник наукових праць студентів та аспірантів / За ред. О.А. Дубасенюк, А.В. Іванченка – Житомир: ЖДПУ, 2000. – С. 20-21.

17. Никитина Н.Н., Железнякова О.М., Петухов М.А. Основы профессионально-педагогической деятельности: Учеб. пособие для студ. учреждений сред. проф. образования. – М., 2002. – 288 с.

18. Онищук Л.А. Інноватика – істотна складова гуманістичної парадигми учіння // Шлях освіти. – 2000. – № 4. – С. 13-16.

19. Основні завдання АПН на виконання рішень ІІ Всеукраїнського з’їзду працівників освіти та Указу Президента України Про додаткові заходи щодо забезпечення розвитку освіти в Україні. Доповідь Президента АПН України В. Кременя. – Педагогічна газета. – 2001. – № 12 (41). – С. 23-31.

20. Основы педагогики высшей школы: Уч. пособие / Составители: Р.И. Хмелюк, И.М. Богданова, Н.И. Дидусь, З.Н. Курлянд, М.Ф. Ломонова, Н.А. Шевченко, О.М. Яций. – Одесса: ЮГПУ им. К.Д. Ушинского, 1998. – 96 с.

21. Пидкасистый П.И., Тыщенко О.Б. Компьютерные технологии в системе дистанционного обучения // Педагогика. М., – 2000. – № 5. – С. 7-13.

22. Підласий І.П. Діагностика та експертиза педагогічних проектів: Навч. посібник / Міжнародний фонд Відродження. — К. : Україна, 1998. — 343 с.

23. Положення про організацію навчального процесу у вищих навчальних закладах, МОН 02.06.1993 р. № 161.

24. Про Національну доктрину розвитку освіти: Указ Президента України // Законодавчі акти України з питань освіти: Зб. – К.: Парламент. вид-во, 2004.

25. Програми для фізико-математичних факультетів педагогічних інститутів. Збірник № 1 // Рекомендовано комісією з математичних наук науково-методичної ради Міністерства освіти України. Протокол № 3 від 4.06.92. – К., 1993. – 176 с.

26. Резервы интенсификации учебно-воспитательного процесса педвуза: Межвуз. ст. науч. тр. – Кострома: КГПИ, 1990. – 136 с.

27. Ротаєнко П.А., Самойленко Н.І. Реалізація перевірки знань учнів у мультимедійних системах навчання // Компютер у школі та сім’ї. – 1998. – № 4 (8). – С. 15-18.

28. Сбруєва А.А. Тенденції реформування середньої освіти розвинених англомовних країн у контексті глобалізації (90-ті рр. ХХ – початок ХХІ ст.): Монографія. – Суми: ВАТ Сумська обласна друкарня. Видавництво Козацький вал, 2004. – 500 с.

29. Селевко Г.К. Современные образовательные технологии: Учеб. Пособие. – М.: Народное образование, 1998. – 256 с.

30. Ситуаційна методика навчання: теорія й практика / Упор. О. Сидо-ренко, В. Чуба. – К., 2001. – 256 с.

31. Скаткин М.Н. Проблемы современной дидактики. – М.: Педагогика, 1980. – 96 с.

32. Смульсон М.Л. Інтелектуальні навчаючі системи: теоретичний аспект // Компютер у школі та сім’ї. – 1998. – № 4. – С. 3-6.

33. Соловьева И.П. Научно-методическое сопровождение деятельности педагогического коллектива как условие реализации личностного подхода (на примере системы образования Таймырского округа): Автореферат дис. ...канд. пед. наук: 13.00.01. – СПб, 2005. – 18 с.

34. Сорочан Т.М. Підготовка керівників шкіл до управлінської діяльності: теорія та практика / Луганський національний педагогічний ун-т ім. Тараса Шевченка. — Луганськ : Знання, 2005. — 384 с.

35. Столяренко О.М. Формування гуманістичних рис школярів загальноосвітньої школи // Освіта і управління. – 1999. – № 3. – С. 53.

36. Сухомлинська О. Про стан теорії та практики виховання в освітньому просторі // Шлях освіти. – 1998. – № 3. – С. 5.

37. Теоретические основы непрерывного образования / Под ред. В. Онушкина. – М.: Педагогика, 1987. – 208 с.

38. Теоретические основы процесса обучения в современной школе / Под ред. В.В. Краевского, И.Я. Лернера. – М., 1989. – 287 с.

39. Терещенко Т.П. Структура експертної системи // Компютер у школі та сім’ї. – 1998. – № 3. – С. 31-36.

40. Холодная М.А. Формирование персонального познавательного стиля ученика как одно из направлений индивидуализации обучения // Теория и практика продуктивного обучения / Составитель: Башмаков М.И. – М.: Народное образование, 2000. – С. 21-25.

Скачать архив с текстом документа