Тема 10. Рекурсивные частотные цифровые фильтры благословен Господь, кто содеял все нужное нетрудным, а все трудное ненужным

СОДЕРЖАНИЕ: Рекурсивные фильтры нужны при обработке данных. Однако разрабатывать их трудно. Отсюда следует, что Всевышний фильтров не создавал, и за последствия их применения ответственности не несет

ЦИФРОВАЯ ОБРАБОТКА СИГНАЛОВ

Digital signals processing. Digital recursive frequency filters.

Тема 10. РЕКУРСИВНЫЕ ЧАСТОТНЫЕ ЦИФРОВЫЕ ФИЛЬТРЫ

Благословен Господь, кто содеял все нужное нетрудным, а все трудное ненужным.

Григорий Сковорода. Украинский философ, ХIII в.

Рекурсивные фильтры нужны при обработке данных. Однако разрабатывать их трудно. Отсюда следует, что Всевышний фильтров не создавал, и за последствия их применения ответственности не несет.

Отец Дионисий, в миру В.Лебедев. Геофизик Уральской школы, XX в.

Содержание

Введение.

1. Низкочастотный ф ильтр Баттеруорта. Передаточная функция. Крутизна среза. Порядок фильтра. Преобразование Лапласа. Билинейное преобразование.

2. Высокочастотный фильтр Баттеруорта. Синтез фильтров методом частотного преобразования.

3. Полосовой фильтр Баттеруорта. Расщепление спектра. Полосовой фильтр на s-плоскости. Передаточная функция.

4. Фильтры Чебышева. Фильтры первого рода. Фильтры второго рода.

5. Дополнительные сведения.

Введение

Процесс проектирования рекурсивного частотного фильтра обычно заключается в задании необходимой передаточной характеристики фильтра в частотной области и ее аппроксимации с определенной точностью какой-либо непрерывной передаточной функцией, с последующим z-преобразованием для перехода в z-область. Первые две операции хорошо отработаны в теории аналоговой фильтрации сигналов, что позволяет использовать для проектирования цифровых фильтров большой справочный материал по аналоговым фильтрам. Последняя операция является специфичной для цифровых фильтров.

Для алгебраического преобразования непрерывной передаточной функции в многочлен по z используется билинейное преобразование, известное в теории комплексных переменных под названием дробно-линейного преобразования.

10.1. Низкочастотный фильтр Баттеруорта /12,24/.

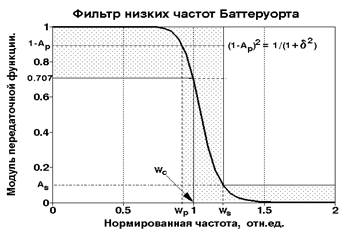
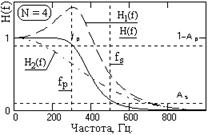
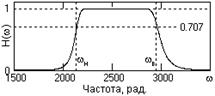
Рис. 10.1.1. АЧХ фильтра Баттеруорта.

Передаточная функция . Гладкий вид амплитудно-частотной характеристики фильтра Баттеруорта (рис. 10.1.1) задают квадратом передаточной функции вида:

|H(W)|² = H(W)H*(W) = 1/(1+W^2N ).

где W = w/w_c - нормированная частота, w_c - частота среза АЧХ фильтра, на которой |H(w)|² = 1/2 (соответственно H(w) = 0.707, или 3 дб), N - порядок фильтра, определяющий крутизну среза АЧХ. Функция |H(W)|² – представляет собой энергетический спектр сигнала (спектральную плотность мощности) и не имеет фазовой характеристики, т.е. является четной вещественной, образованной произведением двух комплексно сопряженных функций H(W) и H*(W), При W 0 коэффициент передачи фильтра стремится к 1. Учитывая, что результаты вычислений будут относиться к цифровым фильтрам и при z-преобразовании с переходом в главный частотный диапазон произойдет искажение частот, до начала расчетов фактические значения задаваемых частотных характеристик (значения w_c , w_p и w_s ) следует перевести в значения деформированных частот по выражению:

w_д = (2/Dt) tg(wDt/2), -p/Dtwp/Dt. (10.1.1)

Крутизна среза. Наклон частотной характеристики фильтра при переходе от области пропускания к области подавления можно характеризовать коэффициентом крутизны среза фильтра K в децибелах на октаву:

K = 20 log|H(w₂ )/H(w₁ )|, (10.1.2)

где w₁ и w₂ - частоты с интервалом в одну октаву, т.е. w₂ = 2w₁ .

Длительность импульсной реакции фильтра в пределах ее значимой части также зависит от крутизны среза: чем больше крутизна, тем больше длительность импульсного отклика фильтра.

Порядок фильтра. Принимая w₁ =W_c , w₂ =W_s и подставляя в (10.1.2) значения H(W) с приведенными данными, получим приближенное выражение для определения порядка фильтра по заданному значению К:

N = K/6. (10.1.6)

Так, для гарантированного ослабления сигнала в полосе подавления в 100 раз (40 децибел) порядок фильтра N = 7. В среднем, при изменении N на единицу коэффициент подавления сигнала изменяется на 6 децибел.

Исходные требования к передаточной функции фильтра обычно задаются в виде значений w_p , w_s и коэффициентов неравномерности (пульсаций) A_p и A_s (см. рис. 10.1.1). Для определения частоты среза w_c по уровню 0.707 и порядка фильтра введем параметр d, связанный с коэффициентом А_р следующим соотношением:

(1-А_р )² = 1/(1+d² ).

d = [1/(1-А_р )]= A_p /(1-A_p ). (10.1.3)

Для учета деформации частотной шкалы в процессе билинейного преобразования при переходе в дальнейшем к полиномам по Z, выполняем расчет деформированных частот w_dp и w_ds по формулам:

w_dp = 2 tg(w_p Dt/2)/Dt, (10.1.4)

w_ds = 2 tg(w_s Dt/2)/Dt.

При нормированной частоте W = w/w_dc , где w_dc соответственно также деформированная частота, на границах переходной зоны выполняются равенства:

1/(1+d² ) = 1/[1+(w_dp /w_dc )^2N ], (10.1.5)

A_s ² = 1/[1+(w_ds /w_dc )^2N ].

Отсюда:

d² = (w_dp /w_dc )^2N , 1/A_s ² - 1 = (w_ds /w_dc )^2N .

Решая эти два уравнения совместно, находим:

N = ln [d/] / ln(w_dp /w_ds ), (10.1.6)

w_dc = w_dp /d^1/N . (10.1.7)

Пример расчета фильтра низких частот Баттеруорта.

Рис. 10.1.2.

Начиная с этого параграфа, будем сопровождать рассмотрение теории последовательным расчетом фильтра низких частот с применением приводимых формул. Для расчета примем следующие исходные параметры фильтра:

- Шаг дискретизации данных Dt = 0.0005 сек. Частота Найквиста f_N = 1/2Dt = 1000 Гц, _N = 6.283·10³ рад.

- Граничная частота пропускания: f_p = 300 Гц, w_p = 1.885·10³ рад.

- Граничная частота подавления: f_s = 500 Гц, w_s = 3.142·10³ рад.

- Коэффициенты неравномерности: А_р = А_s = 0.1.

Расчет дополнительных параметров:

1. Значение d по формуле (10.1.3): d= 0.484.

2. Деформированные частоты по формуле (10.1.4): w_dp = 2.038·10³ рад. w_ds = 4·10³ рад.

3. Порядок фильтра по формуле (10.1.6): N = 4.483.

Для пояснения порядка расчетов при четном и нечетном порядке фильтра, принимаем N1=4, N2=5.

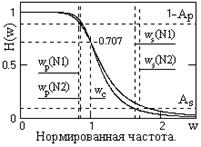
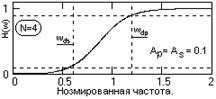
4. Частота среза по формуле (10.1.7): w_dc (N1) = 2.443·10³ рад (389 Гц), w_dc (N2) = 2.356·10³ рад (375 Гц).

5. По формуле H(w)= [1/(1+w^2N )]^1/2 , w = /_dc , строим графики передаточных функций (рис.10.1.2).

Преобразование Лапласа. Переводим функцию |H(W)|² на координатную ось пространства преобразования Лапласа при p = jW, для чего достаточно подставить W = p/j:

|H(р)|² = 1/[1+(p/j)^2N ]. (10.1.8)

Полюсы функции находятся в точках нулевых значений знаменателя:

1+(p/j)^2N = 0, p = j. (10.1.9)

Отсюда следует, что полюсы располагаются на единичной окружности в p-плоскости, а их местоположение определяется корнями уравнения (10.1.9). В полярных координатах:

p_n = j exp(jp(2n-1)/2N), n = 1,2, ... ,2N. (10.1.10)

p_n = j cos[p(2n-1)/2N] - sin[p(2k-1)/2N]. (10.1.10)

Рис. 10.1.2.

Продолжение примера.

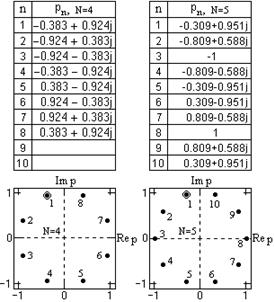
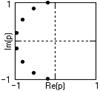
6. Вычисляем значения полюсов фильтра по формуле (10.1.10). Значения полюсов и их расположение на р-плоскости приведены на рис. 10.1.2. Положение первого полюса отмечено. Нумерация полюсов идет против часовой стрелки.

Как следует из формулы (10.1.10) и наглядно видно на рис. 10.1.2, все полюса с n N являются комплексно сопряженными с полюсами nN. Устойчивую минимально-фазовую передаточную функцию фильтра образуют полюса левой половины р-плоскости:

H(p) = G/B(p), (10.1.11)

где G - масштабный множитель, B(p) - полином Баттеруорта:

B(p) = B₁ (p) B₂ (p) ... B_N (p), (10.1.12)

B_n (p) = p-p_n . (10.1.13)

Практическая реализация фильтра Баттеруорта при четном значении N производится в виде последовательной каскадной схемы биквадратными блоками, т.е. составными фильтрами второго порядка. Для этого множители B(p) в (10.1.12) объединяются попарно с обоих концов ряда по n (от 1 до N) по комплексно сопряженным полюсам, при этом для каждой пары получаем вещественные квадратичные множители:

В_m (p) = B_n (p)·B_N+1-n (p) =

= [p+j exp(jp(2n-1)/2N)][p+j exp(jp(2(N+1)-2n-1)/2N)] =

= [p+j exp(jp(2n-1)/2N)][p-j exp(jp(2n-1)/2N)] =

= p² +2p sin(p(2m-1)/2N)+1, n = 1,2, ..., N/2; m = n. (10.1.14)

Общее количество секций фильтра M=N/2. При нечетном N к членам (10.1.14) добавляется один линейный множитель с вещественным полюсом p_(N+1)/2 = -1, пример положения которого на р-плоскости можно видеть на рисунке 10.1.2 для N=5:

В_(N+1)/2 (p)= p+1. (10.1.15)

Машинное время фильтрации на один оператор фильтра первого или второго порядка практически не отличаются, поэтому использование операторов первого порядка можно не рекомендовать и при установлении порядка фильтра по формуле (10.1.6) округлять расчетное значение N в сторону большего четного числа, что создает определенный запас по крутизне среза частотной характеристики.

Таким образом, передаточная функция ФНЧ Баттеруорта в p-области при четном N:

H(p) = G1/B_m (p) = G 1/(p² +a_m p+1), (10.1.16)

a_m = 2 sin(p(2m-1)/2N), m = 1,2, ... ,N/2. (10.1.17)

При нечетном N:

H(p) = (G/p+1)1/(p² +a_m p+1), (10.1.16)

Продолжение примера.

7. Вычисляем значения коэффициентов a_m по формуле (10.1.17):

- N=4: a₁ = 0.765, a₂ = 1.848.

- N=5: a₁ = 0.618, a₂ = 1.618.

Билинейное преобразование. Для перевода передаточной функции фильтра в z-область производится билинейное преобразование, для чего в выражение (10.1.16) подставляется параметр р:

p = g(1-z)/(1+z). (10.1.18)

С учетом автоматического возврата к нормальной шкале частот в главном частотном диапазоне z-преобразования значение коэффициента g:

g = 2/(Dt·_dc ). (10.1.19)

После перехода в z-область и приведения уравнения передаточной функции в типовую форму, для четного N получаем передаточную функцию из М=N/2 биквадратных блоков:

H(z) = GG_m (1+z)² /(1-b_m z+c_m z² ). (10.1.20)

G_m = 1/(g² + a_m g + 1). (10.1.21)

b_m = 2·G_m (g² - 1). (10.1.22)

c_m = G_m (g² - a_m g + 1). (10.1.23)

При нечетном N добавляется один линейный блок первого порядка, который можно считать нулевым блоком фильтра (m=0):

H(z) = GG_m (1+z)² /(1-b_m z+c_m z² ), (10.1.24)

при этом, естественно, в выражении (10.1.24) используются значения коэффициентов G_m , b_m и c_m , вычисленные по (10.1.21-10.1.23) для нечетного значения N.

Значение множителя G в общем случае находится нормировкой к 1 коэффициента передачи фильтра при w = 0. Для ФНЧ при использовании вышеприведенных формул значение G равно 1.

При z=exp(-jw) главный диапазон функций H(z) от -p до p. Для получения передаточной функции в шкале физических частот достаточно вместо z в выражения (10.1.20, 10.1.24) подставить значение z=exp(-jwDt), где Dt – физический интервал дискретизации данных, и проверить соответствие расчетной передаточной функции заданным условиям.

Рис. 10.1.3.

Продолжение примера.

8. Вычисляем значения коэффициентов G_m , b_m и c_m :

- N=4: g = 1.637, G₁ = 0.203, G₂ = 0.149, b₁ = 0.681, b₂ = 0.501, c₁ = 0.492, c₂ = 0.098.

- N=5: g = 1.698, G₁ = 0.203, G₂ = 0.151, b₁ = 0.763, b₂ = 0.568, c₁ = 0.574, c₂ = 0.171.

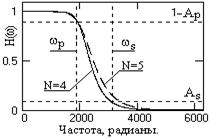
9. Подставляем вычисленные коэффициенты в выражения (10.1.20, 10.1.24) и вычисляем значения передаточных функций при z = exp(-jwDt). Графики полученных функций приведены на рис. 10.1.3. На рис. 10.1.4

Во временной области фильтрация выполняется последовательной сверткой входного сигнала с операторами ячеек фильтра:

y_k = x_k {h₀ (i)} h₁ (i) … h_М (i), i = 0,1,2.

Уравнение рекурсивной фильтрации для m-го оператора фильтра:

y_k = G_m (x_k +2x_k-1 +x_k-2 ) + b_m y_k-1 - c_m y_k-2 . (10.1.25)

Уравнение рекурсивной фильтрации для дополнительного h₀ (i) линейного оператора фильтра при нечетном N:

y₀ = (x_k +x_k-1 )/(g+1) + y_k-1 ·(g-1)/(g+1) (10.1.26)

Продолжение примера.

Рис. 10.1.4.

10. Каждый оператор фильтра имеет определенную передаточную функцию, что можно видеть на рис. 10.1.4. Порядок последовательной свертки сигнала с операторами фильтра значения не имеет, но с учетом разрядности ячеек памяти звено H₁ (f) целесообразно реализовать за H₂ (f).

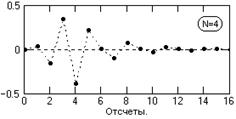
11. Для оценки длительности импульсной реакции фильтра подаем на вход фильтра импульс Кронекера на отсчете k = 3, и начинаем фильтрацию со второго отсчета (что обеспечивает начальные условия фильтрации на точках k=0 и k=1). Коэффициент усиления дисперсии шумов (сумма квадратов значений импульсного отклика) равен 0.341 при N=5, и 0.278 при N=4.

10.2. Высокочастотный фильтр Баттеруорта /12/.

Синтез фильтров методом частотного преобразования. Высокочастотные и полосовые фильтры конструируются путем частотной трансформации передаточных функций фильтров низких частот. Если обозначить аргумент передаточных функций ФНЧ через p=jW, a функций ФВЧ и ПФ через s=jw, то всегда можно найти такую функцию частотного преобразования p=F(s), которая превращает один тип фильтров в другой. Для преобразования ФНЧ ФВЧ функция частотного преобразования имеет вид:

p = 1/s, (10.2.1)

В этом нетрудно убедиться сравнением двух видов преобразования. Как известно, передаточная функция ФВЧ может быть получена из ФНЧ разностью между широкополосным фильтром (H(w)=1) и ФНЧ. Применяя этот метод для функции Баттеруорта, получаем:

|H(w)|² = 1-|H(W)|² = 1- 1/(1+W^2N ) = W^2N /(1+W^2N ). (10.2.2)

С другой стороны, при W = p/j: |H(p)|² = 1/(1-p^2N ). Выполняя подстановку (10.2.1) в это выражение, получаем:

|H(s)|² = s^2N /(s^2N -1).

Возвратимся из последнего выражения к аргументу w с учетом принятого равенства s=jw:

|H(s)|² = (jw)^2N /((jw)^2N -1) =(w)^2N /(1+(w)^2N ),

что полностью повторяет (10.2.2) при w=W.

Подставляя p=1/s непосредственно в выражение H(p) (10.1.16) для четного значения N, получаем:

H(s) = Gs² /(s² +a_m s+1). (10.2.3)

Для нечетного N:

H(s) = [G·s/(s+1)]s² /(s² +a_m s+1). (10.2.4)

После билинейного z-преобразования выражения с подстановкой s=g(1-z)/(1+z), для четного и нечетного значений N соответственно:

H(z) = Gg² ·G_m ·(1-z)² /(1-b_m z+c_m z² ). (10.2.5)

H(z) = Gg² ·G_m ·(1-z)² /(1-b_m z+c_m z² ). (10.2.6)

G_m = 1/(g² + a_m g + 1). (10.2.7)

b_m = 2·G_m (g² - 1).

c_m = G_m (g² - a_m g + 1).

Значения коэффициентов G_m , b_m , c_m остаются без изменения (сравнить с (10.1.21-10.1.23)). При задании частотных параметров ФВЧ в том же виде, что и для ФНЧ, формула расчетов N и w_dc получается аналогично ФНЧ, при этом в знаменателе выражения (10.1.6) отношение w_dp /w_ds заменяется на w_ds /w_dp :

N = ln [d/] / ln(w_ds /w_dp ), (10.2.8)

а в (10.1.7) деление членов правой части меняется на умножение:

w_dc = w_dp ·d^1/N . (10.2.9)

Уравнение рекурсивной фильтрации для m-го оператора фильтра:

y_k = g² ·G_m (x_k -2x_k-1 +x_k-2 ) + b_m y_k-1 - c_m y_k-2 . (10.2.10)

Уравнение рекурсивной фильтрации для дополнительного h₀ (i) линейного оператора фильтра при нечетном N:

y₀ = g·(x_k -x_k-1 )/(g+1) + y_k-1 ·(g-1)/(g+1). (10.2.11)

Пример расчета фильтра высоких частот Баттеруорта.

Техническое задание:

- Шаг дискретизации данных Dt = 0.0005 сек. Частота Найквиста f_N = 1/2Dt = 1000 Гц, _N = 6.283·10³ рад.

- Граничная частота полосы пропускания: f_p = 700 Гц, w_p = 4.398·10³ рад.

- Граничная частота полосы подавления: f_s = 500 Гц, w_s = 3.142·10³ рад.

- Коэффициенты неравномерности: А_р = А_s = 0.1.

Расчет дополнительных параметров:

1. d = A_p /(1-A_p ): d= 0.484.

2. Деформированные частоты по формуле (10.1.4): w_dp = 7.85·10³ рад. w_ds = 4·10³ рад.

3. Порядок фильтра по формуле (10.2.8): N = 4.483. Для расчетов принимаем N=4.

Рис. 10.2.1.

4. Частота среза фильтра по формуле (10.2.9):

w_dc = 6.549·10³ рад (1042 Гц),

5. Строим график функции H(w), w = /_dc , (рис.10.2.1).

6. Полюса p_n фильтра полностью повторяют полюса ФНЧ (рис. 10.1.2), а, соответственно, повторяются и значения коэффициентов a_m . Остальные коэффициенты: g = 0.611, G₁ = 0.543, G₂ = 0.4, b₁ = - 0.681, b₂ = - 0.501, c₁ = 0.492, c₂ = 0.098.

Рис. 10.2.2.

При сравнении коэффициентов b_m , c_m и коэффициентов в числителе передаточных функций ФВЧ с соответствующими коэффициентами ФНЧ предыдущего примера можно заметить, что в данном фильтре относительно ФНЧ произошла только смена знаков коэффициентов при нечетных степенях z. Это объясняется тем, что заданные в данном примере параметры ФВЧ по частоте соответствуют частотному реверсу ФНЧ: w = p-w, что приводит к частотному реверсу передаточной функции низкочастотного фильтра и превращению его в высокочастотный фильтр. Этот способ обращения ФНЧ также может использоваться для расчетов ФВЧ.

7. Импульсная реакция фильтра, вычисленная по (10.2.10) при подаче на вход фильтра импульса Кронекера приведена на рис. 10.2.2.

Курсовая работа 15-07. Разработка программы устранения сдвига фазы сигналов при использовании фильтров Баттеруорта.

10.3. Полосовой фильтр Баттеруорта /12/.

Как известно, полосовой фильтр можно получить непосредственной комбинацией низкочастотного и высокочастотного фильтра при перекрытии полосы пропускания фильтров. Аналогичный эффект достигается и частотным преобразованием ФНЧ, которое в этом случае имеет вид:

p = s+1/s. (10.3.1)

Подставив в (10.3.1) значения p = jW и s = jw, получим:

W = [w² -1]/w,

w² -Ww-1 = 0. (10.3.2)

Корни уравнения (10.3.2):

(w)_1,2 = W/2 . (10.3.3)

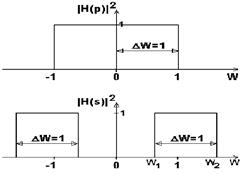
Расщепление спектра. При W=0 имеем w =1, т.е. центр полосы пропускания ФНЧ (от -W_c до +W_c ) расщепляется на два (как и положено, для полосовых фильтров) и смещается в точки w =1. Подставив в (10.3.3) граничную частоту W_с =1 нормированного ФНЧ, определяем граничные частоты нормированного полосового фильтра в виде пары сопряженных частот:

w₁ = 0.618, w₂ = 1.618

Рис. 10.3.1. Расщепление полосы.

Сущность произведенного преобразования наглядно видна на рис. 10.3.1. Ширина полосы пропускания нормированного ПФ равна 1.

Полученное преобразование можно распространить на полосовой фильтр с ненормированными частотами w_н и w_в .

Введем понятие геометрической средней частоты фильтра w_о :

w_о = . (10.3.4)

Ширина полосы пропускания ПФ связана (см. рис.10.3.1) с граничной частотой ФНЧ соотношением:

Dw = w_в -w_н = w_с = w_н .

В долях средней геометрической частоты:

W_н = (w_в -w_н )/w_о = W_c . (10.3.5)

Заменяя в (10.3.4-10.3.5) значение w_в на произвольную частоту w и подставляя в (10.3.5) значение _н = ·_о ² из (10.3.4), получаем произвольную частоту W:

W = (w-w_н )/w_о = w/w_o -w_o /w. (10.3.6)

Отсюда, в выражении (10.1.1) вместо нормированной частоты W = w/w_с можно применить функцию частоты полосового фильтра w(w):

w(w) = (w² -w_о ² )/[w(w_в -w_н )],

или, подставляя (10.3.4) вместо _о :

w(w) = (w² -w_н w_в )/[w(w_в -w_н )]. (10.3.7)

Тем самым передаточная функция ФНЧ выражается в единицах, которые позволяют после применения преобразования (10.3.1) использовать для задания необходимые граничные частоты w_н и w_в полосового фильтра.

Пример расчета полосового фильтра Баттеруорта.

Техническое задание:

- Шаг дискретизации данных Dt = 0.0005 сек. Частота Найквиста f_N = 1/2Dt = 1000 Гц, _N = 6.283·10³ рад.

- Нижняя граничная частота полосы пропускания: f_н = 340 Гц, w_н = 2.136·10³ рад.

- Верхняя граничная частота полосы пропускания: f_в = 470 Гц, w_в = 2.953·10³ рад.

- Крутизна срезов в децибелах на октаву: К_р = 45.

Расчет параметров:

Рис. 10.3.2.

1. Порядок фильтра по формуле (10.1.6): N = К_р /6 = 45/6 = 7.5.

Для расчетов принимаем N=8.

2. Строим график функции H(w) = с использованием выражения (10.3.7). Передаточная характеристика фильтра приведена на рис. 10.3.2.

3. Деформированные частоты по формуле (10.1.4):

w_dн = 2.366·10³ рад. w_dв = 3.64·10³ рад. w_do = 2.934·10³ .

Полосовой фильтр на s-плоскости. С учетом деформации частот, принимаем p = jw = j(w² -w_dн w_dв )/[w(w_dв -w_dн )], s= j и заменяем = s/j в выражении р:

р = (s² +w_{d н} w_{d в} )/[s(w_{d в} -w_{d н} )],

s² -p(w_{d в} -w_{d н} )s+w_{d н} w_{d в} = 0. (10.3.8)

Корни уравнения (10.3.8) определяют местоположение полюсов ПФ:

s = s* = p(w_dв -w_dн )/2 . (10.3.9)

Уравнение (10.3.9) показывает расщепление каждого p-полюса, определяемых выражением (10.1.14), на два комплексно сопряженных полюса s-плоскости, произведение которых будет давать вещественные биквадратные блоки в s-плоскости. При этом следует учесть то обстоятельство, что устойчивому рекурсивному фильтру на z-плоскости должны соответствовать полюса только одной (левой) половины p- и s - плоскостей.

Передаточная функция. При применении преобразования (10.3.1) к передаточной функции в полиномиальной форме (10.1.11), получаем:

H(p) = G1/(p-p_m ) - Gs/(s² -p_m s+1) = H(s), (10.3.10)

Выражение (10.3.10) не требует нахождения полюсов, т.к. они уже известны и определяются выражением (10.3.9). С учетом этого функция H(s) может быть записана с объединением в биквадратные блоки комплексно сопряженных полюсов с вещественными коэффициентами:

H(s) = Gs/[(s-s_m )(s-s*_m )] = Gs/(s² +a_m s+g_m ), (10.3.11)

где значения а_m и g_m могут быть определены непосредственно по полюсам (10.3.9):

a_m = -2 Re s_m , g_m = (Re s_m )² + (Im s_m )² = |s_m |² . (10.3.12)

Продолжение расчета.

Рис. 10.3.3. Рис. 10.3.4.

4. Полюса фильтра на единичной окружности в р-плоскости:

p_n = j·exp[j·p(2n-1)/2N], n = 1,2,…,N.

Положение полюсов приведено на рис. 10.3.3.

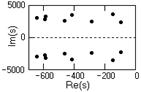
5. Полюса в левой половине s-плоскости, n = 1,2,…,2N

(приведены на рис. 10.3.4):

.

6. По полученным значениям полюсов вычисляем коэффициенты a_m и g_m (10.3.12), m = n.

a_m = 196.8, 300.4, 581.2, 834.5, 930.5, 1188, 1196, 1304.

g_m = 5.64·10⁶ , 1.314·10⁷ , 5.997·10⁶ , 1.236·10⁷ , 6.742·10⁶ , 1.1·10⁷ , 7.895·10⁶ , 9.39·10⁶ .

По приведенному примеру можно заметить, что при использовании ненормированных частот w, достаточно существенных по своей величине, значения s-полюсов и, соответственно, величины коэффициентов а_m и g_m имеют большие порядки, что нежелательно для дальнейших расчетов и может приводить к появлению погрешностей при ограничении разрядности. Для исключения этого фактора значения полюсов s_n рекомендуется нормировать на среднюю геометрическую частоту:

s_n = s_n /w_o .

Продолжение расчета.

6. Значения коэффициентов a_m и g_m (10.3.12), вычисленные по нормированным значениям s_n .

a_m = 0.067, 0.102, 0.198, 0.284, 0.317, 0.405, 0.407, 0.444.

g_m = 0.655, 1.527, 0.697, 1.436, 0.783, 1.277, 0.917, 1.091.

Коэффициент g билинейного преобразования для ненормированных значений w и полюсов s_n имеет классическую форму: g = 2/Dt. Соответственно, для нормированных значений: g = 2/(Dt·w_o ). После билинейного z-преобразования выражения (10.3.11), получаем:

H(z) = GG_m (1-z² )/(1-b_m z+c_m z² ). (10.3.13)

G_m = 1/(g+a_m +g_m g^-1 . (10.3.14)

b_m = 2G_m (g-g_m g^-1 ). (10.3.15)

c_m = G_m (g-a_m +g_m g^-1 . (10.3.16)

Продолжение расчета (по нормированным полюсам s_n ).

7. Значения коэффициента g: g = 1.363.

8. Значения G_m по (10.3.14): G_m = 0.523, 0.387, 0.483, 0.37, 0.444, 0.37, 0.409, 0.384.

9. Значения b_m по (10.3.15): b_m = 0.924, 0.188, 0.823, 0.23, 0.7, 0.315, 0.565, 0.432.

10. Значения c_m по (10.3.16): c_m = 0.93, 0.921, 0.809, 0.789, 0.719, 0.701, 0.666, 0.659.

11. Общий нормировочный множитель G: G = 1.264·10^-3 .

12. Заключительная передаточная функция:

При построении графика данной функции можно убедиться, что она полностью соответствует рис. 10.3.2.

13. Уравнение одной секции фильтра:

y_m,k = G_m ·(y_m-1,k - y_m-1,k-2 ) + b_m y_m,k-1 – c_m y_m,k-2 .

Нормировкой H(z) к 1 на геометрической средней частоте фильтра определяют общий множитель G:

G = 1/H(exp(-jDtw_o )). (10.3.17)

Если применить обратное частотное преобразование p = s(w_в -w_н )/(s² +w_в w_н ), то в результате будет получен полосовой заградительный фильтр.

Курсовая работа 16-07. Разработка программы расчета универсального частотного цифрового фильтра Баттеруорта (низкочастотный, высокочастотный, полосовой) и фильтрации цифровых сигналов .

10.4. Фильтры Чебышева /12/.

Фильтры первого рода. Фильтры Чебышева с пульсациями передаточной функции в полосе пропускания и гладким затуханием в полосе подавления называют фильтрами Чебышева первого рода, в отличие от инверсных фильтров Чебышева (второго рода). Аппроксимационная формула фильтров Чебышева первого рода определяется выражением:

|H(W)|² = 1/ [1+d_N ² T_N ² (W)], (10.4.1)

где Т_N (W) - многочлен Чебышева N-го порядка:

T_n (W) = cos(n arccos(W)), W1. (10.4.2)

= ch(n arcch(W)), W1. n = 1,2,...

Критерий приближения Чебышева , который широко используется не только в теории фильтров - минимум максимальной ошибки приближения (минимаксное приближение). В соответствии с этим приближением параметры передаточной функции подбираются таким образом, чтобы в полосе передачи АЧХ наблюдались равноволновые пульсации коэффициента передачи, которые являются платой за повышение крутизны среза фильтра.

Полиномы Чебышева вычисляются по рекуррентной формуле:

T_n (W) = 2W T_n-1 (W) - T_n-2 (W), (10.4.3)

T₁ (W) = W, T_o (W) = 1.

Для ФНЧ при W = w/w_p имеет место Т_n (1) = 1, |H(W)|² = 1/(1+d² ) и значением d задается коэффициент пульсаций в полосе передачи. При задании полосы по уровню А_p значение d рассчитывается аналогично фильтру Баттеруорта.

Соответственно, при задании А_s на границе полосы подавления, имеем:

1/(1+d² T_N ² (w_s /w_p )) = A_s ² . (10.4.4)

N = arcch[/d] / arcch(w_s /w_p ). (10.4.5)

Дальнейшие расчеты идентичны расчетам фильтров Баттеруорта, равно как и частотные преобразования фильтров ФНЧ в ФВЧ и ПФ.

Фильтры второго рода. Для фильтров Чебышева второго рода, с гладкой передаточной характеристикой в зоне пропускания и равноволновыми пульсациями в зоне подавления, используется функция:

|H(W)|² = 1/[1+d² (T_N ² (W_s )/T_N ² (W_s /W))], (10.4.6)

где W = w/w_p , W_s = w_s /w_p . Условие задания параметра d остается без изменений. На границе полосы подавления при w = w_s : 1+d² T_N ² (w_s /w_p ) = 1/A_s ² , откуда значение N также определяется аналогично фильтру первого рода. Дальнейший порядок расчетов фильтров Чебышева второго рода не отличается от фильтров первого рода.

Курсовая работа 17-07. Разработка программы расчета универсального частотного цифрового фильтра Чебышева (низкочастотный, высокочастотный, полосовой) и фильтрации цифровых сигналов.

10.5. Дополнительные сведения.

При использовании РЦФ очень часто упускается вопрос длительности фактического затухания переходного процесса. Между тем, для эффективного запуска РЦФ необходим поток входных данных x_n и множество начальных значений у_n . Если начальные значений у_n неизвестны и принимаются равными нулю, начальный переходной процесс включения неизбежен. При этом существует четкая тенденция - чем больше крутизна фильтра, тем дольше затухает переходной процесс. Поэтому РЦФ применяют, в основном, при обработке достаточно протяженных массивов. При обработке коротких массивов, длина которых соизмерима с длительностью переходного процесса РЦФ, необходим предварительный подбор начальных значений у_n . Проводится он, как правило, чисто эмпирически, с использованием различных наборов начальных данных.

Второй фактор, который следует учитывать - сдвиг фазы. Если при обработке данных сдвиг фазы входных сигналов недопустим, то следует применять либо дополнительный компенсирующий фильтр, восстанавливающий фазу обработанных сигналов, либо применять последовательную двойную фильтрацию однотипным рекурсивным фильтром с прямым и обратным проходом обрабатываемых данных.

литература

12. Канасевич Э.Р. Анализ временных последовательностей в геофизике. - М.: Недра, 1985.- 300 с.

18. Никитин А.А. Теоретические основы обработки геофизической информации: Учебник для вузов. - М.: Недра, 1986.- 342 с.

24. Хемминг Р.В. Цифровые фильтры. – М.: Недра, 1987. – 221 с.

Главный сайт автора Лекции по ЦОС Практикум

О замеченных опечатках, ошибках и предложениях по дополнению: davpro@yandex.ru.

Copyright ©2008 Davydov А.V.

Скачать архив с текстом документа