Теорема тейлора
СОДЕРЖАНИЕ: Теорема Тейлора ~ Степенной ряд ~ Основные разложения Теорема Тейлора (о разложении функции в степенной ряд). Функция, аналитическая в области комплексных чисел D, в окрестности каждой точки z0 этой области представляется в виде степенного ряда:Теорема Тейлора ~ Степенной ряд ~ Основные разложения
Теорема Тейлора (о разложении функции в степенной ряд).
Функция, аналитическая в области комплексных чисел D
, в окрестности каждой точки z
0
этой области представляется в виде степенного ряда
: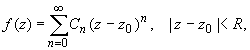 (1)
(1)
радиус сходимости R
которого не меньше, чем расстояние от точки z
0
до границы области D
.
Такой степенной ряд называется рядом Тейлора.
Коэффициенты ряда Тейлора вычисляются по формуле:
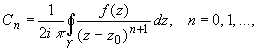 (2)
(2)
где ![]() - произвольный контур, принадлежащий области D
и охватывающий точку z
0
(в частности,
- произвольный контур, принадлежащий области D
и охватывающий точку z
0
(в частности, ![]() - окружность
- окружность ![]() ), или по формуле:
), или по формуле:
![]() (3)
(3)
Радиус сходимости ряда Тейлора равен расстоянию от точки z 0 до ближайшей особой точки функции.
Для вычисления радиуса сходимости ряда Тейлора можно также использовать формулы:
![]()
![]()
Основные разложения.
![]() (z
принадлежит области комплексных чисел);
(z
принадлежит области комплексных чисел);
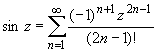 (z
принадлежит области комплексных чисел);
(z
принадлежит области комплексных чисел);
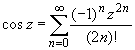 (z
принадлежит области комплексных чисел);
(z
принадлежит области комплексных чисел);
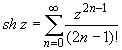 (z
принадлежит области комплексных чисел);
(z
принадлежит области комплексных чисел);
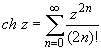 (z
принадлежит области комплексных чисел);
(z
принадлежит области комплексных чисел);
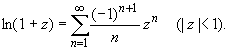
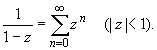
Пример 1 . Записать разложение по степеням z функции f (z ) = ch z .
Найдем производные функции:
f
(n)
(z
) = ch(n)
z
= ch z
при n= 2k
,
f
(n)
(z
) = ch(n)
z
= sh z
при n
= 2k
-1.
В данном примере z
0
= 0. По формуле (3) имеем:
Cn
= 0 при n
= 2k
; Cn
= 1/n
! при n
= 2k-
1;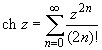 .
.
Так как ch z
- аналитическая функция в области действительных чисел, то радиус R
равен бесконечности. В результате имеем: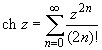 (z
принадлежит области действительных чисел).
(z
принадлежит области действительных чисел).
| Решение примера в среде пакета Mathcad | Теоретическая справка | |
| Решение примера в среде пакета Mathematica |
![]()
Пример 2 . Разложить по степеням (z -3) функцию f (z ) = sin z .
Обозначим z
-3 = t
. Используя тригонометрическую формулу для функции sin (3+t), получим:
sin(3+t
) = sin3 cos t
+cos3 sin t
.
Используя основные разложения, имеем:
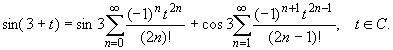
Так как t = z -3, то
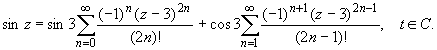
т.е. 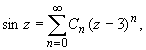
где ![]()
![]()
| Решение примера в среде пакета Mathcad | Теоретическая справка | |
| Решение примера в среде пакета Mathematica |
![]()
Пример 3
. Разложить по степеням z
функцию ![]()
Дробь правильная. Раскладываем ее на элементарные дроби:
![]()
Раскладываем элементарные дроби по степеням z
:
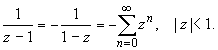
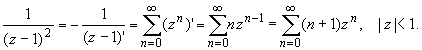
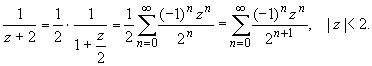
Для исходной дроби получаем разложение:
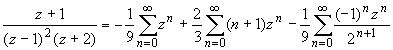
или, складывая ряды:
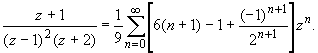
Окончательный ответ:
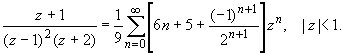
Теорема Лорана (о разложении функции в ряд по целым степеням).
Функция f
(z
), аналитическая в кольце
r
| z
- z
0
| R
, ![]()
представляется в этом кольце сходящимся рядом по целым степеням, т.е. имеет место равенство: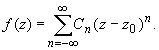 (1)
(1)
Коэффициенты ряда вычисляются по формуле: 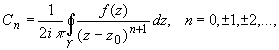 (2)
(2)
где ![]() - произвольный контур, принадлежащий кольцу и охватывающий точку z
0
; в частности,
- произвольный контур, принадлежащий кольцу и охватывающий точку z
0
; в частности, ![]() - окружность
- окружность ![]()
Ряд (1), коэффициенты которого вычисляются по формуле (2), называется рядом Лорана функции f (z ).
Совокупность членов ряда с неотрицательными степенями 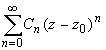 называется правильной частью ряда Лорана, члены с отрицательными степенями образуют главную часть ряда Лорана:
называется правильной частью ряда Лорана, члены с отрицательными степенями образуют главную часть ряда Лорана: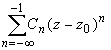 или
или 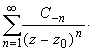
Для коэффициентов ряда имеет место формула оценки коэффициентов - неравенство Коши:![]() где
где ![]()
r - радиус контура интегрирования в формуле (2).
На границах кольца сходимости ряда Лорана есть хотя бы по одной особой точке функции f (z ) - его суммы.
Частными случаями рядов Лорана являются разложения функции в окрестности особой точки z
0
(r
= 0) и в окрестности бесконечно удаленной точки (z
0
= 0, ![]() ).
).
При построении разложений в ряд Лорана используются разложения в степенные ряды (ряды Тейлора), используются основные разложения и арифметические операции со сходящимися рядами.
Пример 1. Разложить функцию ![]() в ряд Лорана по степеням z
.
в ряд Лорана по степеням z
.
Решение.
Так как функция является рациональной дробью, то особыми точками являются нули знаменателя, т.е. z
1
= -1 и z
2
= 3. Запишем функцию в виде![]()
Кольца аналитичности | z | 1, 1 | z | 3, | z | 3.
Раскладываем дробь на элементарные дроби:![]()
При | z
| 1 имеем: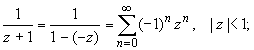
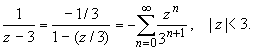
Таким образом, в круге | z
| 1 функция раскладывается в ряд Тейлора: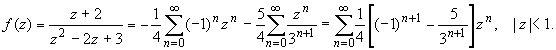
В кольце 1 | z
| 3: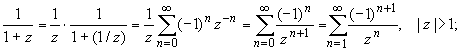
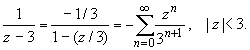
В итоге имеем: 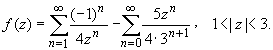
В круге | z
| 3: 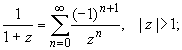
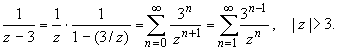
В итоге имеем: 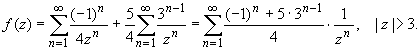
| Решение примера в среде пакета Mathcad | Теоретическая справка | |
| Решение примера в среде пакета Mathematica |
![]()
Пример 2. Разложить функцию f (z ) = z 3 ·e 1/z в окрестности точки z 0 = 0.
Решение.
Из основного разложения ![]() получаем
получаем
![]()
![]()
или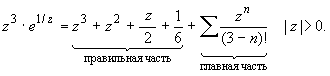
Вычет функции ~ Вычисление вычетов
Вычетом функцииf(z) в изолированной особой точке z
0
(точка принадлежит области комплексных чисел) называется интеграл вида: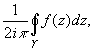
где ![]() - контур, принадлежащий окрестности точки z
0
и охватывающий ее. Обход контура - положительный, т.е. область ограниченная им и принадлежащая окрестности z
0
при обходе расположена слева: обход против часовой стрелки.
- контур, принадлежащий окрестности точки z
0
и охватывающий ее. Обход контура - положительный, т.е. область ограниченная им и принадлежащая окрестности z
0
при обходе расположена слева: обход против часовой стрелки.
Обозначается вычет 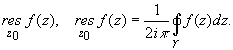
Вычет функции в конечной изолированной особой точке равен коэффициенту С
-1
при первой отрицательной степени в разложении функции в ряд Лорана в окрестности этой точки, т.е. при 1/(z
-z
0
) для z
0
, принадлежащей области комплексных чисел: ![]()
ПРИМЕР 1. Вычисление вычета функции в ее конечных особых точках.
Если конечная особая точка z
0
является устранимой особой точкой функции f
(z
), то ![]()
ПРИМЕР 2. Вычисление вычета в устранимой особой точке.
Если z
0
- полюс порядка n
функции f
(z
), z
0
принадлежит области комплексных чисел, то ![]()
![]()
ПРИМЕР 3. Вычисление вычета в полюсе порядка n.
Если z
0
- простой полюс функции ![]() ,
,
где ![]() аналитические функции в точке z
0
и
аналитические функции в точке z
0
и ![]() ,
,
то ![]()
ПРИМЕР 4. Вычисление вычета в простом полюсе.
Если z 0 - существенно особая точка функции f (z ), то вычет в ней находится, исходя из определения, т.е. как С -1 - коэффициент в разложении f (z ) в ряд Лорана в окрестности z 0 .
ПРИМЕР 5. Вычисление вычета в существенной особой точке.
Пример 1. Вычислить вычет функции f (z) = (z+2)/(z2 -2z-3) в точке z = 3.
Решение.
Разложим функцию в ряд Лорана по степеням z - 3: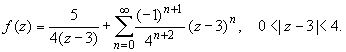
Из этого разложения находим ![]()
Заметим, что здесь точка z = 3 - простой полюс.
| Решение примера в среде пакета Mathcad | Теоретическая справка | |
| Решение примера в среде пакета Mathematica |
![]()
Пример 2. Вычислить вычет функции f(z) в точке z = 0, ![]()
Решение.
Запишем 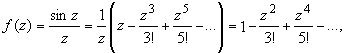
т.е. z= 0 - устранимая особая точка. Следовательно, ![]()
| Решение примера в среде пакета Mathcad | Теоретическая справка | |
| Решение примера в среде пакета Mathematica |
![]()
Пример 3. Вычислить вычет функции ![]()
Так как ![]() то z
= 0 для f
(z
) - полюс второго порядка. Следовательно,
то z
= 0 для f
(z
) - полюс второго порядка. Следовательно, 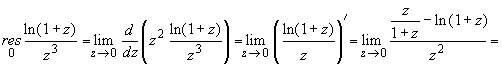
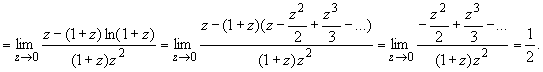
| Решение примера в среде пакета Mathcad | Теоретическая справка | |
| Решение примера в среде пакета Mathematica |
![]()
Пример 4 . Вычислить вычет функции f(z) = ctg 2z во всех ее особых точках.
Решение.
В точках ![]() данная функция имеет полюсы первого порядка (простые полюсы), поскольку
данная функция имеет полюсы первого порядка (простые полюсы), поскольку
![]()
![]()
Следовательно, 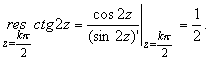
| Решение примера в среде пакета Mathcad | Теоретическая справка | |
| Решение примера в среде пакета Mathematica |
![]()
Пример 5
. Вычислить вычет функции ![]()
Решение.
Разложим замкнутую функцию в ряд Лорана в окрестности z
= 1: 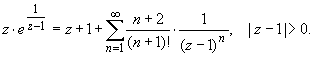
Из этого разложения следует, что z
= 1 является существенной особой точкой и
С
-1
= 3/2, т.е. 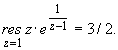
Теорема о вычетах ~ Примеры
Теорема (Основная теорема о вычетах).
Если функция f
(z
- аналитична в ![]() за исключением конечного числа особых точек
за исключением конечного числа особых точек ![]() , то справедливо равенство
, то справедливо равенство ![]()
где D
- односвязная область в комплексной плоскости, ![]() - граница D
,
- граница D
, ![]() - вычет функции f
(z
) в точке zk
.
- вычет функции f
(z
) в точке zk
.
ПРИМЕР 1. Вычисление интеграла по теореме о вычетах.
ПРИМЕР 2. Вычисление интеграла по теореме о вычетах.
ПРИМЕР 3. Вычисление интеграла по теореме о вычетах.
Пример 1. Вычислить интеграл ![]()
Решение.
Особыми точками подынтегральной функции являются нули знаменателя - корни уравнения exp(z
) - i =
0, т.е. точки ![]()
Кругу ![]() принадлежит только одна из этих точек, точка
принадлежит только одна из этих точек, точка ![]()
Эта точка - простой полюс функции ![]() , т.к. она является простым нулем знаменателя.
, т.к. она является простым нулем знаменателя.
Вычислим вычет в простом полюсе f (z ):
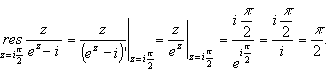
Тогда ![]()
| Решение примера в среде пакета Mathcad | Теоретическая справка | |
| Решение примера в среде пакета Mathematica |
![]()
Пример 2. Вычислить интеграл 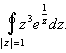
Решение. Единственная особая точка подынтегральной функции - существенно особая точка z = 0. Она принадлежит области, ограниченной контуром интегрирования.
Вычислим вычет в существенно особой точке функции f
(z
): ![]() поскольку
поскольку
![]()
![]()
Тогда 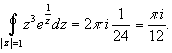
| Решение примера в среде пакета Mathematica | Теоретическая справка |
![]()
Пример 3. Вычислить интеграл ![]()
Решение.
Особыми точками подынтегральной функции являются нули знаменателя - корни уравнения z
4
+ 1 =
0, т.е. точки ![]()
Все эти точки - простые полюсы подынтегральной функции, кругу ![]() принадлежат только две из них:
принадлежат только две из них: ![]() и
и ![]()
Вычислим вычеты f (z ) в этих точках:
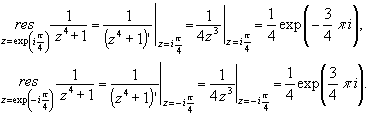
Тогда
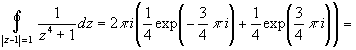
![]()
![]()