Теоретические основы электротехники
СОДЕРЖАНИЕ: Министерство образования и науки Украины Донбасский государственный технический университет Кафедра “Теоретические основы электротехники” КОНТРОЛЬНОЕ ЗАДАНИЕ №2Министерство образования и науки Украины
Донбасский государственный технический университет
Кафедра “Теоретические основы электротехники”
КОНТРОЛЬНОЕ ЗАДАНИЕ №2
по курсу: “Теоретические основы электротехники”
Вариант №25
Выполнил:
студент гр.
Проверил:
старший преподаватель
Алчевск 2009
КОНТРОЛЬНОЕ ЗАДАНИЕ №2
Определить токи в ветвях и напряжение на конденсаторе во время переходного процесса в данной схеме (схема 1). Построить графики зависимости этих величин от времени.
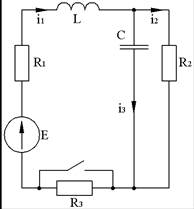
Переходный процесс рассчитать двумя методами: классическим и операторным.
Дано:
![]()
![]()
![]()
![]()
![]()
![]()
РЕШЕНИЕ:
До коммутации ![]() :
:
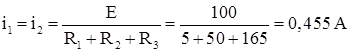
![]()
Принужденные значения (после окончания переходного процесса):
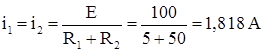
![]()
КЛАССИЧЕСКИЙ МЕТОД
Входное сопротивление:
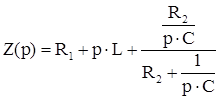
Характеристическое уравнение:
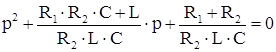
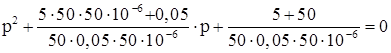
![]()
![]()
![]() ;
; ![]()
Находим ток ![]() :
:
![]()
Постоянные ![]() находим по начальным условиям:
находим по начальным условиям:
1. ![]() , отсюда
, отсюда ![]()
2. По 2-ому закону Кирхгофа:
![]() , отсюда
, отсюда ![]()
![]() ,
,
следовательно ![]()
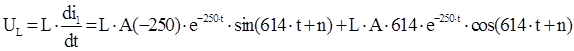
![]()
Получаем систему уравнений:
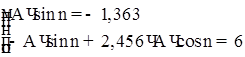
Отсюда ![]() ,
, ![]()
![]()
Напряжение на конденсаторе находим по 2-ому закону Кирхгофа:
![]()
![]()
![]()
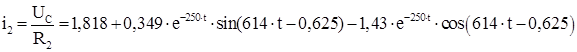
По 1-ому закону Кирхгофа:
![]()
![]()
ОПЕРАТОРНЫЙ МЕТОД
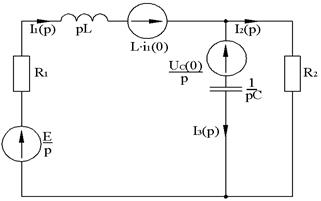
Составим систему уравнений по законам Кирхгофа:
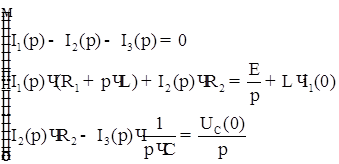
Главный определитель системы:
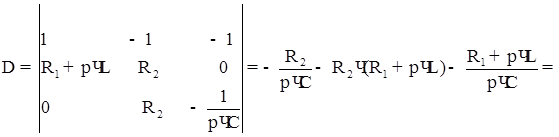
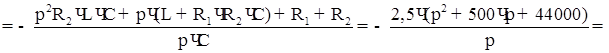
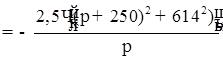
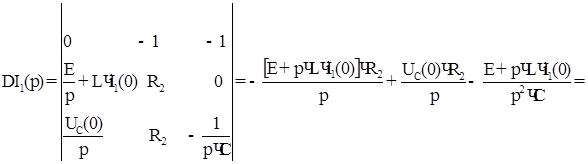
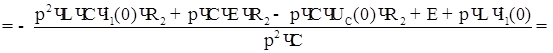
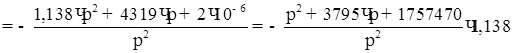
Изображение тока:
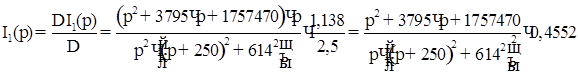
По таблице преобразований Лапласа находим оригинал тока в виде:
![]()
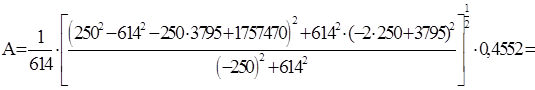
![]()
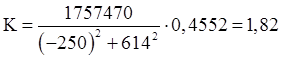
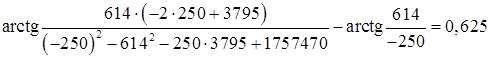
Ответы двумя способами получились одинаковыми.
Рассчитываем зависимости ![]() ,
, ![]() ,
, ![]() и
и ![]() от времени. Расчет сводим в таблицу:
от времени. Расчет сводим в таблицу:
| t, c |
|
|
|
|
| 0 |
0,45 |
0,45 |
0 |
22,73 |
| 0,002 |
2,62 |
1,22 |
1,4 |
61,2 |
| 0,004 |
2,65 |
2,08 |
0,57 |
103,9 |
| 0,006 |
1,86 |
2,14 |
-0,28 |
107,1 |
| 0,008 |
1,53 |
1,86 |
-0,32 |
92,8 |
| 0,01 |
1,69 |
1,71 |
-0,02 |
85,7 |
| 0,012 |
1,87 |
1,76 |
0,11 |
88,1 |
| 0,014 |
1,89 |
1,83 |
0,06 |
91,7 |
| 0,016 |
1,83 |
1,85 |
-0,02 |
92,3 |
| 0,018 |
1,8 |
1,82 |
-0,02 |
91,2 |
| 0,02 |
1,81 |
1,81 |
0 |
90,5 |
КОНТРОЛЬНОЕ ЗАДАНИЕ №5
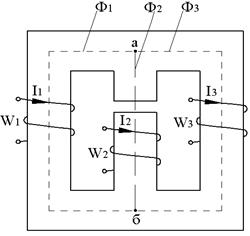
Определить магнитный поток и индукцию в участках магнитной цепи. Числа витков ![]() .
.
РЕШЕНИЕ
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Применяем метод двух узлов. Показываем магнитные потоки. Принимаем направление узлового напряжения ![]() от узла «а» к узлу «б». Уравнение по законам Кирхгофа:
от узла «а» к узлу «б». Уравнение по законам Кирхгофа:
![]()
![]()
![]()
![]()
Выражаем ![]() из этих уравнений:
из этих уравнений:
![]()
![]()
![]()
Строим зависимости ![]() ,
, ![]() ,
, ![]() .
.
Задаем значения токов и находим индукции на всех участках:
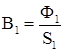 ;
; 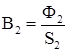 ;
; 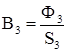
по кривой намагничивания находим напряженности.
Результаты вычислений представлены в таблице. Строим также вспомогательную кривую ![]() .
.
Точка пересечения вспомогательной кривой и графика ![]() дает решение задачи.
дает решение задачи.
|
|
|
|
|
|
|
|
|
|
| 0 |
0 |
0 |
0 |
960 |
0 |
0 |
0 |
0 |
| 0,48 |
0,4 |
53 |
-5,3 |
955 |
0,6 |
0,4 |
53 |
318310 |
| 0,96 |
0,8 |
135 |
-13,5 |
946 |
1,2 |
0,8 |
135 |
636620 |
| 1,2 |
1,0 |
200 |
-20 |
940 |
1,5 |
1,0 |
200 |
795775 |
| 1,44 |
1,2 |
475 |
-47,5 |
913 |
1,8 |
1,2 |
475 |
954930 |
| 1,68 |
1,4 |
1060 |
-106 |
854 |
||||
| 1,8 |
1,5 |
2000 |
-200 |
760 |
||||
| 1,92 |
1,6 |
5000 |
-500 |
460 |
||||
| 2,04 |
1,7 |
9000 |
-900 |
60 |
||||
| 2,16 |
1,8 |
14000 |
-1400 |
-440 |
При этом ![]() А. По графикам определяем магнитные потоки:
А. По графикам определяем магнитные потоки:
![]() Вб;
Вб;
![]() Вб;
Вб;
![]() Вб.
Вб.
Схема состоит из источника синусоидального тока ![]() , линейного активного сопротивления, линейной емкости (индуктивности), и нелинейной индуктивности (емкости), вебер-амперная (кулон-вольтная) характеристика которой приведена. Требуется рассчитать и построить зависимости
, линейного активного сопротивления, линейной емкости (индуктивности), и нелинейной индуктивности (емкости), вебер-амперная (кулон-вольтная) характеристика которой приведена. Требуется рассчитать и построить зависимости ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() в функции
в функции ![]() . Значения исходных величин для соответствующего варианта.
. Значения исходных величин для соответствующего варианта.
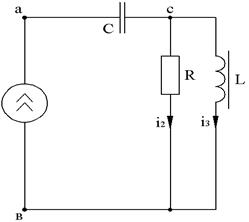
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
РЕШЕНИЕ
Вебер-амперная характеристика нелинейной индуктивности (![]() Вб):
Вб):
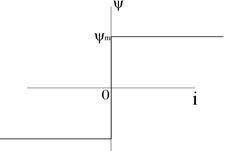
В интервале времени ![]() происходит перемагничивание катушки. При этом
происходит перемагничивание катушки. При этом ![]() , весь ток проходит через резистор:
, весь ток проходит через резистор:
![]()
Амплитуда напряжений на конденсаторе и резисторе
![]()
Напряжение на конденсаторе на 90° опережает ток:
![]()
Напряжение на резисторе совпадает по фазе с током:
![]()
![]()
Находим потокосцепление:
![]()
![]() , отсюда получаем,
, отсюда получаем,
интегрируя уравнение:
![]()
Постоянную С находим из условия:
при t=0 ![]() , отсюда
, отсюда ![]() ,
, ![]()
![]()
Время ![]() определяем из условия, что при этом
определяем из условия, что при этом ![]() :
:
![]()
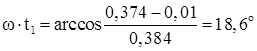
В интервале времени ![]() потокосцепление катушки
потокосцепление катушки ![]() , напряжение не катушки
, напряжение не катушки ![]() ,
, ![]() , весь ток проходит через катушку:
, весь ток проходит через катушку:
![]()
![]()
В интервалах ![]() и
и ![]() процессы протекают аналогично.
процессы протекают аналогично.
По полученным формулам строим графики.