Теория поля и элементы векторного анализа
СОДЕРЖАНИЕ: Элементы математической теории скалярных и векторных полей Математическая теория поля занимается изучением его свойств, отвлекаясь от его конкретного физического смысла. Поэтому получаемое в этой теории понятие и закономерности относятся ко всем конкретным полям.Элементы математической теории скалярных и векторных полей
Математическая теория поля занимается изучением его свойств, отвлекаясь от его конкретного физического смысла. Поэтому получаемое в этой теории понятие и закономерности относятся ко всем конкретным полям.
Определение 1
Полем называется совокупность значений той или иной величины (скорость, плотность, давление и т.п.), заданных в каждой точке рассматриваемой области.
Если рассматриваемая величина
а) скаляр , то поле называется скалярным, например
![]() – поле плотности
– поле плотности
б) вектор , то поле называется векторным
![]() – поле скоростей
– поле скоростей
в) тензор , то поле называется тензорным
![]() – поле напряжений.
– поле напряжений.
Определение 2
Если значения рассматриваемых величин не изменяются
во времени
, то поле называется стационарным
(установившимся), если же они ![]() изменяются
во времени
, то поле называется нестационарным.
изменяются
во времени
, то поле называется нестационарным.
Здесь мы остановимся на рассмотрении свойств стационарных полей.
Скалярное поле 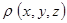
Характеристики скалярного поля
1) Скалярное поле характеризуется поверхностью уровня
![]() (см. рис.)
(см. рис.)
2) Градиент поля определяется как вектор, составленный из частных производных
![]() (1)
(1)
Он направлен по нормали к поверхностям уровня и характеризует величину и направление наибыстрейшего изменения величины поля. Полный дифференциал скалярного поля ![]() можно представить в виде:
можно представить в виде:
![]() , (2)
, (2)
где ![]() .
.
3) Производная по направлению
![]() (см. рис. 2) определяется как проекция градиента на данное направление
(см. рис. 2) определяется как проекция градиента на данное направление
![]() (3)
(3)
Частный случай: производная по нормали :
![]() (4)
(4)
4) Частные и полные производные по времени
Рассмотрим нестационарное скалярное поле:
![]()
Скорость изменения r в фиксированной точке ![]() равна
равна ![]() и называется частной
производной (локальной
производной). Пусть задана некоторая траектория в пространстве, где определено скалярное поле (рис. 3)
и называется частной
производной (локальной
производной). Пусть задана некоторая траектория в пространстве, где определено скалярное поле (рис. 3)
![]()
![]()
Скорость изменения r вдоль траектории определяется как полная производная по t от сложной функции и равна:
![]() (5)
(5)
![]() – конвективная производная, она связана с перемещением точки (частицы) из одной точки пространства в другую.
– конвективная производная, она связана с перемещением точки (частицы) из одной точки пространства в другую.
Замечание :
Оператор «набла » – это греческое слово, означающее «арфа» – музыкальный инструмент, по форме напоминающий перевернутый треугольник.
Характеристики векторного поля ![]()
1) Векторная линия
– кривая, направление которой в каждой ее точке совпадает с направлением вектора ![]() , отвечающего этой точке (см. рис. 4)
, отвечающего этой точке (см. рис. 4) ![]()
![]() и
и ![]()
– коллинеарные (параллельные) векторы и, следовательно,
![]() || =
|| = ![]()
![]() = l
= l![]()
![]() = l
= l
![]() (6)
(6)
2) Производная от вектора по направлению определяется следующим образом:
![]() (7)
(7)
![]() – направляющие косинусы вектора
– направляющие косинусы вектора ![]() , в декартовой системе координат.
, в декартовой системе координат.
Доказательство :
Учтем, что
![]()
и так далее, подставим в ![]() , получим:
, получим:
![]()
+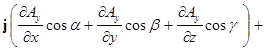
+![]()
![]()
Итак, мы доказали
![]() .
.
3) Частная и полная производные по времени от вектора
![]() (9)
(9)
Доказательство :
![]()
![]()
![]()
4) Поток вектора через поверхность. Дивергенция
![]() – поток векторной величины через элементарную площадку (элементарный поток)
– поток векторной величины через элементарную площадку (элементарный поток)
![]() (11)
(11)
векторный поток через незамкнутую площадку;
![]() (12)
(12)
поток вектора через замкнутую площадку.
![]() –
–
поток вектора скорости через поверхность S равен объему жидкости, протекающей через эту площадку поверхности за единицу времени.
По теореме Остроградского-Гаусса (рис. 7)
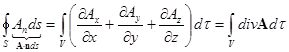 (13)
(13)
Сжимая объем ![]() и, следовательно
и, следовательно ![]() получим, используя теорему осреднения
получим, используя теорему осреднения
![]() (14)
(14)
Следовательно, ![]() можно определить как предел
можно определить как предел
 (15)
(15)
Пример :
В гидродинамике поле скоростей ![]() имеет
имеет
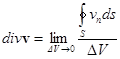
дивергенция равна количеству жидкости, рассчитанному на единицу объема, вытекающему из данной точки пространства за одну секунду, т.е. ![]() равна мощности источника жидкости (если
равна мощности источника жидкости (если ![]() 0).
0).
Если ![]() 0, то в этих точках пространства расположен сток жидкости, с мощностью
0, то в этих точках пространства расположен сток жидкости, с мощностью ![]() .
.
5. Циркуляция вектора вдоль линии
Роток векторного поля
Элементарная циркуляция вектора ![]() вдоль линии dl
равна (рис. 8а)
вдоль линии dl
равна (рис. 8а)
![]() (16)
(16)
Циркуляция вектора ![]() вдоль замкнутой линии L
(рис. 8б)
вдоль замкнутой линии L
(рис. 8б)
![]() (17)
(17)
Пусть контур L ограничивает некоторую поверхность S (рис. 8в). Используем теорему Стокса и преобразуем интеграл по кривой L в интеграл по поверхности S :
![]() (18)
(18)
Роток (вихрь) вектора ![]() определяется как
определяется как
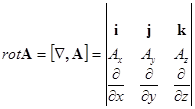 (19)
(19)
Определение
Циркуляция
вектора ![]() вдоль замкнутого контура равна потоку его ротора
через поверхность, ограниченную этим контуром (рис. 9)
вдоль замкнутого контура равна потоку его ротора
через поверхность, ограниченную этим контуром (рис. 9)
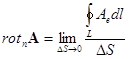 (20)
(20)
Потенциальное векторное поле
Определение :
Векторное поле ![]() называется потенциальным, если существует скалярная величина
называется потенциальным, если существует скалярная величина ![]() , такая, что
, такая, что
![]()
![]() – называется скалярным потенциалом поля.
– называется скалярным потенциалом поля.
Свойства потенциального поля
1. В потенциальном поле отсутствуют вихри (отсутствует ротация), т.е.
![]()
Доказательство:
![]()
2. Циркуляция по любому замкнутому контуру равна нулю (это следствие п.1)
![]()
3. Работа потенциального поля при перемещении точки из одного положения в другое не зависит от пути соединяющего эти положения и равна разности потенциалов в конечных точках.
Циркуляция потенциального поля не зависит от вида кривой, соединяющей две различные точки, и равна разности значений потенциала в данных точках.
![]()
отсюда получаем
![]()
![]()
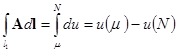
4. Векторные линии потенциального поля не могут быть замкнутыми.
Доказательство от противоположного:
Допустим, что есть замкнутая векторная линия L
. Тогда по определению векторной линии вдоль соответствующего контура ![]() и, следовательно, и циркуляция по нему больше нуля
и, следовательно, и циркуляция по нему больше нуля ![]() , что противоречит свойству 2.
, что противоречит свойству 2.
5. Сумма потенциальных векторных полей является потенциальным полем, и потенциал суммы полей равен сумме потенциалов.
Соленоидальное векторное поле
Определение :
Векторное поле![]() называется соленоидальным (вихревым), если существует векторная величина
называется соленоидальным (вихревым), если существует векторная величина ![]() такая, что
такая, что
![]() = rot
= rot
![]()
![]() – называется векторным потенциалом поля
– называется векторным потенциалом поля ![]() .
.
Свойства соленоидального поля
1. Для того чтобы поле ![]() было соленоидальным, необходимо и достаточно, чтобы во всей рассматриваемой области выполнялось равенство div
было соленоидальным, необходимо и достаточно, чтобы во всей рассматриваемой области выполнялось равенство div
![]() = 0, т.е. его поток через всякую замкнутую поверхность, погруженную в поле, = 0. Следовательно, соленоидальные поля лишены источников и стоков.
= 0, т.е. его поток через всякую замкнутую поверхность, погруженную в поле, = 0. Следовательно, соленоидальные поля лишены источников и стоков.
Замечание : Это свойство можно положить в определение.
Доказательство основывается на том, что
![]() =
=
Следствие ![]() = 0
= 0
![]()
как следствие этого свойства получаем, что поток вектора ![]() соленоидального поля через две одинаково ориентированные поверхности S
1
и S
2
, опирающиеся на один и тот же контур L
, одинаков.
соленоидального поля через две одинаково ориентированные поверхности S
1
и S
2
, опирающиеся на один и тот же контур L
, одинаков.
2. Поток соленоидального поля через два любых сечения векторной трубки одинаков.
Доказательство:
Отрезок векторной трубки, ограниченный сечениями S
1
, S
2
и S
d
, можно рассматривать как замкнутую поверхность, помещенную в соленоидальное поле. Поэтому ![]()
![]() , но
, но ![]() , т.к.
, т.к. ![]() .
.
Учитывая, что ![]() и
и ![]() направлены в противоположные стороны, и вводя (–
направлены в противоположные стороны, и вводя (–![]() ), получим
), получим
![]() отсюда следует
отсюда следует ![]()
3. В соленоидальном поле векторные линии либо замкнуты, либо уходят к границе поля. Так как ![]() , то векторные линии поля
, то векторные линии поля ![]() не могут начинаться или кончаться в области поля, иначе в…? будет существовать сток или исток, что противоречит свойству 1.
не могут начинаться или кончаться в области поля, иначе в…? будет существовать сток или исток, что противоречит свойству 1.
4. Сумма соленоидальных векторных полей есть соленоидальное поле.
Потенциальное несжимаемое поле. Гармоническое поле
![]() ,
, ![]() отсюда следует
отсюда следует ![]() =
=![]()
![]()
![]()
Это поле часто называют гармоническим или полем Лапласа.
Резюме
По заданному полю ![]() мы всегда можем найти поля u
и
мы всегда можем найти поля u
и ![]() . Справедливо и обратное утверждение: по известным u
и
. Справедливо и обратное утверждение: по известным u
и ![]() всегда можно найти искомое поле
всегда можно найти искомое поле ![]() .
.
Пусть поле ![]() известно, тогда потенциалы u
и
известно, тогда потенциалы u
и ![]() находятся из уравнений:
находятся из уравнений:
![]()
![]()
Если u
и ![]() известны, тогда векторное поле
известны, тогда векторное поле ![]() определяется из уравнений:
определяется из уравнений:
![]()
Эти уравнения всегда разрешимы.
Теорема о разложимости произвольного векторного поля
Произвольное векторное поле ![]() всегда может быть представлено в виде суммы потенциального
всегда может быть представлено в виде суммы потенциального ![]() и соленоидального
и соленоидального ![]() полей.
полей.
Задано
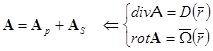
где ![]() ;
; ![]()
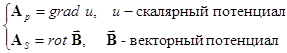
и, следовательно ![]()
Потенциалы ![]() и u
должны удовлетворять следующему соотношению:
и u
должны удовлетворять следующему соотношению:
1. ![]()
но дивергенция соленоидального поля должна быть равна 0.
![]()
отсюда
![]()
![]()
2. ![]()
![]() (**)
(**)
Для определения ![]() и u
получили два дифференциальных уравнения, которые всегда имеют решения и, следовательно, произвольное поле
и u
получили два дифференциальных уравнения, которые всегда имеют решения и, следовательно, произвольное поле ![]() всегда можно представить в виде суммы потенциального
и соленоидального
полей.
всегда можно представить в виде суммы потенциального
и соленоидального
полей.
Нахождение векторного поля по его характеристикам
Для нахождения ![]() и u
нужно решить систему четырех уравнений
и u
нужно решить систему четырех уравнений
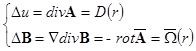
Пусть известны характеристики векторного поля ![]()
![]() (1)
(1)
или в интегральной форме:
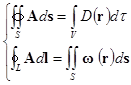
Будем искать распределение поля ![]() . Для этого разложим его на потенциальное
. Для этого разложим его на потенциальное ![]() и вихревое
и вихревое ![]() .
.
![]() =
= ![]() +
+ ![]() (2)
(2)
Подставляя (2) в уравнение (1), получим систему уравнений для отыскания ![]() :
:
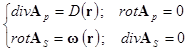 (3)
(3)
Потенциальное поле удобно представить через градиент
![]() (4)
(4)
т.к. в этом случае приходится находить всего лишь одну скалярную величину вместо трех. Подставляем (4) в первое уравнение (3), получаем уравнение
![]() – уравнение Пуассона (5)
– уравнение Пуассона (5)
Его решение известно и имеет следующий вид:
![]() . (6)
. (6)
Соленоидальное (вихревое) поле будем искать через векторный потенциал
![]() (7)
(7)
Тогда для ![]() получаем следующее уравнение:
получаем следующее уравнение:
![]() (8)
(8)
Т.к. поле ![]() тоже векторное, то для его нахождения кроме rot
необходимо задать еще одно условие на div
тоже векторное, то для его нахождения кроме rot
необходимо задать еще одно условие на div
![]() . В качестве такого условия (которое заранее ниоткуда не вытекает) удобно выбрать div
. В качестве такого условия (которое заранее ниоткуда не вытекает) удобно выбрать div
![]() = 0 (это называется калибровкой Кирхгофа). В этом случае уравнение (8) упрощается
= 0 (это называется калибровкой Кирхгофа). В этом случае уравнение (8) упрощается
![]() (8а)
(8а)
и его решение имеет вид:
![]() (9)
(9)
Следовательно, искомое поле ![]() равно:
равно:
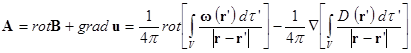
Интегральные соотношения теории векторного поля
1. Теорема Остроградского-Гаусса
![]()
2. Теорема Стокса
![]()
3. Теорема Грина
(первая форма)
![]()
(вторая форма)
![]()
4. Интеграл от скаляра по замкнутому контуру
![]()
5. Интеграл от ![]() по объему
по объему
![]()
![]()
Используя теорему о среднем при ![]() находим
находим
![]()
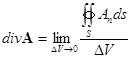
![]() – источник
– источник
![]() – сток
– сток
6. Циркуляция вектора вдоль линии
Роток векторного поля
![]() – элементарная циркуляция вектора вдоль линии L
– элементарная циркуляция вектора вдоль линии L
![]() – циркуляция вектора вдоль замкнутой линии.
– циркуляция вектора вдоль замкнутой линии.
Теорема Стокса
![]()
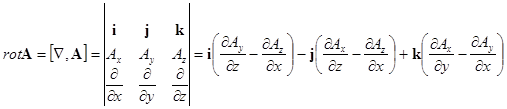
Механический смысл ротора векторного поля
Рассмотрим движение твердого тела. Линейная скорость ![]() произвольной точки
произвольной точки ![]() равна твердого тела равна
равна твердого тела равна ![]()
где ![]() – скорость полюса
– скорость полюса ![]()
![]() – мгновенная угловая скорость
– мгновенная угловая скорость
![]()
Представим
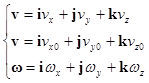
Следовательно, компоненты скоростей т.М равны
![]()
![]()
![]()
В фиксированный момент времени t
переменными являются только координаты т. ![]() , все остальные величины
, все остальные величины ![]() ,
, ![]()
![]() являются постоянными
являются постоянными
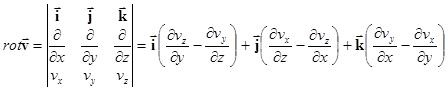 =
=
![]()
Дифференцирование скалярных и векторных полей
Скалярное поле ![]()
![]()
![]()
Векторное поле ![]()
![]()
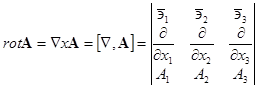
![]()
Таблица 1. Операции 2-го порядка
| Скалярное поле j | Векторное поле А | ||
grad |
нет |
|
нет |
| div | Нет | ||
| rot | нет | ||
Таблица 2. Дифференцирование произведений
grad |
нет |
|
нет |
| div | нет | ||
| rot | нет |
|