Теория вероятностей

СОДЕРЖАНИЕ: Способы применения теорий вероятности в практической статистике. Решение задач с применением математической статистики: теоремы появления независимых событий, формулы полной вероятности, формулы Бернулли. Постороение статистических таблиц и графиков.

Задание 1

Вероятность того, что студент сдаст первый экзамен равна 0,7; второй – 0,95; третий – 0,45. Вычислить вероятность того, что студент сдаст:

а) один экзамен;

б) ни одного экзамена;

в) хотя бы два экзамена.

Решение:

а) Введем обозначения:

событие А – «студент сдаст только один экзамен»;

событие А1 - «студент сдаст 1-ый экзамен»

событие А2 - «студент сдаст 2-ой экзамен»

событие А3 - «студент сдаст 3-ий экзамен»

В соответствии с условием задачи:

Р(А1 )=0,7 Р(А2 )=0,95 Р(А3 )=0,45

Тогда противоположные события, т.е. события «студент не сдаст i-ый экзамен» , имеют вероятности, соответственно:

, ,

Событие А можно представить в виде:

Указанные слагаемые представляют собой несовместные события, поэтому по теореме сложения вероятностей несовместных событий имеем:

.

Так как события независимые, то, применяя теорему умножения вероятностей независимых событий, имеем:

Таким образом, вероятность того, что студент сдаст только один экзамен, равна

б) Введем обозначения:

событие В – «студент не сдаст ни одного экзамена»;

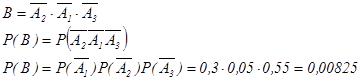
Таким образом, вероятность того, что студент не сдаст ни одного экзамена, равна

в) Введем обозначения:

событие С – «студент сдаст хотя бы два экзамена»,

Так как в результате данного испытания могут появиться три события: , то появление хотя бы двух из них означает наступление либо двух, либо трех событий.

Следовательно, применяя теорему появления независимых событий, имеем:

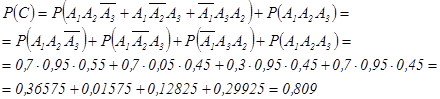
Таким образом, вероятность того, что студент сдаст хотя бы два экзамена, равна

Ответ: ; ;

Задание 2

На фабрике производятся швейные изделия. Вероятность появления брака равна 0,10. Была введена упрощенная сиситема контроля изделий, состоящая из двух независимых проверок. В результате k -ой проверки ( k =1, 2) изделие удовлетворяющее стандарту, отбраковывается с вероятностью, , а бракованное изделие принимается с вероятностью . Изделие принимается, если оно прошло обе проверки. Найти вероятности событий:

а) бракованное изделие будет принято;

б) изделие, удовлетворяющее стандарту, будет отбраковано;

в) случайно взятое на проверку швейное изделие будет отбраковано;

г) отбракованное изделие удовлетворяет стандарту;

д) из 5 изделий, взятых на проверку, 1 изделие будет удовлетворять стандарту.

; ; ;

Решение:

Пусть А – событие, состоящее в том, что изделие удовлетворяет стандарту, - изделие не удовлетворяет стандарту, - изделие принимается при k-ой проверке; - изделие бракуется при k-ой проверке.

а) определим вероятность того, что бракованное изделие будет принято. Так как заранее известно, что изделие с браком, то вероятность события не учитывается. Чтобы это изделие было принято, должно произойти событие , т.е. бракованное изделие принимается полсе обеих проверок. Вероятность этого события равна:

б) найдем вероятность того, что изделие, удовлетворяющее стандарту, будет отбраковано. Здесь известно по условию, что оно уже удовлетворяет стандарту. Значит соответствующее событие будет равно сумме двух событий: 1 – изделие отбраковано при первой проверке ; 2 – изделие было принято при первой проверке, но отбраковано при второй: . Знаяит вероятность будет равна:

в) пусть С – событие, состоящее в том, что случайно взятое изделие на проверку будет отбраковано. Изначально нам не известно, какое изделие идет на проверку.

Возможны две гипотезы:

Н1 – на проверку идет изхделие, удовлетворяющее стандарту;

Н2 – на проверку идет бракованное изделие.

По условию,

Р(Н1 )=1-р=1-0,10=0,90

Р(Н2 )=р=0,10

Вероятность искомого события найдем по формуле полной вероятности. Если событие может произойти лишь при условии наступления какого-либо из несовместных событий-гипотез, образующих полную группу (т.е. какое-то одно из них обязательно наступает), то его вероятность равна сумме произведений вероятностей этих гипотез на условные вероятности искомого события при условии, что соответствующие гипотезы произошли. Таким образом, при двух гипотезах

Р(С)=Р(Н1 )Р(С/Н1 )+Р(Н2 )Р(С/Н2 )

Р(С/Н1 )=р2 =0,0592

Р(С/Н2 )=1-р1 =1-0,000006=0,999994

Следовательно,

Р(С)=0,90*0,0592+0,1*0,999994=0,05328+0,0999994=0,1532794

г) Отбракованное изделие удовлетворяет стандарту. Следовательно произошла гипотеза Н1 , при условии что наступило событие С . Вероятность этого события найдем по формуле Байеса, которая служит для переоценки вероятностей гипотез после того, как стало известно, что основное событие произошло. Таким образом,

д) Найдем вероятность р3 того, что одно случайно взятое на проверку изделие удовлетворяет стандарту. Это событие противоположно событию С . Значит, р3 =1-Р(С)=1-0,1532794=0,8467206

Для нахождения вероятности тог, что из 5 изделий, взятых на проверку, только одно будет удовлетворять стандарту, воспользуемся формулой Бернулли. .

Ответ: а) ;

б) ;

в) Р(С)=0,1532794;

г) ;

д)

Задание 3

Вероятность появления события в каждом из n =112 независимых испытаний постоянна и равна р=0,1. Найти вероятность того, что событие наступит не мене 10 и не более 14 раз.

Решение:

Вероятность того, что из n=112 испытаний, событие А - появится от m1 =10 до m2 =14, вычислим по формуле:

Где

По условию вероятность появления события, равна р=0,1 .

Значит q =1-0,1=0,9

Согласно условию,

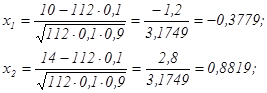
Значит,

Таким образом, вероятность наступления событии от 10 до 14 раз, равна

Ответ: вероятность наступления событии от 10 до 14 раз, равна
Задание 4

СВ Х задана функцией распределение F (х). Найти:

а) плотность распределения вероятностей;

б) математическое ожидание и дисперсию СВ Х;

в) построить графики функций F ( x ) и f ( x )

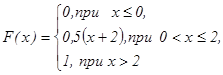
Решение:

1) Плотность распределения вероятности

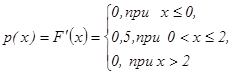
2) Вычислим числовые характеристики случайной величины Х:

Математическое ожидание М(Х) =,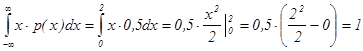

Дисперсия D ( X )=

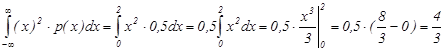
C реднее квадратическое отклонение (Х)=

3) Построим графики функций F () и p ().



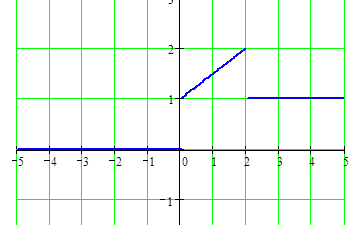
Ответ: 1)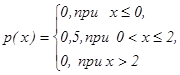

2) М(Х)=1, D ( X )=, =

Задание 5

Детали, выпускаемые цехом, по размерам распределяются по нормальному закону с параметрами: математическое ожидание а=8 см, дисперсия .

Определить:

1. вероятность того, что диаметр наудачу взятой детали имеет размеры от до ;

2. в каких границах следует ожидать размер диаметра, чтобы вероятность невыхода за эти границы была равна р=0,9934.

Решение:

1. Для вычисления вероятности того, что диаметр наудачу взятой детали имеет размеры от до , воспользуемся формулой, по которой найдем вероятность попадания нормальной СВ Х в интервал :

где Ф(х) - функция Лапласа.

Значит вероятность равна:

По таблице значений функции Лапласа находим: , .

Значит,

2. Рассмотрим событие , где . Будем считать, что вероятность этого события равна р=0,9934 :

По условию известно, что а=8 и .

Так как

Значит, по таблице значений функции Лапласа находим, что . Следовательно, .

Из неравенства , получаем

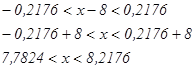
Значит, с вероятностью 0,9934 следует ожидать, что контролируемый размер детали будет заключен в границах от 7,7824 см до 8,2176 см.


Задание 6

В результате статистических наблюдений некоторой совокупности относительно количественного признака Х были получены данные, записанные в виде статистического ряда.

22 19 21 21 18 22 19 23 23 16
22 23 17 23 28 24 22 19 24 20
24 22 26 21 16 12 19 24 23 21
26 24 19 14 25 21 26 18 18 28
21 21 18 17 24 18 31 21 18 22
21 21 21 19 11 24 16 20 22 15
25 23 21 22 18 17 19 19 27 13
23 13 27 24 25 21 24 17 18 19
24 19 17 24 16 24 24 19 25 20
21 16 16 20 19

Требуется:

1. составить дискретный или интервальный ряд распределения частот и относительных частот СВ Х и построить полигон или гистограмму частот;

2. Найти эмпирическую функцию распределения случайной величины и построить ее график.

3. Вычислить числовые характеристики данного эмпирического распределения: среднее значение, дисперсию и среднее квадратическое отклонение.

4. выдвинуть гипотезу о виде распределения рассматриваемой СВ Х. Обосновать выбор вида распределения. Написать аналитическое выражение функции плотности для выбранного распределения, найти теоретические частоты и теоретическую интегральную функцию распределения.

5. приняв уровень значимости 0,05 или 0,01, по критерию согласия Пирсона проверить гипотезу о виде распределения;

6. для подтвердившегося нормального распределения найти вероятность попадания признака в интервал

Решение:

1. Для построения интервального ряда расположим различные значения признака в порядке возрастания значений. И посчитаем частоту каждого из значений. Получаем таблицу 2.

xi mx xi mx xi mx
11 1 20 4 31 1
12 1 21 14
13 2 22 8
14 1 23 7
15 1 24 13
16 6 25 4
17 5 26 3
18 8 27 2
19 12 28 2

Таким образом, видим, что xmin =11; xmax =31. Разобьем множество значений выборки на интервалы.

Найдем длину интервала:

Длина каждого интервала будет равна:

Таким образом, получаем вариационный ряд:

интервал середина интервала, xi частота, mi
11 15 13 6
15 19 17 31
19 23 21 33
23 27 25 22
27 31 29 3
95

2. Строим гистограмму и полигон частостей случайной величины.

а) Для построения полигона частот на оси абсцисс откладываем варианты хi (середины данных интервалов), а на оси ординат - соответствующие им частоты; соединив точки (xi ;mx ) получим искомый полигон частот.

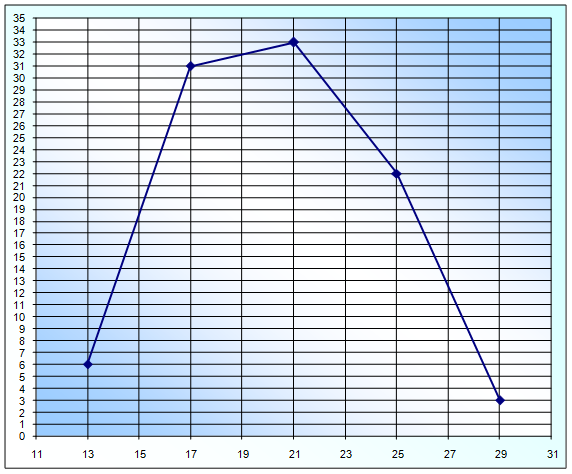
б) Для построения гистограммы частот, на оси абсцисс откладываем заданные интервалы длины h=4. Проведем над этими интервалами отрезки, параллельные оси абсцисс и находящиеся на расстояниях, равных соответствующим частотам.



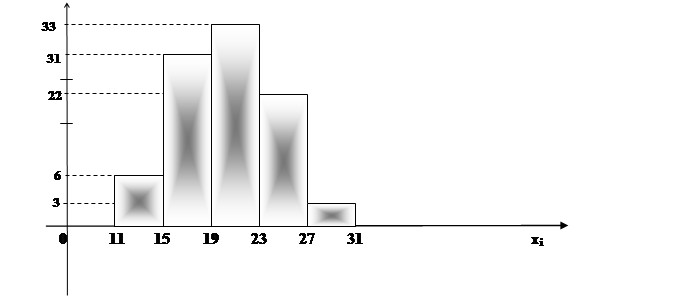3. Найдем эмпирическую функцию распределения СВ и построим ее график.

Для построения эмпирической функции распределения F* воспользуемся округлением, то есть снова возьмем середины интервалов.

При значениях аргумента, лежащих левее середины первого интервала, то есть при .

При значениях х , заключенных в интервале , .

При значениях х , заключенных в интервале ,

При значениях х , заключенных в интервале ,

При значениях х , заключенных в интервале ,

При значениях х , заключенных в интервале ,

Таким образом, получаем значения и график эмпирической функции распределения:



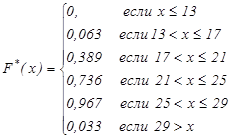
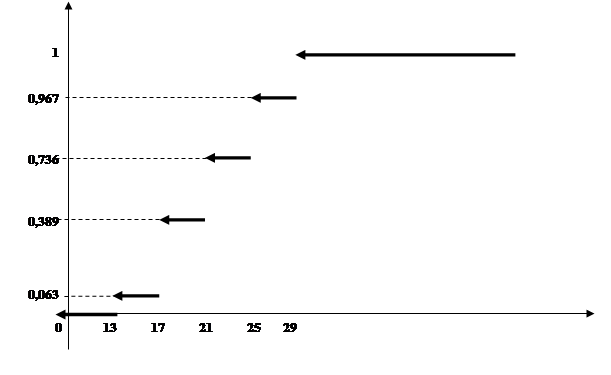4. Вычислим основные числовые характеристики данного эмпирического распределения:

Для упрощения расчетов составим таблицу:

интервал середина интервала, xi частота, mi xi mi xi 2 mi
11 15 13 6 78 1014
15 19 17 31 527 8959
19 23 21 33 693 14553
23 27 25 22 550 13750
27 31 29 3 87 2523
95 1935 40799

Таким образом,

выборочная средняя равна:

выборочная дисперсия:

выборочное среднее квадратическое отклонение:

Найдем точечные оценки параметров нормального распределения.

Точечной оценкой математического ожидания является выборочная средняя:

Точечной несмещенной оценкой дисперсии является несмещенная выборочная дисперсия:

тогда

Гипотетическая функция плотности соответствующего нормального распределения имеет вид: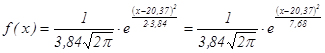

Функция распределения имеет вид: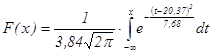

5. Проверим гипотезу о том, что данные получены из нормально распределенной генеральной совокупности с уровнем значимости a=0,01.

Составим расчетную таблицу.

интервал

середина

интервала,

xi

частота,

mi

pi ni =npi mi -ni (mi -ni )2 (mi -ni )2 /ni
11 15 13 6 -1,40 -0,500 -0,419 0,081 7,676 -1,676 2,808976 0,365943
15 19 17 31 -1,40 -0,36 -0,419 -0,141 0,279 26,467 4,533 20,548089 0,776366
19 23 21 33 -0,36 0,69 -0,141 0,255 0,396 37,5725 -4,5725 20,90775625 0,556464
23 27 25 22 0,69 1,73 0,255 0,458 0,203 19,3135 2,6865 7,21728225 0,373691
27 31 29 3 1,73 0,458 0,500 0,042 3,971 -0,971 0,942841 0,237432
95 1,000 95 2,309896

Где 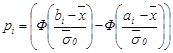. Таким образом .

По таблице критических точек распределения , по уровню значимости и числу степеней свободы находим критическую точку правосторонней критической области .

Так как - гипотезу о нормальном распределении генеральной совокупности принимаем.

Теперь для отыскания вероятности попадания признака Х в интервал
(20,37-5;20,37+3)=(15,37;23,37) воспользуемся формулой:

где Ф(х) - функция Лапласа.

У нас


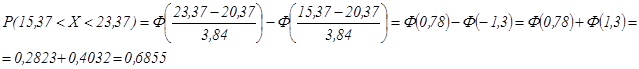
Задание 7

Приводятся результаты наблюдений (х i ; yi ) над двумерной СВ (Х,У). Используя эти экспериментальные данные, необходимо:

1) определить числовые характеристики выборки ;

2) условные средние значения величин Х и Y ;

3) коэффициент корреляции;

4) параметры эмпирической линейной функции регрессии Y на Х и X на Y и построить их графики;

5) При уровне значимости =0,05 проверить адекватность линейной регрессии исходным данным.

6) написать выборочные уравнения прямых линий регрессии у на х и х на у;

7) вычислить коэффициент корреляции и проверить гипотезу о значимости коэффициента линейной корре ляции при =0,01;

5 9 13 17 21 25 nу
3 3 3
8 6 7 2 15
13 4 10 25 39
18 8 7 4 19
23 5 2 7
28 3 1 1 2 7
nх 3 18 20 3 7 7 5 90

Решение:

Для всех вычислений, составим таблицу:

5 9 13 17 21 25 nх nх x nх x2
3 3 3 9 27
8 6 7 2 15 120 960
13 4 10 25 39 507 6591
18 8 7 4 19 342 6156
23 5 2 7 161 3703
28 3 1 1 2 7 196 5488
ny 3 18 20 37 7 5 90 1335 22925
ny y 15 162 260 629 147 125 1338
ny y2 75 1458 3380 10693 3087 3125 21818
X i Y j m xy
0 0 0 0 0 225
0 0 0 816 1176 400
0 468 1690 5525 0 0
0 1296 1638 1224 0 0
0 1035 598 0 0 0
420 252 364 952 0 0
18079

1) Найдем средние, дисперсии, исправленные дисперсии, среднеквадратические отклонения:

Найдем выборочные средние

Найдем выборочные дисперсии

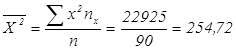
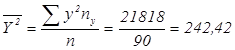
Выборочные среднеквадратические отклонения

2) Найдем условные средние значения величин Х и Y .

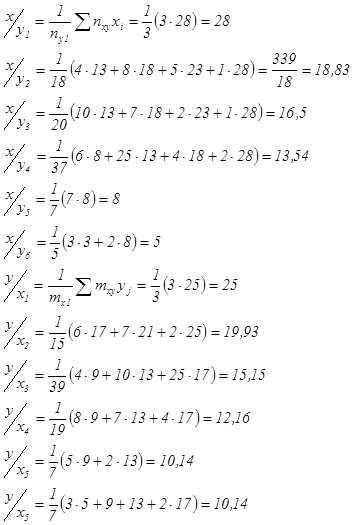
Оформим полученные данные в таблице:

yj 3 8 13 18 23 28
28 18.83 16.5 13.54 8 5
х i 5 9 13 17 21 25
25 19.93 15.15 12.16 10.14 10.14

3) Найдем коэффициент корреляции;

Найдем коэффициент корреляции:

4) Проверим значимость коэффициента корреляции на уровне a =0,01

Вычислим статистику .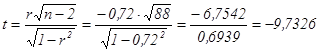

По статистическим таблицам найдем квантиль распределения Стьюдента с
n -2=88 степенями свободы и заданной надежностью a =0,01 – . Так как , то значение коэффициента корреляции считаем значимым с заданным уровнем надежности.

6) Построим корреляционные поля и по характеру расположения точек на нем сделать вывод о типе линии регрессионной зависимости между величинами Х и Y

Отметим точки и на декартовых системах координат, для этого воспользуемся таблицами, полученными в пункте 2).

1. корреляционное поле Yна X.

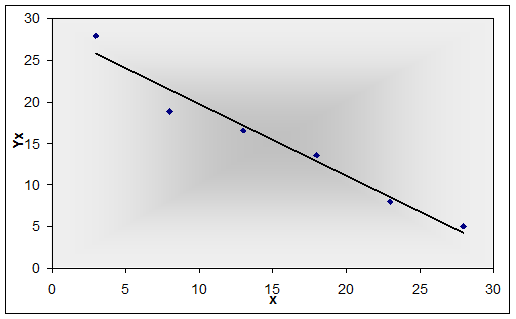
2. корреляционное поле Х на Y.

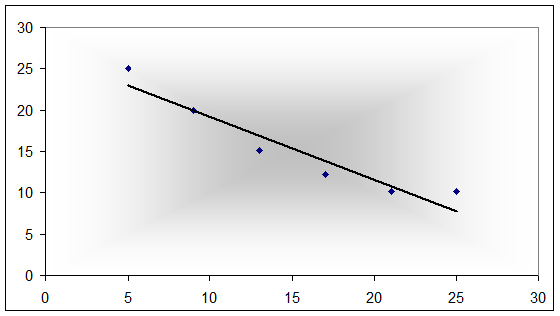
Судя по корреляционным полям, в нашем случае имеется линейная регрессионная зависимость

7) Параметры эмпирической линейной функции регрессии Y на Х и X на Y и построить их графики

Найдем коэффициенты линейной регрессии Y на Х

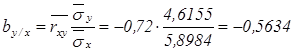
Значит уравнение регрессии Y на Х имеет вид:

, то есть или

, то есть

Найдем коэффициенты линейной регрессии Х на Y

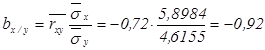
Значит уравнение регрессии Y на Х имеет вид:

, то есть или

, то есть

Построим прямые регрессий

1. Yна X

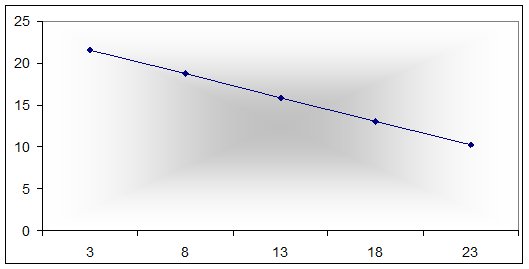
2. Х на Y

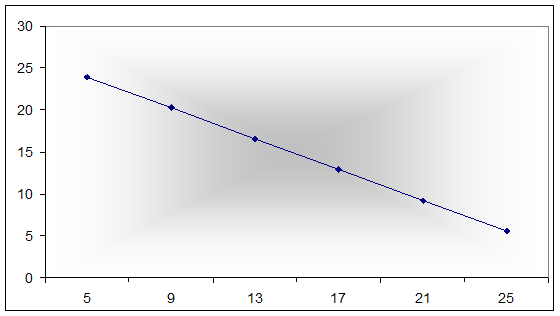
8) При уровне значимости =0,05 проверить адекватность линейной регрессии исходным данным.

Составим вспомогательную таблицу.

х 3 8 13 18 23 28
у теоретическое 28 18,83 16,5 13,54 8 5
y – эмпирические (на прямой) 21,535 18,718 15,901 13,084 10,267 7,45
-6,465 -0,112 -0,599 -0,456 2,267 2,45

Аналогично для уравнения регрессии Xна Y.

у 5 9 13 17 21 25
х теоретическое 25 19,93 15,15 12,16 10,14 10,14
х – эмпирические (на прямой) 23,9104 20,2304 16,5504 12,8704 9,1904 5,5104
-1,0896 0,3004 1,4004 0,7104 -0,9496 -4,6296

Сравнение показывает, что значения теоретических и эмпирических данных очень близки. Значит все значения корректны.


Литература

1. Белько И.В., Кузьмич К.К. Высшая математика для экономистов: Экспресс-курс. - М.: Новое знание, 2002

2. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. - М.: Высшая школа, 1988

3. Гмурман В.Е. Теория вероятностей и математическая статистика. - М.: Высшая школа, 1987

4. Гусак А.А. Бричикова Е.А. Теория вероятностей. Справочное пособие к решению задач. / Изд. 2-е, - Мн.: «Тетрасистем», 2000

Скачать архив с текстом документа