«Теория вероятностей и математическая статистика»

СОДЕРЖАНИЕ: «Теория вероятностей и математическая статистика» в школе: Методические рекомендации/ Государственное образовательное учреждение дополнительного профессионального образования «Институт повышения квалификации и переподготовки работников образования Курганской области». – Курган, 2007. 37 с

Институт повышения квалификации и переподготовки

работников образования

ПРЕПОДАВАНИЕ КУРСА

«ТЕОРИЯ ВЕРОЯТНОСТЕЙ И

МАТЕМАТИЧЕСКАЯ СТАТИСТИКА»

В ШКОЛЕ

МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ

Курган 2009


Маркова Т. Н. Преподавание курса «Теория вероятностей и математическая статистика» в школе: Методические рекомендации/ Государственное образовательное учреждение дополнительного профессионального образования «Институт повышения квалификации и переподготовки работников образования Курганской области». – Курган, 2007.-37 с.

Печатается по решению редакционно-издательского совета ИПКиПРО Курганской области

Автор-составитель: Маркова Т.Н. , зав. кабинетом математики, методист ИПКиПРО Курганской области

Рецензенты: Каргапольцева Т.А., доцент кафедры ЕМО ИПКиПРО Курганской области

Фисун Л.В., зам. директора по учебно-воспитательной работе, учитель математики высшей категории МОУ «Средняя общеобразовательная школа №53» г. Кургана, Почётный работник общего образования

Настоящее методическое пособие в первую очередь нацелено на оказание методической помощи учителям математики, приступающим к преподаванию теории вероятностей и статистики. В нём подробно освещены задачи, стоящие перед курсом теории вероятностей и статистики в средней общеобразовательной школе. Обращается внимание учителя на наиболее важные вопросы курса и на связи между ними. Приведены различные варианты планирования основных тем. Даны решения и способы записи наиболее важных типовых задач, варианты самостоятельных и контрольных работ, словарь основных понятий.

СОДЕРЖАНИЕ

ВВЕДЕНИЕ………………………………………………………………………4

I. СОДЕРЖАНИЕ КУРСА «ТЕОРИЯ ВЕРОЯТНОСТЕЙ И

МАТЕМАТИЧЕСКАЯ СТАТИСТИКА» В ПРИМЕРНЫХ

ПРОГРАММАХ ПО МАТЕМАТИКЕ (2005 год)……………………………..6

II. ПРИМЕРНОЕ ПЛАНИРОВАНИЕ КУРСА «ТЕОРИЯ

ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА»……………….7

III. МЕТОДИЧЕСКИЕ УКАЗАНИЯ И РЕКОМЕНДАЦИИ…………………...8

Тема №1. Представление данных (таблицы, диаграммы) …………………….8

Тема №2. Описательная статистика и случайная изменчивость ……………9

Тема №3 . Введение в теорию вероятностей …………………………………10

Тема №4 . События и вероятности.. …………………………………………...10

Тема №5 . Элементы комбинаторики ………………………………………….15

Тема №6 . Испытания Бернулли ………………………………………………...17

Тема №7 . Геометрическая вероятность ………………………………………18

Тема №8 . Случайные величины ………………………………………………….19

Тема №9 . Закон больших чисел ………………………………………………….20

Тема №10 . Бином Ньютона, треугольник Паскаля ............................................20

IV. САМОСТОЯТЕЛЬНЫЕ И КОНТРОЛЬНЫЕ РАБОТЫ…………………..21

V. СЛОВАРЬ ТЕРМИНОВ……………………………………………………….29

VII. СПИСОК ОСНОВНОЙ И ДОПОЛНИТЕЛЬНОЙ

ЛИТЕРАТУРЫ ПО КУРСУ «ТЕОРИЯ ВЕРОЯТНОСТЕЙ

И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА»………………………………….36

ВВЕДЕНИЕ

Теория вероятностей – это математическая наука о случайном и закономерностях случайного. В школьном курсе математики и других естественных наук господствовала только одна идея – о существовании жестких связей между явлениями и событиями. Эти связи представлены в форме законов физики, химии, математики; даже в курсе истории нет места случайности: он построен так, что все события предопределены и закономерны.

Но окружающий нас мир полон случайностей. Это землетрясения, ураганы, подъёмы и спады экономического развития, войны, болезни, случайные встречи и так далее. Теория вероятностей в средней школе – это признание обществом необходимости формирования современного мировоззрения, для которого одинаково важны представления о жёстких связях, и о случайном. Необходимо научиться измерять случайность числом, вычислять шансы различных событий. Без знания понятий и методов теории вероятностей и статистики невозможна организация эффективного конкурентоспособного производства, внедрение новых лекарств и методов лечения в медицине, обеспечение страховой защиты граждан от непредвиденных обстоятельств, проведение обоснованной социальной политики.

Теория вероятностей как наука начала складываться в XVII веке. Источником задач для неё служили азартные игры. В частности, игра в кости, которая тогда была распространена в Западной Европе. В этих задачах главное – выбор равновозможных элементарных событий. Одновременно с развитием теории вероятностей стала развиваться статистика. К XVII веку относятся и первые научные применения статистики в демографии и страховании, идеи о случайных ошибках в измерениях.

Теория вероятностей и статистика долгое время развивались как естественные науки, хотя и с большой математической составляющей. В отрасль математики теория вероятностей превратилась только в XX веке. На аксиоматическую основу её поставил наш великий соотечественник А.Н. Колмогоров. До него некоторые сложные понятия теории вероятностей не были полностью изучены. В школьном курсе мы не касаемся аксиоматики Колмогорова, но пользуемся введёнными им и общепринятыми сейчас понятиями: случайный эксперимент, элементарное событие и так далее.

Теория вероятностей и математическая статистика сформировались в научные дисциплины позже большинства других разделов математики. Однако осознание важности этих разделов математики в самых различных областях человеческой деятельности в середине прошлого века поставило во многих развитых странах вопрос о включении элементов этих дисциплин в школьную программу. В России этот вопрос начал обсуждаться ещё раньше. Ещё в 1914 году он рассматривался на заседании секции математики Российской академии наук, рекомендовавшей включение элементов теории вероятности и статистики в школьные программы.

В настоящее время теория вероятности входит в качестве обязательной дисциплины в учебные планы подготовки специалистов практически всех естественно – научных, технических и гуманитарных дисциплин в высших учебных заведениях. Элементы логики, комбинаторики, статистики и теории вероятностей становятся обязательным компонентом школьного образования, усиливающим его прикладное и практическое значение. Этот материал необходим, прежде всего, для формирования функциональной грамотности – умений воспринимать и анализировать информацию, представленную в различных формах, понимать вероятностный характер многих реальных зависимостей, производить простейшие вероятностные расчеты. Изучение основ комбинаторики позволит учащемуся осуществлять рассмотрение случаев, перебор и подсчет числа вариантов, в том числе в простейших прикладных задачах. При изучении статистики и теории вероятностей обогащаются представления о современной картине мира и методах его исследования, формируется понимание роли статистики как источника социально значимой информации и закладываются основы вероятностного мышления.

Настоящее методическое пособие в первую очередь нацелено на оказание методической помощи учителям математики, приступающим к преподаванию теории вероятностей и статистики.

В 2003-2004 гг. были изданы специальные дополнения к учебни­кам математики для 7-9 классов, в которых изложен теоретический материал и приводится большое количество задач и упражнений по элементам статистики, комбинаторики и теории вероятностей. Материал по данному курсу включён уже в некоторые учебники математики. Но в каждом из них отражён авторский подход к отбору материала и последовательности изложения тем.

При разработке общего подхода к преподаванию статистики и теории вероятностей в школе следует руководствоваться следующими положениями:

· дать законченное элементарное представление о теории вероятностей и статистики и их тесной взаимосвязи;

· подчёркивать тесную связь этих разделов математики с окружающим миром, как на стадии введения математических понятий, так и на стадии использования полученных результатов;

· избегать излишнего формализма;

· избегать утративших свою актуальность для общества примеров и задач, в том числе задач из азартных игр;

· иллюстрировать материал яркими, доступными и запоминающимися примерами.

I . СОДЕРЖАНИЕ КУРСА «ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯ СТАТИСИКА» В ПРИМЕРНЫХ ПРОГРАММАХ ПО МАТЕМАТИКЕ (2005 год)

ПРИМЕРНАЯ ПРОГРАММА ОСНОВНОГО ОБЩЕГО ОБРАЗОВАНИЯ

ЭЛЕМЕНТЫ ЛОГИКИ, КОМБИНАТОРИКИ, СТАТИСТИКИ И ТЕОРИИ ВЕРОЯТНОСТЕЙ (45 ч)

Доказательство . Определения, доказательства, аксиомы и теоремы; следствия. Необходимые и достаточные условия. Контрпример. Доказательство от противного. Прямая и обратная теоремы.

Понятие об аксиоматике и аксиоматическом построении геометрии. Пятый постулат Эвклида и его история.

Множества и комбинаторика. Множество. Элемент множества, подмножество. Объединение и пересечение множеств. Диаграммы Эйлера.

Примеры решения комбинаторных задач: перебор вариантов, правило умножения.

Статистические данные. Представление данных в виде таблиц, диаграмм, графиков. Средние результатов измерений. Понятие о статистическом выводе на основе выборки.

Понятие и примеры случайных событий.

Вероятность . Частота события, вероятность. Равновозможные события и подсчет их вероятности. Представление о геометрической вероятности.

ПРИМЕРНАЯ ПРОГРАММА СРЕДНЕГО (ПОЛНОГО) ОБЩЕГО ОБРАЗОВАНИЯ

БАЗОВЫЙ УРОВЕНЬ

ЭЛЕМЕНТЫ КОМБИНАТОРИКИ, СТАТИСТИКИ И ТЕОРИИ ВЕРОЯТНОСТЕЙ

(20 час)

Табличное и графическое представление данных. Числовые характеристики рядов данных .

Поочередный и одновременный выбор нескольких элементов из конечного множества. Формулы числа перестановок, сочетаний, размещений. Решение комбинаторных задач. Формула бинома Ньютона. Свойства биномиальных коэффициентов. Треугольник Паскаля.

Элементарные и сложные события. Рассмотрение случаев и вероятность суммы несовместных событий, вероятность противоположного события. Понятие о независимости событий. Вероятность и статистическая частота наступления события. Решение практических задач с применением вероятностных методов.

БАЗОВЫЙ УРОВЕНЬ ДЛЯ ПРОФИЛЕЙ ГУМАНИТАРНОЙ НАПРАВЛЕННОСТИ

ЭЛЕМЕНТЫ КОМБИНАТОРИКИ, СТАТИСТИКИ И ТЕОРИИ ВЕРОЯТНОСТЕЙ (25 час)

Табличное и графическое представление данных. Числовые характеристики рядов данных .

Поочередный и одновременный выбор нескольких элементов из конечного множества. Формулы числа перестановок, сочетаний, размещений. Решение комбинаторных задач. Формула бинома Ньютона. Свойства биномиальных коэффициентов. Треугольник Паскаля.

Элементарные и сложные события. Рассмотрение случаев и вероятность суммы несовместных событий, вероятность противоположного события. Понятие о независимости событий. Вероятность и статистическая частота наступления события . Решение практических задач с применением вероятностных методов.

От азартных игр к теории вероятностей. Ферма и Паскаль.

ПРОФИЛЬНЫЙ УРОВЕНЬ

ЭЛЕМЕНТЫ КОМБИНАТОРИКИ, СТАТИСТИКИ И ТЕОРИИ ВЕРОЯТНОСТЕЙ (20 ч)

Табличное и графическое представление данных. Числовые характеристики рядов данных.

Поочередный и одновременный выбор нескольких элементов из конечного множества. Формулы числа перестановок, сочетаний, размещений. Решение комбинаторных задач. Формула бинома Ньютона. Свойства биномиальных коэффициентов. Треугольник Паскаля.

Элементарные и сложные события. Рассмотрение случаев и вероятность суммы несовместных событий, вероятность противоположного события. Понятие о независимости событий. Вероятность и статистическая частота наступления события.

II . ПРИМЕРНОЕ ПЛАНИРОВАНИЕ КУРСА «ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА»

Поэтапное введение и апробация теории вероятностей и статистики проходит с 2003 года. Темы этого курса вводятся в 7 классе, исходя из трёхгодичного планирования по 12-15 часов в год. В 8 класс курс вводится, исходя из двухгодичного планирования (18 часов в 8 классе и 9 или 17 часов в 9 классе). Кроме того, в сокращённом варианте темы вводятся в программу 10-11 классов. Обзорно часть тем можно включать в программу 9 класса. Несмотря на то, что дополнения к учебникам по данной теме написаны в соответствии с образовательным стандартом для основной школы, различия между ними очень велики – и по отбору теоретического материала, и по последовательности рассмотрения изучаемых вопросов, и по характеру изложения, и по подбору задач. С учётом этого приводятся различные варианты планирования курса, независимо от учебного пособия по которому ведётся работа. Эти примерные варианты планирования помогут учителям при составлении своих учебных планов по курсу теории вероятностей и статистики, а также сориентироваться в распределении часов по основным темам.

Вариант А . 7-9 класс (три года).Предполагает изучение данного раздела в объёме, достаточном для выбора естественно-научного, социально-экономического и физико-математического профиля.

Вариант В. 7-9 класс (три года). Сокращённый вариант. Разделы, выходящие за рамки стандарта 2004 года даются обзорно или не рассматриваются.

Вариант С. 8-9 класс (два года). Сокращённый вариант. Разделы, выходящие за рамки стандарта 2004 года даются обзорно или не рассматриваются.

Вариант D . 9 класс (один год). Обзорный курс. Рекомендуется для предпрофильной подготовки школьников, ранее не изучавших данный раздел, и планирующих выбрать социально-экономический профиль.

Вариант Е. 10-11 класс. Предназначен для школьников, начинающих изучать данный материал в 10-11 классе и выбравших естественно-научный или социально-экономический профиль.

Элементы логики рассматриваются, как правило, на уроках геометрии. Из 45 часов, отведённых на изучение всей темы, целесообразно 5-7 часов посвятить изучению элементов логики, а остальные часы распределить так как показано в таблице.

№

п\п

Тема курса

7-9 класс

8-9 класс

9 класс

10-11 класс

А

В

С

D

Е

1.

Представление данных (таблицы, диаграммы)

4(7)

3(7)

3(8)

2

1(10)

2.

Описательная статистика и случайная изменчивость

5(7)

5(7)

4(8)

2

2(10)

3.

Введение в теорию вероятностей

4(7)

4(7)

2(8)

2

-

4.

События и вероятности

5(8)

5(8)

4(8)

4

4(10)

5.

Элементы комбинаторики

5(8)

5(8)

4(8)

2

3(10)

6.

Испытания Бернулли

4(8)

4(9)

4(9)

3

3(10)

7.

Геометрическая вероятность

2(9)

1(9)

1(9)

-

-

8.

Случайные величины

4(9)

3(9)

3(9)

2

3(11)

9.

Закон больших чисел

2(9)

2(9)

2(9)

1

2(11)

10.

Бином Ньютона, треугольник Паскаля

3(9)

-

-

-

2(11)

Итого:

38

33

27

18

20

III . МЕТОДИЧЕСКИЕ УКАЗАНИЯ И РЕКОМЕНДАЦИИ

Тема №1. Представление данных (таблицы, диаграммы)

Основная идея. Таблицы применяются для упорядочивания большого количества числовых данных. При этом таблицы особенно удобны, когда имеется несколько характеристик одного объекта. Например, у одного поезда есть множество интересных пассажиру свойств – номер, категория, регулярность движения, время отправления и время прибытия. Диаграммы бывают разных видов. Они используются для наглядного представления данных. При этом диаграмма может не обеспечивать высокую точность, зато она позволяет быстро на глаз сравнивать величины между собой. Диаграмма лучше запоминается, чем таблица. Рассматриваются диаграммы трёх видов – столбчатая, круговая и диаграмма рассеивания.

Результаты обучения. В результате изучения данной темы обучающийся должен:

· уверенно искать нужную информацию в таблице;

· выполнять элементарные вычисления по табличным данным и заносить результаты в соответствующие ячейки таблицы;

· уметь производить подсчёт предметов в длинном списке и составлять таблицу результатов подсчёта;

· уметь составлять таблицы с результатами измерений;

· уметь строить столбчатые и круговые диаграммы по имеющимся данным;

· понимать, что столбчатые диаграммы удобнее применять для изображения абсолютных величин, а круговые для изображения долей целого;

· понимать, что такое диаграмма рассеивания и уметь выдвигать гипотезы о наличии или отсутствии связи между показанными на диаграмме рассеивания величинами.

Тема №2. Описательная статистика и случайная изменчивость

Основная идея. Познакомить учащихся с тем, как с помощью всего нескольких чисел можно составить представление о больших наборах чисел, описать их в среднем. В этом и заключается одна из главных задач описательной статистики. Дать представление о том, что точных величин в окружающем нас мире мало, что реальность полна изменчивости в самых разных проявлениях. Одновременно закладывается важная мысль, что в случайной изменчивости тоже могут быть свои закономерности. Отдельное внимание уделяется точности измерений (насколько точны должны быть измерения тех или иных изменчивых величин).

Результаты обучения. В результате изучения данной темы обучающийся должен:

· знать, что такое среднее значение (среднее арифметическое) и уметь вычислять его;

· знать, что среднее арифметическое - не единственная мера положения набора чисел на числовой прямой, что существуют и другие;

· уметь объяснять, что такое медиана числового набора и уметь вычислять её для несложных наборов;

· понимать, что такое наибольшее и наименьшее значение набора чисел, его размах и уметь их вычислять;

· знать, что такое отклонение от среднего арифметического и дисперсия и уметь вычислять их на коротких наборах;

· понимать, что большинство реальных физических величин подвержено случайной изменчивости;

· уметь приводить примеры таких величин: напряжение в бытовой сети, параметры продукции при массовом производстве, рост человека и т.п.;

· уметь указывать различные факторы, приводящие к изменчивости различных величин и понимать, что этих факторов, как правило, много;

· уметь указывать приблизительно меру точности измерения масс различных предметов и обосновать свою точку зрения.

Тема №3 . Введение в теорию вероятностей.

Основная идея. Качественное описание случайных событий и их вероятностей. Дать представление о случайном опыте, о том, что такое вероятность и частота наступления события, о том, как они связаны.

Результаты обучения. В результате изучения данных тем обучающийся должен:

· уметь приводить примеры случайных событий;

· понимать, что вероятность – числовая мера правдоподобия события, что вероятность – число, заключённое в пределах от 0 до 1;

· верно понимать фразы вида «вероятность события равна 0,3»;

· знать, что такое частота события, что при увеличении числа опытов частота приближается к вероятности;

· иметь представление о математической монете и игральной кости;

Тема №4 . События и вероятности.

Основная идея. Развивать представление о случайном событии, приписывая каждому из них некоторую вероятность – численное выражение шансов на осуществление этого события, возможность прогнозирования событий на основе знания вероятностей. Осуществить переход от качественного описания событий к их математическому описанию. Ввести понятия: элементарные события, равновозможности, равновероятности и вероятности элементарных событий. Напомнить, что

· любое случайное событие требует условий, в которых оно может осуществиться;

· случайный опыт порождает случайные события, событие без опыта невозможно;

· в результате опыта наступает одно и только одно событие.

Решение каждой задачи следует начинать с описания множества элементарных событий и благоприятствующих элементарных событий.

Результаты обучения. В результате изучения данной темы обучающийся должен:

· иметь представление об элементарном событии как о простейшем событии, которое нельзя составить из более простых событий;

· знать, что любой случайный опыт оканчивается одним и только одним элементарным событием;

· уметь вводить обозначения для элементарных событий простого опыта;

· уметь записать элементарные события простого опыта, например, бросание одной или двух игральных костей, бросании монеты и т.п.

· распознавать опыты, в которых элементарные события считаются равновозможными;

· знать, что сумма вероятностей всех элементарных событий равна единице;

· вычислить вероятность элементарного события в опыте с равновозможными событиями;

· знать, что такое противоположные события и уметь находить вероятность одного из них по вероятности другого;

· понимать, что такое объединение и пересечение событий;

· понимать, что такое несовместные события;

· знать и уметь применять формулу сложения вероятностей для несовместных событий (минимум); желательно знание формулы сложения для произвольных событий;

· знать, что такое независимые события (и не путать их с несовместными);

· уметь применять формулу умножения вероятностей независимых событий.

Практическое задание

Цель исследования. Установить, можно ли считать первую пришедшую в голову цифру от 0 до 9 случайной.

Ход исследования. В классе должно присутствовать по крайней мере 20
учащихся. Каждый ученик, приготовив заранее листок бумаги и ручку, по
команде учителя, не задумываясь, быстро пишет на листке четыре первые
пришедшие ему в голову цифры от 0 до 9.

Затем все листки сдаются учителю. Учитель сам или с помощником подсчитывает, сколько раз написана каждая из цифр. Полученные данные заносятся в таблицу.

Анализ результатов. Если выбор носит чисто случайный характер, то все цифры должны встретиться примерно одинаковое количество раз. Например,

Цифра

0

1

2

3

4

5

6

7

8

9

Сколько раз эта цифра написана

если в классе 20 учеников, то всего получено 80 цифр. Тогда каждая цифра должна встречаться примерно 8 раз. Если цифра встречается менее 4 раз, то её можно считать «редкой». Если цифра встретилась более 12 раз, то такая цифра «частая». Пользуясь построенной таблицей, ответьте на вопросы.

а) Есть ли в таблице «частые» и «редкие» цифры?

б) Попробуйте объяснить, какие исторические явления и культурные традиции связаны с числами 3 и 7. А с числом 8?

Сделайте вывод о том, можно ли считать первую пришедшую и голову цифру случайной.

Примеры решения задач. Приведем несколько примеров решения типовых задач.

1. В ящике четыре детали: две исправные детали а и Ъ и две бра­кованные детали с и d . Из ящика наугад извлекают по одной детали, пока не обнаружат все бракованные. Элементарные события этого опыта будем записывать в виде последовательности букв. Например, ab с d , cad и так далее.

а) Является ли cdab элементарным событием в этом опыте?

б) Какими буквами может заканчиваться запись элементарного события?

в) Выпишите все элементарные события этого опыта.

г) Сколько различных элементарных событий записывается тремя бук­вами?

Решение.

а), б) Эксперимент заканчивается извлечением бракованной детали. По­этому запись любого элементарного события оканчивается либо буквой с, либо буквой d . Следовательно, cdab элементарным событием не является.

в) Все элементарные события:

cd , dc , acd , adc , b с d , bd с, dac , cad , dbc , cbd , ab с d , abdc , bacd , bad с, cabd , cbad , dabc , dbac , acbd , b с ad , adb с, bdac .

г) При решении предыдущего параграфа выписаны все элементарные
события. Из них 8 событий записывается тремя буквами.

2. При подбрасывании монеты будем обозначать буквой О выпадение орла, и буквой Р выпадение «решки».

а) Подбросим монету два раза. Появление двух орлов записывается
как 00. Это одно из элементарных событий этого опыта. Выпишите все
элементарные события этого опыта.

б) Подбросим монету три раза. Выпишите все элементарные события
этого опыта.

в) Во сколько раз больше число элементарных событий при трех броса­
ниях монеты, чем при двух бросаниях монеты?

Решение.

а) 00, РО, OP, PP. Здесь встречается типичная ошибка: отождествляются
элементарные события РО и ОР. Это разные события!

б) 000, OOP, ОРР, ОРО, POO, POP, РРО, РРР.

в) при двух бросаниях 4 элементарных события, при 3 бросаниях — 8
событий, то есть в 2 раза больше.

3 . а). Случайный опыт может закончиться одним из трех элементарных событий: a , b или с. Чему равна вероятность элементарного события с, если

P ( a ) = 1/2, P ( B )=1/3 ?

Решение. Сумма вероятностей всех элементарных событий равна 1: Р{а) + Р(Ь) + Р(с) = 1, откуда Р(с) = 1 - (1/2 + 1/3) = 1/6.

4. Три первоклассника по очереди покупают воздушные шарики. Каждый из них покупает шарик одного из двух цветов: зеленого (3) или синего (С). Выпишите элементарные события этого эксперимента. Считая, что все они равновозможны, найдите вероятность каждого из них.

Решение. Какова бы ни была очередность первоклассников, каждый из них может выбрать любой из шариков. Элементарные события:

333, ЗЗС, ЗСЗ, ЗСС, СЗЗ, ССЗ, СЗС, ССС.

Всего 8 событий, поэтому вероятность каждого равна 1/8.

8

5 . Симметричную монету бросают трижды. Выпадение орла при каждом бросании обозначим через О, а выпадение решки — через Р. Выпи­шите элементарные события, благоприятствующие событию «выпал ровно один орел».

Решение. Указанному событию благоприятствуют те элементарные собы­тия, в записи которых присутствует ровно одна буква О. Это элементарные события ОРР, POP и РРО.

Анализ и решение данных задач можно осуществлять по следующей схеме:

1. Уясните, в чем состоит рассматриваемое в задаче испытание.

2. Обозначьте буквами события, рассматриваемые в условии
 задачи.

3. С помощью введенных обозначений выразите событие, вероят­ ность наступления которого необходимо найти.

4. Если требуется найти вероятность суммы событий, выясните,
совместны или несовместны рассматриваемые события. Если же
 требуется найти вероятность произведения событий, выясните,
 зависимы или независимы рассматриваемые события.

5. Выберите соответствующую условию задачи формулу и вы­
полните необходимые вычисления.

6. Иван Иванович отправился охотиться на медведей и зайцев и оценивает свои перспективы следующим образом:

— Один шанс из четырех за то, что попадется только заяц; один к десяти за то, что подстрелю только медведя; один к сорока,— что будет и медведь, и заяц.

Найдите вероятность того, что не видать Ивану Ивановичу в качестве охотничьего трофея:

а) ни одного зайца; б) ни одного медведя; в) ни медведя, ни зайца.

Решение. Введем обозначения для событий: А —«ни одного зайца», В — «ни одного медведя» и С —«ни медведя, ни зайца».

Элементарными событиями опыта являются следующие события: «толь­ко заяц» (а), «только медведь» (Ь), «и заяц, и медведь» (с) и «ни зайца, ни медведя» (d). Из условия задачи находим: Р(a) = 1/4, Р(b) = 1/10 и Р(с) = 1/40.

Тогда P(d) = 1-(1/4+ 1/10 + 1/40) = 5/8.

Событию А благоприятствуют элементарные события b и d.

Поэтому Р(А) = Р(Ь) + P(d) = 1/10 + 5/8 = 29/40.

Аналогично находятся вероятности остальных событий.

7. В коробке лежат 24 одинаковые авторучки. Из них 13 красные, 5 зеленые, остальные — синие. Продавец наудачу достает одну авторучку. Найдите вероятности событий:

а) «извлеченная ручка красная»;

б) «извлеченная ручка не зеленая».

Решение. Элементарными событиями в описанном опыте являются со­
бытия К, 3 и С.

а) Вероятность элементарного события К равна 13/24.

б) Вероятность элементарного события 3 равна 5/24. Синих ручек 6,
следовательно, вероятность элементарного события С равна 6/24.

Событию А «извлеченная ручка не зеленая» благоприятствуют элемен­тарные события К и С, поэтому Р(A) = 13/24 + 6/24 = 19/24.

8. Могут ли быть противоположными события С и D , если

а) Р(С) = 0,12; P(D) = 0,78; б) Р(С) = 0,14; P ( D ) = 0,86.

Решение, а) Р(С) + Р(D) = 0,12 + 0,78 = 0,9. Полученная сумма не равна 1, поэтому события С и D не являются противоположными.

б) P(C)+P(D) =0,14 + 0,86= 1. Полученная сумма равна 1, поэтому
события С и D могут (но не обязаны) быть противоположными.

9 . а). Бросают одну игральную кость. Событие А — «выпало четное число очков». Событие В состоит в том, что выпало число очков, кратное 3. Выпишите все элементарные события, благоприятствующие событие AUB . Найдите P(AUB).

Решение. Элементарными событиями опыта можно считать числа 1, 2, 3, 4, 5 или 6. Событию А благоприятствуют элементарные события 2, 4 и 6. Событию В благоприятствуют элементарные события 3 и 6.

Событие A U В состоит в том, что выпало либо четное, либо кратное трем число очков. Этому событию благоприятствуют 4 элементарных со­бытия 2, 3, 4 и 6. Все элементарные события равновозможны, поэтому P(AUB) = 4/6 = 2/3.

10. Известно, что Р(А) = 0,4, Р(В) = 0,8 и Р(АВ) = 0,2. Докажите, что событие A UB является достоверным.

Решение. Применим формулу сложения вероятностей:

P(AUB) = Р(А)+Р(B)-Р(AB) = 0,4 + 0,8 – 0,2 =1

Следовательно, событие AUB является достоверным. Доказательство окон­чено.

11. а). Бросают одну игральную кость. Событие А — «выпало четное число очков». Являются ли независимыми события А и В, если событие В состоит в том, что выпало число очков, кратное 3.

1

Решение. Элементарными событиями этого опыта являются числа 1, 2, 3, 4, 5, 6. Событию А благоприятствует 3 элементарных события 2, 4 и 6, поэтому

Р(А) = 1/2. Событию В благоприятствует 2 элементарных события 3 и 6, поэтому P(B) = 1/3. Событие А В состоит в том, что выпало число 6. Поэтому Р(АВ) = 1/6.

Нужно проверить равенство Р(АВ) = Р(А) • Р(В).

Подставим в это равенство найденные значения: 1/6 = 1/2 • 1/3. Равенство верно. Следовательно, события А и В независимы.

12. В двух коробках лежат карандаши одинаковой величины и формы, но разного цвета. В первой коробке 4 красных и 6 черных, а во второй 3 красных, 5 синих и 2 черных. Из обеих коробок вынимается наугад по одному карандашу. Какова вероят­ность того, Что оба карандаша окажутся красными?

Решение. Испытание состоит в том, что из каждой коробки вынимается по одному карандашу. Пусть событие А означает, что вынутый карандаш из первой коробки оказался красным, событие

В — что вынутый карандаш из второй коробки тоже красный. Тогда событие АВ означает, что оба вынутые карандаша оказались красными. Поскольку события А и В независимы, то P (АВ) = P (А) P (В). Вероятности событий А и В равны соответственно P(А) = 0,4, P(В) = 0,3. Следовательно, вероятность того, что оба карандаша оказались красными, равна P (АВ) = 0,4 • 0,3 = 0,12.

Тема №5 . Элементы комбинаторики

Основная идея. Дать учащимся различные способы описания всех возможных элементарных событий в различных типах случайного опыта. Познакомить учащихся с перестановками и факториалом числа, правилом умножения и числом сочетаний, построением треугольника Паскаля. Формулировки Комбинаторные задачи желательно формулировать на простых, понятных и запоминающихся примерах из жизни, а не в формальных терминах перестановок и сочетаний и т.п. Кроме того, полезно начинать знакомство с тем или иным комбинаторным правилом методом простого перебора и обращать внимание, что его можно использовать для поверки применяемой формулы, если перебор не велик.

Результаты обучения. В результате изучения данной темы обучающийся должен:

· уметь методом перебора находить ответы в комбинаторных задачах для небольших объёмов перебора;

· уметь вычислять число упорядоченных пар, пользуясь правилом умножения;

· уметь вычислять n!; знать факториалы натуральных чисел до 5! и уметь пользоваться таблицей факториалов до 10!;

· уметь находить число перестановок элементов произвольного конечного множества;

· уметь вычислять , пользуясь формулой =

· уметь решать простейшие задачи, в которых число благоприятствующих элементарных событий находится как число сочетаний

Примеры решения задач.

Три вида основных комбинаторных задач.

1. В соревновании участвуют 7 команд. Сколько существует вариантов распределения мест между командами?

2. В полуфинале участвовало 7 команд. Из них в финал вышли 3. Сколько различных вариантов выхода команд в финал?

3. Из 7 команд, участвующих в полуфинале, 3 команды разыграли медали: золотую, серебряную и бронзовую. Сколько различных вариантов тройки победителей существует?

Из этих задач видна общая схема их решения: имеются некоторые множества, содержащие n , из этих элементов составляются различные наборы, комбинации, которые можно различать:

· по порядку расположения элементов;

· по составу;

· по составу и порядку;

А значит и решения этих задач будут основываться на различных формулах комбинаторики:

1. Число перестановок: n •( n -1)•( n -2)•…•2•1 = n ! ;

= 7!= 5040.

2. Число сочетаний: = ;

= = 35.

3. Число размещений: = n •( n -1)•( n -2)•…•( n - k +1); = 7•6•5 = 210.

13 . На книжной полке стоят 20 книг по алгебре, 12 — по теории вероятностей, 7 — по геометрии и 25 — по литературе. Сколькими способами можно выбрать книгу по математике?

Решение. Найдем число способов, которыми можно вы­брать книгу по алгебре, или по теории вероятностей, или по геометрии. Книгу по алгебре можно выбрать 20 спосо­бами, по теории вероятностей — 12 способами и по геометрии— 7 способами. Эти выборы несовместны. Поэтому по правилу суммы находим, что выбрать книгу по математике можно N = 20+ 12 + 7 = 39 способами.

14. Сколько трехзначных чисел можно составить из цифр 1, 3, 5, если цифры в числе не повторяются?

Решение. На месте сотен поставим любую из трех цифр. После каждого такого выбора на месте десятков можно поставить любую из двух оставшихся цифр, так как цифры в числе не по­вторяются. Наконец, на месте единиц можно поставить оставшуюся одну цифру. Повторным применением правила произведения най­дем число трехзначных чисел, равное N = 3 • 2 • 1=6.

15. Сколько различных «слов», состоящих не ме­нее чем из четырех разных букв, можно образовать из букв слова ученик?

Решение. Слово ученик состоит из шести различных букв. По правилу произведения можно составить = 6 • 5 • 4 • 3 = = 360 четырехбуквенных слов, N 2 = 6 • 5 • 4 • 3 • 2 = 720 пятибуквенных и

N 3 = 654321= 720 шестибуквенных слов. По правилу суммы всего можно составить N = 360 + 720 + + 720 = 1800 слов, состоящих не менее чем из четырех букв.

16. В подразделении 5 офицеров, 10 сержантов и 50 солдат. Сколько нарядов, состоящих из 1 офицера, 2 сержантов и 3 солдат, можно составить?

Решение.=13230000.

Тема №6 . Испытания Бернулли

Основная идея. Схема испытаний Бернулли является не только относительно простой, полезной и распространённой на практике моделью однотипных повторяющихся независимых опытов с двумя возможными исходами. Она играет в теории вероятностей важную методическую роль, определяя алгоритм приближенного поиска вероятностей многих интересующих нас событий. Если учитель не сочтёт возможным касаться всех вопросов этой темы в основном курсе, а остановится только на самой схеме Бернулли, то он должен хорошо понимать, что здесь им закладывается основа для углубленного знакомства учащихся с теорией вероятностей. Сама по себе схема испытаний Бернулли объединяет целый ряд понятий и методов, введённых ранее. Это представление о множестве элементарных событий, понятие о независимости событий, правило умножения вероятностей, число сочетаний. Таким образом, эта важная

Результаты обучения. В результате изучения данной темы обучающийся должен:

· знать, что такое отдельное испытание Бернулли, что такое успех и неудача и как связаны их вероятности;

· понимать, что такое серия независимых одинаковых испытаний Бернулли. Здесь независимость понимается в обычном смысле – как отсутствие влияний одного испытания на другое;

· уметь вычислять вероятность элементарного события вида НУНУ серии из n испытаний Бернулли;

· уметь вычислять число элементарных событий, благоприятствующих ровно k успехам в серии испытаний Бернулли;

· знать формулу вероятности ровно успехов и уметь ею пользоваться.

Практикум. Для иллюстрации связи частоты и вероятности событий учитель может провести небольшой практикум в классе или предложить учащимся выполнить его дома. В 7 классе можно огра­ничиться только вычислением частоты события, не рассматривая других характеристик. Предположим, что в классе 25 человек. Каждому из них потребуется 4 обычные монеты любого достоинства. (При другом количестве учащихся в классе удобно сделать так, чтобы в сумме они бросали 100 монет). Хорошо, если у школьников будут пластиковые стаканы или пеналы и т. п. для того, чтобы из них выбрасывать монеты — это практически обеспечивает случайность результата каждого броска.

На доске должна быть заготовлена таблица

Число опытов

100

200

300

Число орлов

Частота

В тетради у каждого школьника заготовлена маленькая табличка:

Номер броска

1

2

3

Число орлов

Каждый опыт состоит в бросании одной монеты. За один раз каждый школьник бросает 4 монеты. Таким образом, все учащиеся в классе сра­зу проводят 100 опытов. Бросив монеты, школьники записывают в свою табличку число выпавших орлов и сообщают результат учителю. Общее число орлов, подсчитанное по всему классу, заносится в таблицу на доске. После этого вычисляется частота выпадения орла. После следующей серии бросков получается уже 200 экспериментов. Общее число орлов, выпавших при втором бросании, прибавляется к предыдущей сумме и заполняется второй столбец таблицы на доске. Этот процесс повторяется до тех пор, пока не будет заполнена вся таблица.

Если теперь сравнить частоты для разного числа бросков, то можно заметить, что с ростом числа бросков частота выпадения орла становится ближе к 0,5.

Тема №7 . Геометрическая вероятность

Основная идея. Познакомить учащихся с одним из возможных способов задания вероятности в специфическом классе задач. С методической точки зрения геометрическую вероятность иногда используют для формирования представления о более сложных событиях, событиях составленных из бесконечного множества элементарных событий. Однако на этом пути много сложностей, обсуждение которых в школьном курсе неуместно. Поэтому материал по этому вопросу занимает отчасти изолированное место в школьном курсе теории вероятностей и больше служит для повторения уже пройденного и закрепления навыков формализации текстовых вероятностных задач с помощью геометрических фигур. При обсуждении темы могут возникнуть некоторые трудности. Говоря о том, что элементарным событием в опыте выбора произвольной точки из фигуры является точка, учитель столкнётся с двумя проблемами. Число элементарных событий становится не только бесконечным, но и несчетным. А вероятность каждого отдельного элементарного события при этом равняется нулю. Отсюда вытекает, что вычисление вероятности события как суммы вероятностей составляющих его элементарных событий приводит к необходимости разрешения неопределённости типа «0». Геометрический способ задания вероятности событий в этом случае служит одним из возможных путей ответа на вопрос.

Результаты обучения. В результате изучения данной темы обучающийся должен:

· знать определение геометрической вероятности выбора точки из фигуры на плоскости или прямой;

· уметь решать простейшие задачи на геометрическую вероятность, зная площади фигур или умея их вычислять.

Тема №8 . Случайные величины

Основная идея. Данная тема в настоящее время не входит в образовательный стандарт, но без неё материал курса получается логически не завершённым. Значительная часть материала предыдущих тем уже подготовила учащихся к работе со случайными величинами.

Результаты обучения. В результате изучения данной темы обучающийся должен:

· уметь приводить примеры случайных величин;

· выделять на интуитивном уровне из множества различных случайных величин дискретные (с конечным или счётным множеством значений; разумеется, термин «счётное» здесь использован не для школьника»;

· понимать, что число успехов в серии из n испытаний Бернулли является случайной величиной с множеством значений 0, 1, 2, . . ., n.

· понимать, что такое распределение вероятностей случайной величины и уметь составлять таблицы распределения для случайных величин с небольшим числом возможных значений;

· знать, что такое распределение Бернулли;

· знать определение математического ожидания конечной случайной величины, понимать, что математическое ожидание является обобщением среднего арифметического значений величины;

· знать свойства математического ожидания и уметь использовать их при решении простых задач;

· знать, что важным свойством распределения случайной величины является рассеивание величины. Уметь вычислять дисперсию и стандартное отклонение;

· знать формулы математического ожидания и дисперсии числа успехов в серии испытаний Бернулли.

Тема №9 . Закон больших чисел

Основная идея. На практике вероятности многих событий и случайных величин невозможно рассчитать, их можно узнать только экспериментальным методом, и для этого требуется свойство близости частоты и вероятности. С помощью минимума математических средств мы высказываем одну из основных идей, лежащих в основе современных исследований в естествознании и социальных науках: выборочный метод обследования позволяет не только получить содержательные результаты, но и оценить их точность. При этом объём выборки не зависит от численности обследуемой совокупности (группы населения, популяции животных или партии товара). Закон больших чисел утверждает, что среднее ариметическое большого числа слу

Результаты обучения. В результате изучения данной темы обучающийся должен:

· знать, что неизвестные вероятности событий можно оценивать с помощью частоты числа успехов в схеме испытаний Бернулли;

· понимать, что при этом можно оценить точность приближения;

· понимать суть закона больших чисел.

Тема №10 . Бином Ньютона, треугольник Паскаля

Основная идея. Эти темы не имеют непосредственного отношения к курсу теории вероятностей и статистики, они опираются на более высокий уровень формализма в записи выражений. Обращаться к этим темам стоит лишь после того, когда завершено прохождение материала по статистике и теории вероятностей. В этом случае появляется возможность показать, как содержательно используется этот материал в теории вероятностей.

Результаты обучения. В результате изучения данной темы обучающийся должен:

· знать алгоритм вычисления числа сочетаний =, формулу бинома Ньютона;

· понимать смысл биномиальных коэффициентов;

· иметь представление о треугольнике Паскаля.

IV . САМОСТОЯТЕЛЬНЫЕ И КОНТРОЛЬНЫЕ РАБОТЫ

7 класс.

Самостоятельная работа 1 по теме «Таблицы»

1. В таблице представлен объем экспорта естественного газа из России в некоторые страны мира в 2001 г.

Страны

Экспорт газа из России в 2001 г., млрд. куб. м

Страны

Экспорт газа из России в 2001 г., млрд. куб. м

Литва

2,68

Швейцария

0,34

Латвия

1,46

Турция

11,12

Эстония

0,82

Финляндия

4,64

Австрия

4,91

Франция

11,15

Болгария

3.32

Чехия

7,46

Венгрия

8,10

Словакия

7,52

Италия

20,20

Югославия

1,57

Германия

32,60

Нидерланды

0,13

Польша

7,51

Греция

1,52

Румыния

2,88

По данным таблицы укажите:

а) наиболее крупных потребителей российского газа (более 10 млрд. куб. м);

б) государства, которые в 2001 г. получили менее 1 млрд. куб. м.;

в) общий объем газа, экспортированного в 2001 г. в указанные страны.

2. Участники Интернет-форума указали города, где они проживают. Полу­чился следующий список:

Москва, Смоленск, Москва, Москва, С.-Петербург, Челябинск, Назрань, Москва, Норильск, Уфа, Москва, Волгоград, С.-Петербург, Ногинск, Москва, Москва, Челябинск, Москва, С.-Петербург, С.-Петербург, Москва, Челябинск, Дмитров, Москва, Ижевск, Мурманск, Волгоград, Москва, Ярославль.

Составьте таблицу подсчета и таблицу распределения участников форума по городам.

Самостоятельная работа 2 по теме «Диаграммы»

1. В таблице даны денежные вклады граждан России в Сбербанке РФ в каж­дом месяце 1995 г.

Месяц

1

2

3

4

5

6

7

8

9

10

11

12

Вклад, млрд. руб.

550

560

560

640

640

1100

1100

1100

1630

1610

1610

2500

Постройте столбиковую диаграмму, отражающую данные таблицы. 2. На круговой диаграмме показан объем поставок российского газа в три страны СНГ в январе-августе 1995 г.

а) В какую из этих трех стран было поставлено больше всего газа в 1995 г.? В какую меньше всего?

б) С помощью транспортира и калькулятора найдите приближенно объем поставок в Беларусь, если суммарная поставка во все три страны равна 57 168,1 млрд. куб. м газа.

Самостоятельная работа 3 по теме

«Случайная изменчивость, среднее значение»

1. В сосуд с теплой водой погрузили 10 термометров. Термометры показали следующие результаты:

34,5°; 35,1°; 34,4°; 34,2°; 34,7°; 34,6°; 35,0°; 34,2°; 34,5°; 34,8°.

а) Чем может объясняться изменчивость в показаниях термометров? Назо­вите хотя бы две возможные причины.

б) Расположите полученные значения по возрастанию.

в) Найдите среднее значение температуры и размах полученного набора.

2. Пользуясь результатами задачи 1, составьте таблицу отклонений пока­заний термометров от среднего значения. Сколько показаний меньше, чем среднее? Сколько показаний больше, чем среднее?

3. Пользуясь результатами задачи 1. найдите медиану показаний термомет­ров. Сколько показаний больше и сколько показаний меньше медианы?

Самостоятельная работа 4 по теме «Разброс и дисперсия»

1. Дан набор чисел 3: 1: 5: 2; — 1; 0; 3; 4.

а) Найдите размах этого набора.

б) Найдите среднее значение, составьте таблицу квадратов отклонений от среднего.

в) Найдите дисперсию набора.

2. Даны два набора чисел: 7; 4; 9; 8 и 2; —1; 4; 3.

а) Отметьте числа обоих наборов на числовой прямой.

б) Вычислите дисперсию каждого из наборов.

в) У какого набора дисперсия больше?

Примерная контрольная работа

Вариант 1

1. В таблице представлена смета расходов при покупке продуктов питания. Заполните столбец «Стоимость».

Наименование товара

Цена за кг

Вес, кг

Стоимость

Сахарный песок

19 р.

2

Сыр

105 р.

0,4

Мука

28 р.

2

Рис

21 р.

1

Картофель

9 р.

4

Всего

2. За диктант по русскому языку учительница поставила 7 пятерок, 9 четве­рок, 8 троек и 2 двойки. Постройте столбиковую диаграмму по этим данным. Вычислите среднюю оценку.

3. Дан набор чисел 1; 3; —4; 2; 7; 5. Найдите среднее значение и медиану этого набора.

4. В таблице представлено производство автомобилей на некотором автоза­воде по годам.

Год

1997

1998

1999

2000

2001

2002

2003

Число автомобилей,

тыс.штук

84

77

81

79

85

102

113

Составьте таблицу изменения производства автомобилей по сравнению с 1997 г. в процентах.

5*. В таблице представлены среднемесячные температуры за первые 6 ме­сяцев года в Волшебной стране.

Месяцы

Январь

Февраль

Март

Апрель

Май

Июнь

Температура, °С

-9

-7

-3

5

11

15

Вычислите дисперсию температуры за эти полгода. Результат округлите до десятых.

Вариант 2

1. В таблице представлена смета расходов при покупке электротоваров. Заполните столбец «Стоимость».

Наименование товара

Цена за шт.

Кол-во

Стоимость

Лампа электрическая

5 р.

24

Выключатель

30 р.

15

Предохранитель

40 р.

4

Розетка бытовая

35 р.

10

Счетчик электроэнергии

620 р.

1

Всего

2. В понедельник и во вторник магазин продал по 5 автомобилей, в сре­ду—6, в четверг —4, в пятницу —8, а в субботу— 12 автомобилей. Вычислите среднее число автомобилей, проданных за день. Постройте по этим данным столбиковую диаграмму «число проданных автомобилей по дням».

3. Дан набор чисел 3; 6; 4; —2; 5; 8. Найдите среднее значение и медиану этого набора.

4. Таблица показывает, сколько пассажиров перевезла некоторая авиаком­пания в каждом году.

Год

1997

1998

1999

2000

2001

2002

2003

Число пассажиров,

тыс. чел.

484

375

398

467

481

407

442

Составьте таблицу изменения для числа пассажиров авиакомпании по срав­нению с 1997 г. в процентах.

5*. В таблице представлены среднемесячные температуры за 6 последних месяцев года в Тридесятом королевстве.

Месяцы

Июль

Август

Сентябрь

Октябрь

Ноябрь

Декабрь

Температура, °С

20

16

11

4

-2

-7

Вычислите дисперсию температуры за эти полгода. Результат округлите до сотых.

8 класс

Самостоятельная работа 1 по теме «Элементарные события»

1. Бросают одну игральную кость. Перечислите элементарные события, бла­гоприятствующие событию «выпало нечетное число очков»

2. Нарисуйте в тетради таблицу элементарных событий при бросании двух игральных костей. Выделите в этой таблице цветными карандашами элемен­тарные события, благоприятствующие событиям:

а) на обеих костях выпало число очков меньшее, чем 3;

б) сумма очков на двух костях равна 7;

в) произведение выпавших очков равно 12.

3. В случайном опыте всего три элементарных события a , b и с. Вероят­ности элементарных событий а и b соответственно равны 0,4 и 0,1. Найдите вероятность события, которому:

а) благоприятствует элементарное событие с;

б) благоприятствуют элементарные события а и с.

4. В шахматной коробке лежит 5 черных и 6 белых пешек. Игрок, не глядя, вынимает одну пешку. Найдите вероятность того, что пешка окажется белой.

Самостоятельная работа 2 по теме «Вероятности событий»

1. В случайном эксперименте 17 элементарных событий. Событию А бла­гоприятствуют 8 из них. Сколько элементарных событий благоприятствует событию ? Найдите вероятность события , если вероятность события А равна 0,32.

2. Бросают одну игральную кость. Событие А — выпало четное число очков. Событие В состоит в том, что выпало число очков, большее 3. Выпишите все элементарные события, благоприятствующие событию A UB. Найдите Р(АUB).

3. Бросают две игральные кости. Событие A — на первой кости выпало мень­ше 3 очков. Событие В — на второй кости выпало больше 4 очков. Выпишите элементарные события, благоприятствующие событию АВ. Опишите словами это событие и найдите его вероятность.

4. События U и V несовместны. Найдите вероятность их объединения, если P(U)= 0,3, Р(V) = 0,5.

Самостоятельная работа 3 по теме «Независимые события»

1. События U и V независимы. Найдите вероятность наступления события UV, если P(U) = 0,3, P(V) = 0,5.

2. События К и L независимы. Найдите вероятность события К, если P(L) = 0,9, Р(КL) = 0,72.

3. Монету бросают два раза. Выпишите все элементарные события этого эксперимента. Событие А — первый раз выпал орел. Событие В — второй раз выпала решка. Найдите вероятность каждого из этих событий и вероятность их пересечения. Являются ли эти события независимыми?

4. Из ящика, где хранятся 5 желтых и 7 красных карандашей, продавец, не глядя, вынимает один за другим 3 карандаша. Найдите вероятность того, что:

а) все карандаши окажутся желтыми;

б) первые два карандаша — желтые, а третий — красный.

5*. Случайным образом выбирается натуральное число от 1 до 50. Событие С — выбрано четное число. Являются ли события С и D независимыми, если событие D состоит в том, что:

а) выбранное число делится на 7;

б) выбранное число делится на 5.

Самостоятельная работа 4 по теме

«Перестановки и факториал числа»

1. Домашнее задание по литературе состоит в том, чтобы выучить одно из трех стихотворений: «Анчар», «Буря» и «Вьюга». Миша, Никита и Олег решили распределить все три стихотворения между собой по одному. Сколько существует способов это сделать?

2. Сколько различных последовательностей (не обязательно осмысленных) можно составить из букв слова «книга»?

3. Вычислите значение выражения: а) 5!; б); в)

4. Найдите вероятность того, что три последние цифры случайно выбран­ного телефонного номера — это цифры 2, 3, 1 в произвольном порядке.

Самостоятельная работа 5 по теме «Сочетания»

1. Вычислите: а) ; б).

2. В классе 20 учеников. Учитель решил проверить домашнюю работу у 6 из них. Сколько существует способов выбрать учеников для проверки?

3. Найдите вероятность того, что все буквы «а» окажутся на своих местах, если случайным образом перемешать и выстроить в ряд все буквы слова «ка­рандаш».

4. На книжной полке 6 учебников и 3 сборника стихов. Найдите вероятность того, что среди случайно выбранных 5 книг окажется 3 учебника и 2 сборника.

Примерная контрольная работа

Вариант 1

1. В барабане лотереи 20 одинаковых шаров. Шары пронумерованы от 1 до 20. Барабан вращается, и из него выпадает один шар. Найдите вероятность того, что номер шара — четное число.

2. В результате некоторого опыта с вероятностью 0,63 может наступить со­бытие A, с вероятностью 0,59 —событие В и с вероятностью 0,22 —событие

А В. Найдите вероятность события A U В. Является ли событие A U В досто­верным?

3. Игральную кость бросают дважды. Найдите вероятность того, что в пер­вый раз выпадет четное число, а во второй — число, большее чем 3.

4. В экзамене 6 вопросов. К каждому вопросу дано 2 варианта ответов, из которых только один вариант верный. Найдите вероятность того, что, отвечая наугад, ученик правильно ответит хотя бы на один вопрос.

5. В кармане у Буратино 5 золотых и 6 серебряных монет. Все монеты одинаковы по форме и размеру. Буратино, не глядя, вынимает из кармана 5 монет. Найдите вероятность того, что все эти монеты — золотые.

Вариант 2

1. Слово «Математика» написали на картонке и разрезали картонку на бук­вы. Буквы перемешали. Найдите вероятность вытащить наудачу картонку с гласной буквой.

2. В результате некоторого опыта с вероятностью 0,78 может наступить событие А, с вероятностью 0,34 —событие В и с вероятностью 0,11 —собы­тие AB. Найдите вероятность события AUB? Верно ли, что событие AUB достоверное?

3. Игральную кость бросают дважды. Найдите вероятность того, что в пер­вый раз выпадет нечетное число, а во второй — число, меньшее чем 3.

4. В экзамене 5 вопросов. К каждому вопросу дано 2 варианта ответов, из которых только один вариант верный. Найдите вероятность того, что, отвечая наугад, ученик даст хотя бы один неверный ответ.

5. В вазочке на шкафу 4 конфеты с фруктовой начинкой и 5— с молочной. Все конфеты одинаковы по форме и размеру. Маша дотянулась рукой до вазочки и, не глядя, выбирает 5 конфет. Найдите вероятность того, что все выбранные конфеты имеют молочную начинку.

9 класс

Самостоятельная работа 1 по теме «Геометрическая вероятность»

1. В отрезке ВС случайным образом выбирается точка А. Найдите вероят­ность того, что эта точка принадлежит отрезку ОМ, где О — середина отрезка ВС, а M — середина отрезка ОВ.

2. Из числового отрезка [2; 5] наудачу выбираются точки х и у. Найдите вероятность того, что х 3, а у 4.

3. На прямоугольном листе бумаги размером 10 см на 20 см нарисован квадрат. На лист бумаги случайным образом ставится точка. Вероятность того, что эта точка окажется внутри квадрата, равна 0,08. Найдите длину стороны нарисованного квадрата.

4*. В треугольнике ABC с тупым углом В случайным образом выбирается точка М. Точка D — середина высоты ВН. Найдите вероятность того, что эта точка принадлежит:

а) треугольнику ADC ; б) треугольнику ABD .

Самостоятельная работа 2 по теме «Испытания Бернулли»

1. Проводится серия из 6 независимых испытаний Бернулли с вероятно­стью успеха р = . Найдите вероятность элементарного события, в котором

наступает сначала 2 успеха, а затем —4 неудачи.

2. Сколько элементарных событий с 4 успехами возможно в серии из 10 испытаний Бернулли?

3. Найдите вероятность выбросить ровно 6 орлов, 10 раз бросив монету.

4*. Стрелок стреляет в мишень. Вероятность попадания равна 0,4. Найдите

вероятность того, что, сделав 5 выстрелов, стрелок попадет в мишень не менее 2 раз.

Самостоятельная работа 3 по теме «Распределение случайной величины»

1. Случайная величина принимает все четные значения от —2 до 6 с рав­ными вероятностями. Постройте таблицу распределения вероятностей этой случайной величины.

2. Пять человек выстраиваются в очередь случайным образом. Среди этих пятерых в очереди стоит Иван Иванович. Постройте распределение случайной величины «число людей в очереди, стоящих перед Иваном Ивановичем».

3. В таблице дано распределение некоторой случайной величины X . Най­дите пропущенную вероятность.

Значение

1

2

3

4

5

6

7

8

Вероятность

0,16

0,2

0,03

0,05

0,12

0,07

0,24

4*. Случайная величина Z принимает натуральные значения от 1 до 6 с вероятностями P(Z = к) = Найдите значение а.

Самостоятельная работа 4 по теме

«Математическое ожидание и дисперсия»

1. Случайная величина принимает все нечетные значения от —3 до 5 с равными вероятностями. Найдите ее математическое ожидание.

2. В таблице дано распределение случайной величины X . Чему равно Е(Х)?

Значение

1

2

3

4

5

6

7

8

Вероятность

0,16

0,19

0,02

0,06

0,11

0,06

0,15

0,25

3. Игральную кость бросили 64 раза. Найдите математическое ожидание, дисперсию и стандартное отклонение случайной величины X, равной числу выпадения четного числа очков.

4*. Серию испытаний Бернулли проводят дважды. В первый раз вероятность успеха была равна , а во второй раз вероятность успеха равнялась

В обоих случаях случайная величина S —число наступивших успехов. В каком из случаев ожидаемый разброс величины S больше?

Примерная контрольная работа

Вариант 1

1. Найдите вероятность наступления ровно 3 успехов в 8 испытаниях Бернулли с вероятностью успеха р =.

2. В таблице дано распределение случайной величины X . Чему равна про­пущенная вероятность?

Значение

1

2

3

4

5

6

Вероятность

0.16

0.29

0.16

0,21

0,06

3. Игральную кость бросают один раз. Найдите математическое ожидание случайной величины «сумма кубов числа выпавших очков».

4. Игральную кость бросили 120 раз. Найдите математическое ожидание и дисперсию случайной величины «число выпадений четверки».

5*. В квадрат со стороной 1 дм вписан круг. Из квадрата случайным образом выбираются две точки. Найдите вероятность того, что обе точки принадлежат кругу.

Вариант 2

1. Найдите вероятность наступления ровно 4 успехов в 9 испытаниях Бернулли с вероятностью неудачи q = .

2. В таблице дано распределение случайной величины X . Чему равна про­пущенная вероятность?

Значение

-3

-2

-1

1

2

3

Вероятность

0,17

0,28

0,1

0,19

0,08

3. Игральную кость бросают один раз. Найдите математическое ожидание случайной величины «сумма квадратов числа выпавших очков».

4. Игральную кость бросили 180 раз. Найдите математическое ожидание и дисперсию случайной величины «число выпадений двойки».

5*. В круг радиусом 1 дм вписан квадрат. Из круга случайным образом выбираются две точки. Найдите вероятность того, что обе точки принадлежат квадрату.

V . СЛОВАРЬ ТЕРМИНОВ

Баррель (от слова «бочка») — единица объема, принятая для нефти; при­мерно 159 литров.

Бином Ньютона — формула для возведения в п-ю степень двучлена (бино­ма) a + b:

= + + + ... +

Название формула получила в честь великого английского математика сэра Исаака Ньютона, который обобщил ее на случай дробных и отрицательных показателей степени.

Биномиальные коэффициенты — коэффициенты в формуле бинома Нью­тона. Каждый коэффициент является числом сочетаний из п по к.

Благоприятствующее элементарное событие. Элементарное событие, при наступлении которого наступает событие А, называется элементарным событием, благоприятствующим событию А.

Вероятность — числовая мера правдоподобия события. Вероятность прини­мает значения от 0 до 1.

Выбор наудачу (случайный выбор) — выбор одного предмета из некото­рого набора, при котором шансы на выбор любого предмета одинаковы.

Выборка — часть всей совокупности людей или предметов, отобранная для исследования. Например, выборкой является группа избирателей, которую опрашивают для предварительного выяснения шансов кандидатов на избрание в парламент страны.

Демография — наука о закономерностях изменения численности и состава населения.

Диаграмма — метод графического представления данных, который исполь­зуется для наглядного их отображения и сравнения. Как правило, диаграммы не дают точных значений, но лишь приблизительные.

Диаграмма круговая — диаграмма в виде круга, разделенного на секто­ры. Каждый сектор показывает, какую долю целого составляет та или иная величина в наборе данных. Обычно круговые диаграммы применяются для изображения состава населения, деления экономики на отрасли и т. п.

Диаграмма рассеивания — диаграмма, составленная из точек на коорди­натной плоскости. Диаграммы рассеивания применяются для изучения связей между различными характеристиками, например ростом и весом животного и т. д. Абсцисса и ордината каждой точки — значения этих характеристик.

Диаграмма столбиковая — диаграмма, наглядно показывающая соотноше­ние между различными значениями. Каждое значение представляется в виде столбика, высота которого пропорциональна этому значению.

Диаграмма Эйлера — способ графического изображения событий в виде фигур на плоскости. Каждое событие изображается некоторой фигурой, пере­сечение событий — общей частью этих фигур, объединение событий — объеди­нением фигур. Диаграммы Эйлера позволяют наглядно показать связь между различными событиями. Несовместные события изображаются фигурами, не имеющими общих точек.

Дисперсия случайной величины — мера рассеивания (разброса) значений случайной величины, определяемая формулой

D(X) = E(X - E(X))2 .

Дисперсию также можно вычислять по формуле

D(X) = E(X2 ) - E2 (X).

У постоянной случайной величины дисперсия равна нулю.

Дисперсия набора чисел — мера разброса значений числовых наборов (чи­словой выборки). Дисперсия набора равна среднему квадрату отклонения чисел набора от среднего арифметического значения:

=

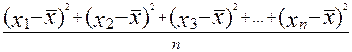
Достоверное событие — событие, вероятность которого равна 1. Это собы­тие обязательно происходит при проведении опыта. Примером достоверного события является событие «выпал либо орел, либо решка» при бросании мо­неты.

Событие, противоположное достоверному, называется невозможным.

Дюйм — мера длины, равная 2,54 сантиметра. Один фут состоит из 12 дюй­мов. Один дюйм равен 10 линиям. В дюймах и линиях, например, измеряется калибр оружия. Знаменитая винтовка Мосина называется трехлинейкой, по­скольку имеет калибр 3 линии, т. е. 7,62 мм. Трехдюймовка—орудие, имеющее калибр три дюйма — 76,2 мм.

Футы и дюймы — основные единицы измерения роста людей, длин и высот сооружений в США.

Закон больших чисел — собирательное название группы математических теорем, утверждающих, что среднее значение суммы случайных величин мало отличается от среднего значения их математических ожиданий при различных условиях. Основное условие — большое число складываемых величин, откуда и происходит название закона.

Испытание Бернулли— эксперимент, который заканчивается одним из двух элементарных событий: успехом или неудачей.

Комбинаторная задача — задача, связанная с необходимостью перечисле­ния предметов или их комбинаций.

Легенда диаграммы — изображение условных обозначений с разъяснения­ми. Легенды также бывают у географических карт.

Маловероятное событие — событие, вероятность которого в обычных усло­виях считается малой. Пример — выигрыш в лотерею.

Математическая монета — «идеальная» монета, которая падает вверх орлом с вероятностью . Все свойства настоящей монеты — размер, материал, достоинство — для математической монеты несущественны. Математическую монету еще называют симметричной монетой.

Математическая игральная кость — «идеальный» игральный кубик, для

которого вероятность выпадения любой грани равна . Математическую кость называют также симметричной. Наилучшим приближением к математической кости является обычная правильная кость.

Математическое ожидание случайной величины — числовая характери­стика случайной величины, показывающая ее среднее значение. Математиче­ское ожидание случайной величины вычисляется по формуле

Е(Х) =+ + ...+,

где — вероятность того, что X = .

Медиана числового набора. Медиана набора — число, которое характери­зует расположение набора на числовой прямой.

Чтобы найти медиану, набор чисел можно упорядочить по возрастанию. Если в полученном наборе нечетное количество чисел, то медиана —это число, стоящее посередине; если в полученном наборе четное количество чисел, то медиана равна полусумме двух чисел, стоящих посередине.

Мера рассеивания (мера разброса) — числовая характеристика, показы­вающая, насколько близко к среднему значению группируются числа в наборе или значения случайной величины. Наиболее употребительные меры рассеива­ния — размах набора, средний модуль отклонения, дисперсия (средний квадрат отклонения) и стандартное отклонение (арифметический квадратный корень из дисперсии).

Наибольшее значение набора — число в наборе, которое не меньше, чем любое другое число этого набора.

Наименьшее значение набора — число в наборе, которое не больше, чем любое другое число этого набора.

Невозможное событие — событие, вероятность которого в данном опыте равна нулю. Невозможное событие противоположно достоверному.

Независимые события. Два события А и В называются независимыми, если вероятность их пересечения равна произведению их вероятностей:

Р(АВ)=Р(А)-Р(В).

Часто независимость событий объясняется независимостью опытов, к ко­торым они относятся. Например, независимы два события, относящиеся к различным испытаниям Бернулли.

Независимые случайные величины. Если любые два события, одно из которых связано со случайной величиной X , а другое — со случайной величи­ной Y , независимы, то случайные величины X и Y называются независимыми.

Аналогично определяется произвольное количество независимых величин.

Важным примером независимых величин является число успехов в различ­ных независимых испытаниях Бернулли.

Для независимых случайных величин X и Y верны следующие свойства:

1) Е(ХУ) = Е(Х)-Е(У);

2) D(X + Y)=D(X)+D(Y).

Несовместные события — два события, которые не могут наступить в од­ном и том же опыте вместе (одновременно). Примером несовместных событий являются противоположные события.

Номинальный вес изделия — вес изделия, который должен получиться со­гласно технологии производства. Вес изделия при массовом производстве — величина изменчивая, поэтому для каждого изделия вес может немного отли­чаться от номинального.

Объединение (сумма) событий. Объединением событий А и В называется событие, которое происходит в том и только в том случае, когда происходит хотя бы одно из событий А и В.

Орел — одна из сторон монеты (реверс). Другая сторона (аверс) называется решкой. Выпадение орла —одно из двух элементарных событий при бросании монеты.

Отклонение стандартное (среднее квадратичное) — мера рассеивания, ко­торая равна арифметическому квадратному корню из дисперсии случайной величины:

=

Пересечение (произведение) событий. Пересечением событий А и В на­зывается событие, которое происходит в том и только в том случае, когда наступают оба события А и В.

Перестановка — один из способов нумерации элементов некоторого множества. Если в множестве п элементов, то существует п! перестановок этих элементов.

Правило сложения вероятностей — правило, по которому вычисляется вероятность объединения событий. Для двух произвольных событий А и В верна формула

Р (АUВ)=Р(А)+Р(В)-Р(АВ).

Если события А и В несовместны, то формула принимает более простой вид:

P(AUB)=P(A)+P(B).

Правило умножения вероятностей — правило, которое гласит, что

вероятность пересечения независимых событий равна произведению их вероятностей:

Р(АВ) = Р(А)Р(В).

Правило умножения комбинаторное — правило, которое гласит, что число пар из двух предметов двух типов равно

т n ,

где т — число предметов первого типа, п — число предметов второго типа. Имеется в виду, что в паре на первом месте стоит предмет первого типа, на втором - предмет второго типа.

Аналогично вычисляется число упорядоченных наборов, состоящих из предметов трех, четырех и более типов.

Противоположное событие. Событием, противоположным событию А называется событие , состоящее в том, что событие А не наступило. Можно сказать иначе: событие наступает тогда и только тогда, когда не наступает событие А.

Равновозможные элементарные события — элементарные события, у которых одинаковые шансы на наступление. Примером может служить опыт, состоящий в бросании правильной игральной кости. В этом опыте шесть элементарных событий, и все они равновозможны.

Равновероятные события — события, вероятности которых равны.

Приме ром равновероятных событий могут служить равновозможные элементарные события. В опыте с бросанием игральной кости вероятность каждого из элементарных событий равна , поэтому все они равновероятны.

Размах набора — разность между наибольшим и наименьшим значением этого набора.

Распределение вероятностей — закон, по которому каждому значению слу­чайной величины в соответствие ставится вероятность того, что величина при­мет это значение. Распределение для конечной случайной величины можно задать таблицей, диаграммой или формулой.

Решка — одна из сторон монеты (аверс). Другая сторона (реверс) называется орлом. Выпадение решки — одно из двух элементарных событий при бросании монеты.

Серия испытаний Бернулли — случайный эксперимент, состоящий в по­следовательном проведении нескольких отдельных независимых испытаний Бернулли с одной и той же вероятностью успеха.

Систематическая ошибка — одна и та же ошибка, возникающая при любом измерении или наблюдении и связанная с настройкой прибора. Например, если весы не отрегулированы, то они все время могут показывать на 10 г больше, чем надо. Здесь 10 г — систематическая ошибка.

Если систематической ошибки нет, то все другие отклонения связаны со случайной изменчивостью и называются случайными ошибками измерения.

Случайная величина— величина, которая принимает те или иные значения в ходе случайного опыта под воздействием случая.

Случайная изменчивость — способность некоторой величины принимать различные значения по воле случая, т. е. под воздействием различных обстоя­тельств, которые нет возможности ни предвидеть, ни изменить.

Случайное событие— событие, которое может наступить в ходе некоторого опыта, а может не наступить. Наступит случайное событие или нет — дело случая.

Случайный выбор — см. выбор наудачу.

Случайный опыт (случайный эксперимент) — математическая абстрак­ция, описывающая реальный опыт, который может оканчиваться различны­ми случайными событиями. Под случайным опытом можно также понимать наблюдение за некоторым явлением природы или измерение некоторой ве­личины (длины, массы и т. п.). Иногда случайный опыт проводят намерен­но. Примером может служить любая игра или лотерея, спортивное состя­зание.

Социологическое обследование — сбор информации об обществе с помо­щью опроса специально отобранной группы населения (выборки). Примером социологического обследования может служить предварительный опрос изби­рателей, тестирование учащихся или абитуриентов, изучение спроса и предло­жения товаров.

Сочетание. Любой набор к предметов, отобранных из набора, в котором п предметов, называется сочетанием из п по к.

Среднее набора чисел — среднее арифметическое чисел этого набора, т. е. их сумма, деленная на их количество.

Статистика — наука, посвященная методам систематизации, обработки и использования большого количества числовых данных. Такие данные назы­ваются статистическими. Важным примером статистических данных может служить численность групп населения страны, данные о производстве того или иного вида продукции, сведения о спросе и предложении какого-либо товара.

Теория вероятностей — раздел математики, изучающий вероятности собы­тий. Теория вероятностей разрабатывает методы, с помощью которых можно вычислить вероятности одних событий, зная вероятности других. Теория веро­ятностей изучает также случайные величины и их распределения.

Точность измерения. Под точностью измерения часто понимают допусти­мую ошибку, которую можно сделать при измерении. Например, измеряя рост человека, говорят об измерении с точностью до сантиметра.

Под точностью измерения также понимают разность между результатом измерения и истинным значением величины (длины, массы и т. п.).

Треугольник Паскаля (числовой или арифметический треугольник)—

тре­угольная таблица, в которой записаны биномиальные коэффициенты (числа сочетаний) . Крайние числа в каждой строке равны 1. Каждое число внутри треугольника получается сложением двух чисел, стоящих над ним. Треуголь­ник назван в честь французского математика Блеза Паскаля, опубликовавшего в 1665 году «Трактат об арифметическом треугольнике».

Урожайность зерновых культур — масса зерновых культур, собранных с одного гектара. Урожайность зерновых является важной характеристикой со­стояния сельского хозяйства страны.

Факториал. Факториалом натурального числа п называется произведение всех натуральных чисел, не превосходящих п. Факториал числа п обозначает­ся n!.

Таким образом, для натурального п факториал вычисляется по формуле

n!=1234…n

Факториал нуля по определению полагают равным единице: 0! = 1.

Частота. Пусть при проведении п случайных опытов событие А наступило

к раз. Частотой события А называется отношение .

Число сочетаний. Число различных сочетаний из п по к обозначается Ск и вычисляется по формуле =

Число успехов в серии испытаний Бернулли. Вероятность того, что в результате серии из п испытаний Бернулли наступит ровно к успехов, равна

P(S = k)=

где р и q — соответственно вероятности успеха и неудачи.

Численность (объем) выборки — количество чисел, людей, предметов в исследуемой выборке.

Элементарное событие — простейшее событие, которое наступает в ре­зультате случайного опыта. Элементарное событие нельзя разложить на более простые.

Любое событие опыта состоит из некоторых элементарных событий в том смысле, что является их объединением. Еще говорят, что элементарное событие может благоприятствовать некоторому событию.

VII . СПИСОК ОСНОВНОЙ И ДОПОЛНИТЕЛЬНОЙ

ЛИТЕРАТУРЫ ПО КУРСУ «ТЕОРИЯ ВЕРОЯТНОСТЕЙ

И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА»

1. Бунимович Е.А. Вероятность и статистика.- 5-9 кл.:пособие для общеобразовательных учреждений – 4-е изд.- М.: Дрофа, 2006.- 159с.

2. Вентцель Е.С. Теория вероятностей.- 4-е изд. – М.: Наука,1969.

3. Виленкин Н.Я. Комбинаторика. – М.: Наука, 1969.

4. Виленкин Н.Я. Индукция. Комбинаторика. – М.: Просвещение, 1976.

5. Виленкин Н.Я. Потапов В.Г. Задачник-практикум по теории вероятностей с элементами комбинаторики и математической статистики: Учебное пособие для студентов-заочников IVкурса физико-математических факультетов педагогических институтов – М.: Просвещение, 1979.

6. Гнеденко Б.В. Математика в современном мире.- М.: Просвещение, 1980.

7. Гнеденко Б.В., Хинчин А.Я. Элементарное введение в теорию вероятностей.-6-е изд.- М.: Наука, 1964.

8. Ивашов-Мусатов О.С. Теория вероятностей и математическая статистика.- М.: Наука, 1979.

9. Кордемский Б.А. Математика изучает случайности.- М.: Просвещение, 1975.

10. Лютикас В.С.Факультативный курс по математике: Теория вероятностей: Учебное пособие для 9-11 кл. сред. Шк. – 3-е изд., перераб.- М.: Просвещение, 1990.

11. Макарычев Ю.Н., Миндюк Н.Г.. Алгебра: Элементы статистики и теории вероятностей: Учебное пособие для учащихся 7-9 классов общеобразовательных учреждений / Под редакцией

С. А. Теляковского. - М.: Просвещение, 2003 - 78 с.

12. Математика в современном мире: Сборник статей/Перевод с англ. Н.Г. Рычковой.-М.: Мир, 1967.

13. Мостеллер Ф. Пятьдесят занимательных вероятностных задач с решениями. - М.: Наука, 1975.

14. Мостеллер Ф., Рурке Р., Томас ДЖ. Вероятность. - М.: Мир, 1969.

15. Мордкович А.Г., СеменовП.В. События. Вероятности, статистическая обработка данных: Дополнительные параграфы к курсу алгебры 7-9 классов общеобразовательных учреждений. - Мнемозина, 2003. - 112 с.

16. Пойа Д. Математика и правдоподобные рассуждения.- М.: Наука, 1975.

17. Солодовников А.С. Теория вероятностей.- М.: Просвещение, 1978.

18. Студенецкая В.Н. Решение задач по статистике, комбинаторике и теории вероятностей. 7-9 классы. – Волгоград: Учитель, 2005. – 429 с.

19. Ткачёва М.В., ФёдороваН.Е. Элементы статистики и вероятность6 учебное пособие для 7-9 классов общеобразовательных учреждений. – м.: Просвещение, 2004. – 112 с.

20. Тюрин Ю.П., Макаров А.А., Высоцкий И.Р., Ященко И.В. Теория вероятностей и статистика.- М.: МЦНМО: АО «Московские учебники», 2004. – 256 с.

21. Тюрин Ю.П., Макаров А.А., Высоцкий И.Р., Ященко И.В. Теория вероятностей и статистика/Методическое пособие для учителя- М.: МЦНМО: МИОО, 2005. – 48 с.

Скачать архив с текстом документа