Теория вероятности и математическая статистика
СОДЕРЖАНИЕ: Классическое определение вероятности события. Способы вычисления наступления предполагаемого события. Построение многоугольника распределения. Поиск случайных величин с заданной плотностью распределения. Решение задач, связанных с темой вероятности.Федеральное агентство по образованию РФ
НОУ ВПО Международный университет бизнеса и новых технологий (академия)
Контрольная работа по теории организации и математической статистике
Вариант № 4
Выполнила: Спицина Н. Н.
Специальность: МН - 2
Задание 1
В коробке 12 зеленых, 5 красных, 6 синих карандашей. Из коробки наудачу берут три карандаша. Какова вероятность того, что все они будут синими? Рассмотреть случаи, когда карандаши: а) не возвращают в коробку; б) возвращают в коробку.
Решение:
а) Событие А – все три вынутые без возращения в коробку карандаши синие.
Согласно классическому определению вероятность события А равна:
![]()
В коробке 12+5+6=23 карандаша.
Общее число исходов равно:
![]()
Благоприятное число способов равно:
![]()
![]()
Ответ: вероятность того, что все три вынутые без возращения в коробку карандаши синие, равна 0,011.
б) Событие В – все три вынутые с возращением в коробку карандаши синие, то есть три раза будут выниматься 1 синий шар из 23.
Вероятность извлечения одного синего карандаша р = 6/23.
Воспользуемся схемой Бернулли:
![]()
q = 1-6/23=7/23
n = 3
m=3
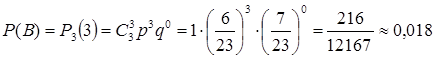
Ответ: вероятность того, что все три вынутые с возращения в коробку карандаши синие, равна 0,018.
Задание 2
Из колоды в 32 карты наугад вынимают 5. Найти вероятность того, что среди них окажется ровно один туз.
Решение:
Событие А – из вынутых наугад 5 карт, ровно один туз.
Согласно классическому определению вероятность события А равна:
![]()
Пусть детали пронумерованы с 1 до 80, с 1 до 20 стандартные и с 21 по 80 не стандартные.
Общее число исходов равно:
![]()
Благоприятное исход состоит в том, что вынут 1 туз из 4-х возможных и 4 другие карты из оставшихся 28, таким образом, число благоприятных способов равно:
![]()
![]()
Ответ: вероятность того, что из вынутых наугад 5 карт, ровно один туз, равна 0,407.
Задание 3
Брак изделий цеха составляет 11%. Найти вероятность того, что из 250 изделий цеха окажется бракованными: а) ровно 45 изделий; б) от 145 до 155 изделий; в) не менее 101 изделий; г) не более 100 изделий.
Решение:
а) Вероятность того, что из 250 изделий цеха окажется бракованными ровно 45 изделий, найдем, используя локальную теорему Лапласа:
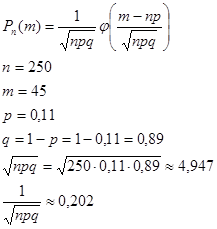
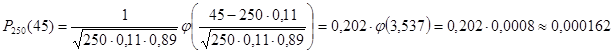
б) Вероятность того, что из 250 изделий цеха окажется бракованными от 145 до 155 изделий, найдем, используя интегральную теорему Лапласа:
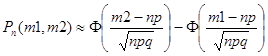
где Ф – функция Лапласа (значения берутся из таблиц).
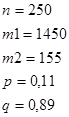
Подставляем:
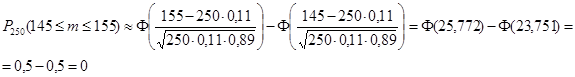
в) Вероятность того, что из 250 изделий цеха окажется бракованными не менее 101 изделий, найдем, используя интегральную теорему Лапласа:
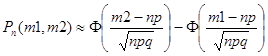 ,
,
где Ф – функция Лапласа (значения берутся из таблиц).
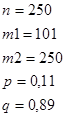
Подставляем:
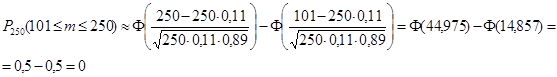
г) Вероятность того, что из 250 изделий цеха окажется бракованными не более 100 изделий, найдем, используя интегральную теорему Лапласа:
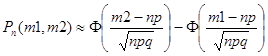
где Ф – функция Лапласа (значения берутся из таблиц).
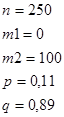
Подставляем:
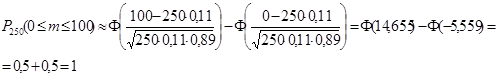
Задание 4
Радист трижды вызывает корреспондента. Вероятность того, что будет принят первый вызов, равна 0,2, второй вызов – 0,3, третий вызов 0,4. События, состоящие в том, что данный вызов будет услышан, независимы. Найти вероятность того, что корреспондент вообще услышит вызов.
Решение:
Событие А - корреспондент услышал вызов.
Событие Н1 - принят первый вызов.
Событие Н2 - принят второй вызов.
Событие Н3 - принят третий вызов.
Р( Н1 ) = 0,2, Р( Н2 ) = 0,3, Р( Н3 ) = 0,4.
Р (А / Н1) = 1/3; Р (А / Н2) = 1/3; Р( А/Н2 ) = 1/3.
Используя формулу полной вероятности, получим
Р( А ) = Р( А / Н1 ) · Р( Н1 ) + Р( А / Н2 ) · Р( Н2 ) + Р( А / Н3 ) · Р( Н3 ) =
![]()
Ответ: вероятность того, что корреспондент услышал вызов, равна 0,3.
Задание 5
Случайная величина имеет распределение вероятностей, представленное таблицей:
| 1 | 2 | 3 | 4 | 5 | |
| Р(Х) | 0,1 | 0,15 | 0,2 | 0,3 |
Найти Р(3), функцию распределения F(Х). Построить многоугольник распределения.
Решение:
Найдем Р(3):
![]()
![]()
![]()
| 1 | 2 | 3 | 4 | 5 | |
| Р(Х) | 0,1 | 0,15 | 0,25 | 0,2 | 0,3 |
Найдем и построим функцию распределения F(Х):
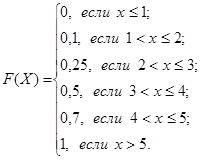
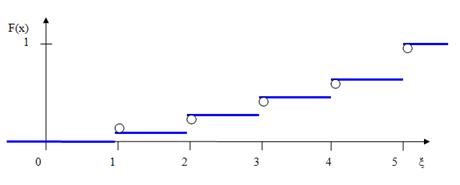
Построим многоугольник распределения:
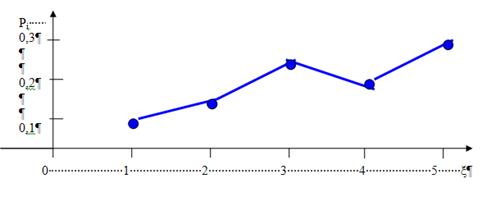
Задание 6
Найти М(), D(), () случайной величины примера 5.
Решение:
Найдем М() случайной величины из примера 5:
![]()
Найдем D() случайной величины из примера 5:
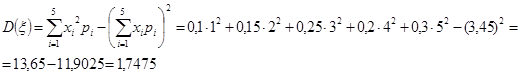
Найдем ![]() случайной величины из примера 5:
случайной величины из примера 5:
![]()
Задание 7
- непрерывная случайная величина с плотностью распределения (Х), заданной следующим образом:
(Х)= ![]()
Найти функцию распределения F(Х).
Решение:
Найдем функцию распределения F(Х):
При ![]()
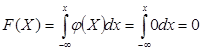
При ![]()
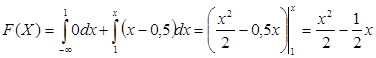
При ![]()
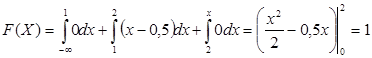
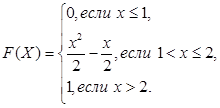
Задание 8
- непрерывная случайная величина из примера 7. Найти М(), D().
Решение:
Найдем М():
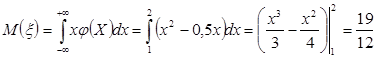 .
.
Найдем D():